写题遇到的一些树上操作
《在树上找到每一个节点的各个子树的节点个数》
实现的时间复杂度O(n),n为节点个数
原题链接:https://codeforces.com/gym/103736/problem/D
以这张图为例:在3节点上其子树的节点个数分别为1 1 2;
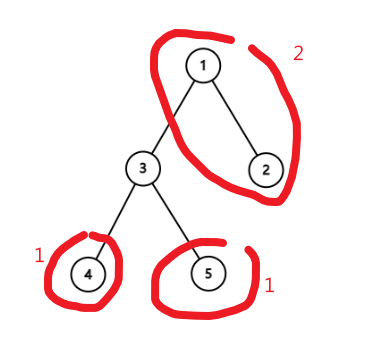
算法实现:
首先设计一个dfs函数:int dfs(int x,int f)
其含义为:找到以x为根时,而且x的父节点为f时,其全部子树的节点个数(包含自己)
1 // cNum[i]:记录以i为根其各个子树的大小
2 vector<int> cNum[N];
3 // sum[i]:记录以1为根,在i为根的时候,其子树+自身的节点个数
4 int sum[N];
5 void dfs(int s, int fa)
6 {
7 sum[s]++;
8 for (int i = 0; i < sides[s].size(); i++)
9 {
10 int child = sides[s][i];
11 if (child == fa)
12 continue;
13 dfs(child, s);
14 cNum[s].push_back(sum[child]);
15 sum[s] += sum[child];
16 }
17 if (n - sum[s] != 0)
18 cNum[s].push_back(n - sum[s]);
19 }
算法关键:
你肯定会想:以这种递归的方式调用下去,不是只会找到其下面的子树节点个数,其以前的父节点存在的子树不会进行查找
但是如果我们找到了全部的下面的子树节点个数,然后用n-全部的下面的子树节点个数-1
就为以前的父节点存在的子树的节点个数,即为如下这一步:

《树上的Dijkstra思想》
原题链接:https://codeforces.com/gym/401803/problem/B
简单翻译一下为:
特雷兰是一个由n个城市和n个−1条双向道路。正如你所想象的那样,特里兰是一棵树,这意味着每对城市之间只有一条简单的道路。
Treeland总统计划在n天内在该国建立一个5G网络。每天,将根据以下规则在不同的城市建造5G天线塔:
1 .每天,必须在距离已建成天线的城市不超过k的城市建造天线。此限制不适用于第一天。
2. 如果在第i天有多个有效城市可以建造天线,则必须选择数量最少的城市。
即按照最小字典输出建造城市顺序的编号

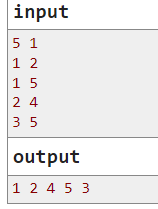
很显然,为了字典序最小,编号为1的城市为第一个建造的城市
然后以1城市为最新点,去更新能够到的城市,然后从其中找到全部能够到的城市的编号最小的城市
算法实现:
首先,用优先队列pq,将能够到的城市装进pq中,然后从pq中取出编号最小的点
以这个点为起点,继续更新能够到的城市
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 #include <vector>
5 #include <queue>
6 using namespace std;
7 const int N = 1e5 + 2;
8 vector<int> ans;
9 priority_queue<int, vector<int>, greater<int>> pq;
10 vector<int> sides[N];
11 int n, k;
12 int vis[N];
13 void bfs(int s)
14 {
15 queue<int> q;
16 q.push(s);
17 vis[s] = 0;
18 while (q.size())
19 {
20 int x = q.front();
21 q.pop();
22 if (vis[x] >= k)
23 continue;
24 for (int i = 0; i < sides[x].size(); i++)
25 {
26 int node = sides[x][i];
27 if (vis[node] == -1)
28 {
29 vis[node] = vis[x] + 1;
30 q.push(node);
31 pq.push(node);
32 }
33 else if (vis[node] >= vis[x] + 1)
34 {
35 vis[node] = vis[x] + 1;
36 q.push(node);
37 }
38 }
39 }
40 }
41 int main()
42 {
43 cin >> n >> k;
44 for (int i = 1; i <= n - 1; i++)
45 {
46 int a, b;
47 scanf("%d%d", &a, &b);
48 sides[a].push_back(b), sides[b].push_back(a);
49 }
50 memset(vis, -1, sizeof(vis));
51 pq.push(1);
52 while (pq.size())
53 {
54 int x = pq.top();
55 pq.pop();
56 ans.push_back(x);
57 bfs(x);
58 }
59 for (int i = 0; i < ans.size(); i++)
60 cout << ans[i] << " ";
61 return 0;
62 }
算法关键:
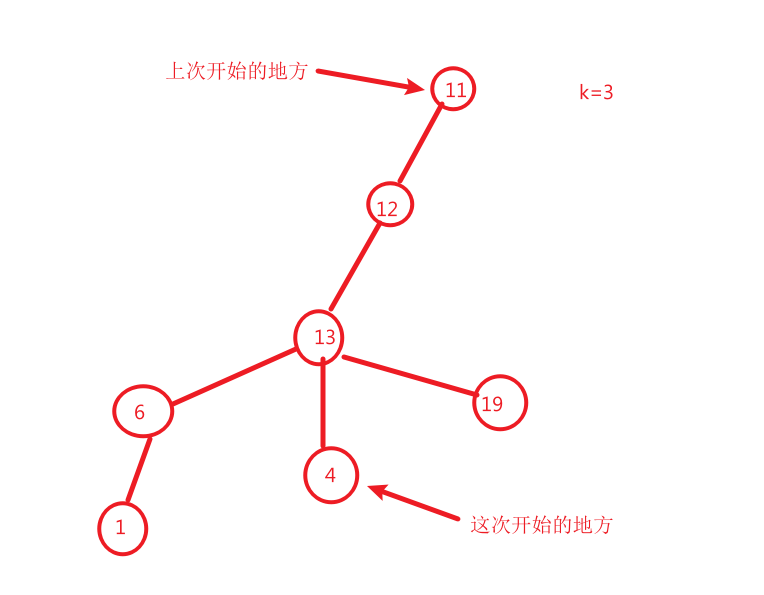
上次从点11开始,然后扩展点
然后,下一次到了点4开始,注意这一次vis是给点13,点6,点19都打上了标记,
但是如果我们在bfs()如果看到了vis标记过了的就不去看会有大问题
比如这个案例中:
点1是上次在点11是无法扩展到的,但是在点4就可以扩展到
如果我们看到了vis标记过了的就不去看,那么在点4,点1就无法扩展了
解决方案:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号