最小生成树
《不能使用最小生成树的情况》
在没有说不能产生回路时:

这个情况是不能使用最小生成树算法的,因为边可以是负的,如果再加上一条边,这条边是负的,正好还可以减少权重
《Kruskal算法的大用》
用kruskal算法就像用一个进度条求最小生成树一样,即如果在开始时,最小生成树已经完成了一部分,可以用
kruskal算法继续完成,或者有些必要条件必须选边用这个算法更加方便,如:

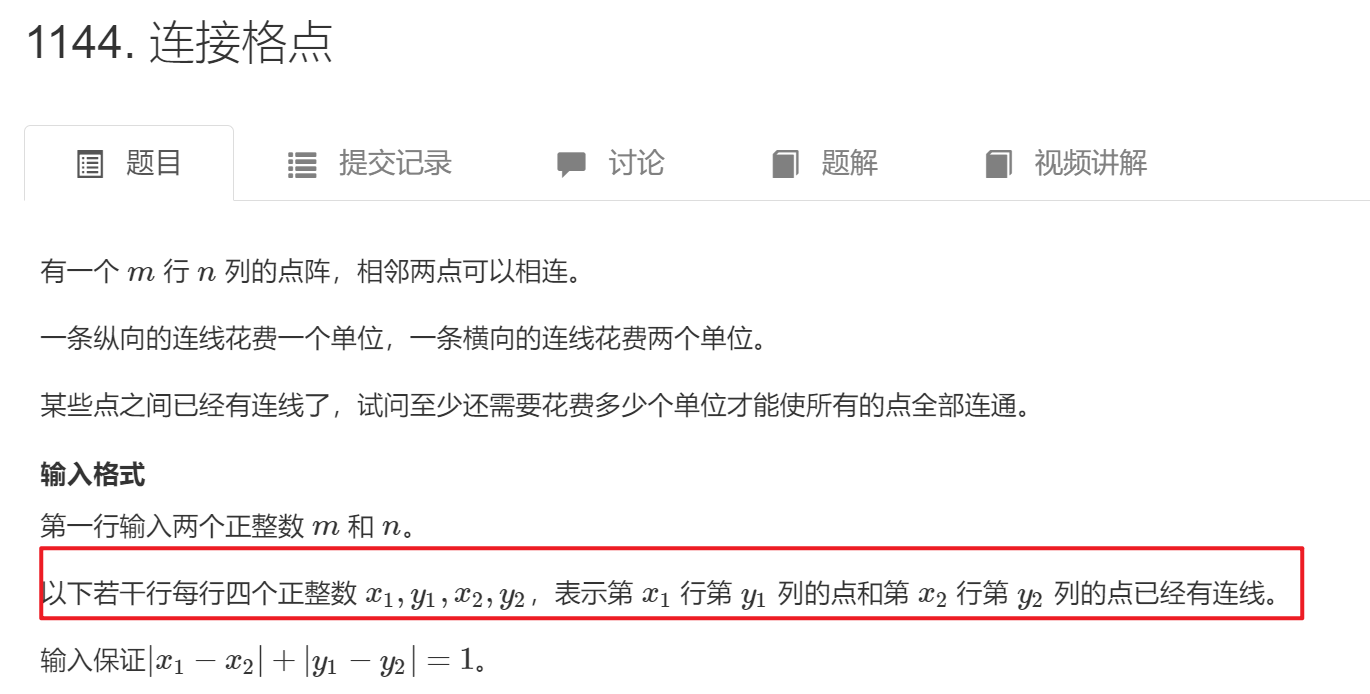
连接格点这道题,如果像平常使用kruskal算法包含sort会超时,
那我们可以在建图的时候就按照边权小的先建
1 #include<bits/stdc++.h>
2 #define N 1010
3 using namespace std;
4 int n,m;
5 int fa[N*N],tot;
6 int find(int x)//并查集基本操作
7 {
8 if(fa[x]==x)
9 return x;
10 return fa[x]=find(fa[x]);
11 }
12 inline int merge(int x,int y)//并查集基本操作
13 {
14 int fa_x=find(x);
15 int fa_y=find(y);
16 if(fa_x!=fa_y){
17 fa[fa_y]=fa_x;
18 return 1;//已经连了一条边
19 }
20 return 0;
21 }
22 int main()
23 {
24 scanf("%d %d",&n,&m);
25 for(int i=1;i<=n*m;i++)//并查集初始化
26 fa[i]=i;
27 int x1,y1,x2,y2;
28 while(~scanf("%d %d %d %d",&x1,&y1,&x2,&y2)){
29 int u=(x1-1)*m+y1,v=(x2-1)*m+y2;//转换为对应的编号
30 merge(u,v);//合并
31 }
32 for(int i=1;i<=m;i++)//竖向合并一遍
33 for(int j=1;j<n;j++){
34 int u=(j-1)*m+i,v=j*m+i;//坐标转换
35 if(merge(u,v))//当前两点有一条边连接
36 tot++;//竖向答案+1
37 }
38 for(int i=1;i<=n;i++)//横向合并一遍
39 for(int j=1;j<m;j++){
40 int u=(i-1)*m+j,v=(i-1)*m+j+1;//坐标转换
41 if(merge(u,v))//当前两点有一条边连接
42 tot+=2;//横向答案+2
43 }
44 printf("%d\n",tot);
45 return 0;
46 }
《kruskal算法与连通块之间的关系》
因为并查集本身在建树的过程就是连通块不断减少的过程,最终使只剩下一个连通块
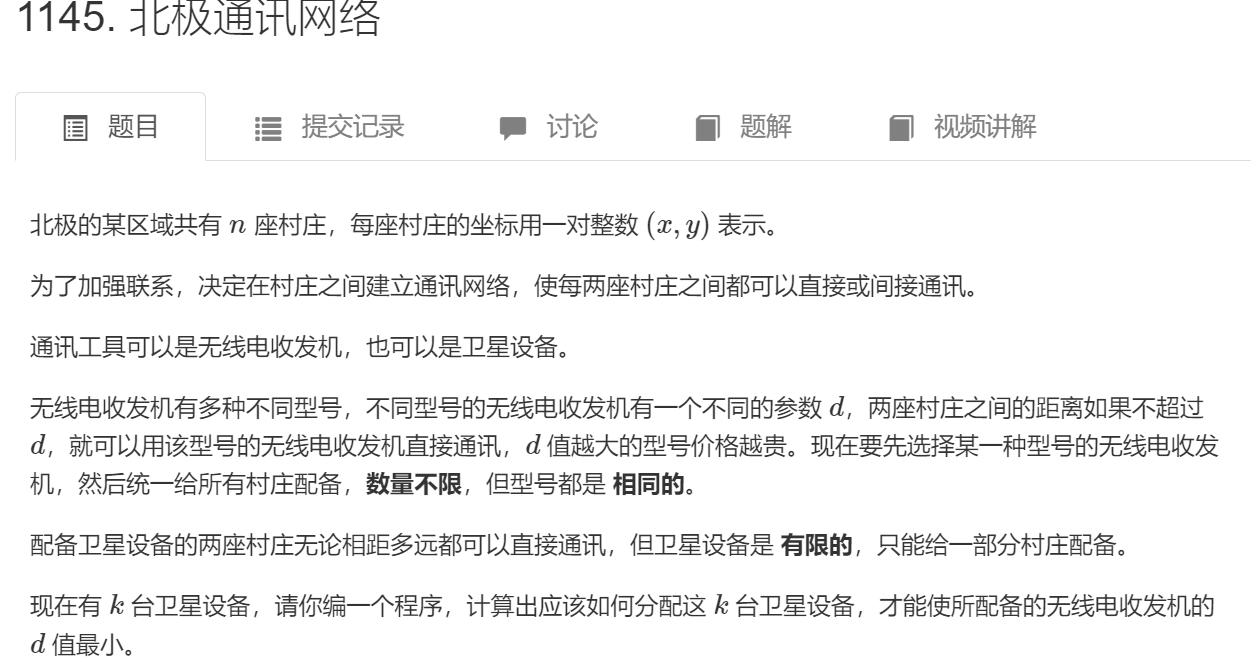

我的错误思想:先做一遍最短路,然后将最短路中的边排序,将最大边相连的点用卫星连起来
,但是这个思想是错误的,因为我没有考虑到一旦有点用卫星连起来,这些点之间权重就全部变成了0
之前作的最短路就明显不对了
正确思路:
模型抽象:选择最小的d,去除点之间大于d的路径,然后能够使连通块的数量<=k
很明显,d与连通块的数量之间有这样的关系:
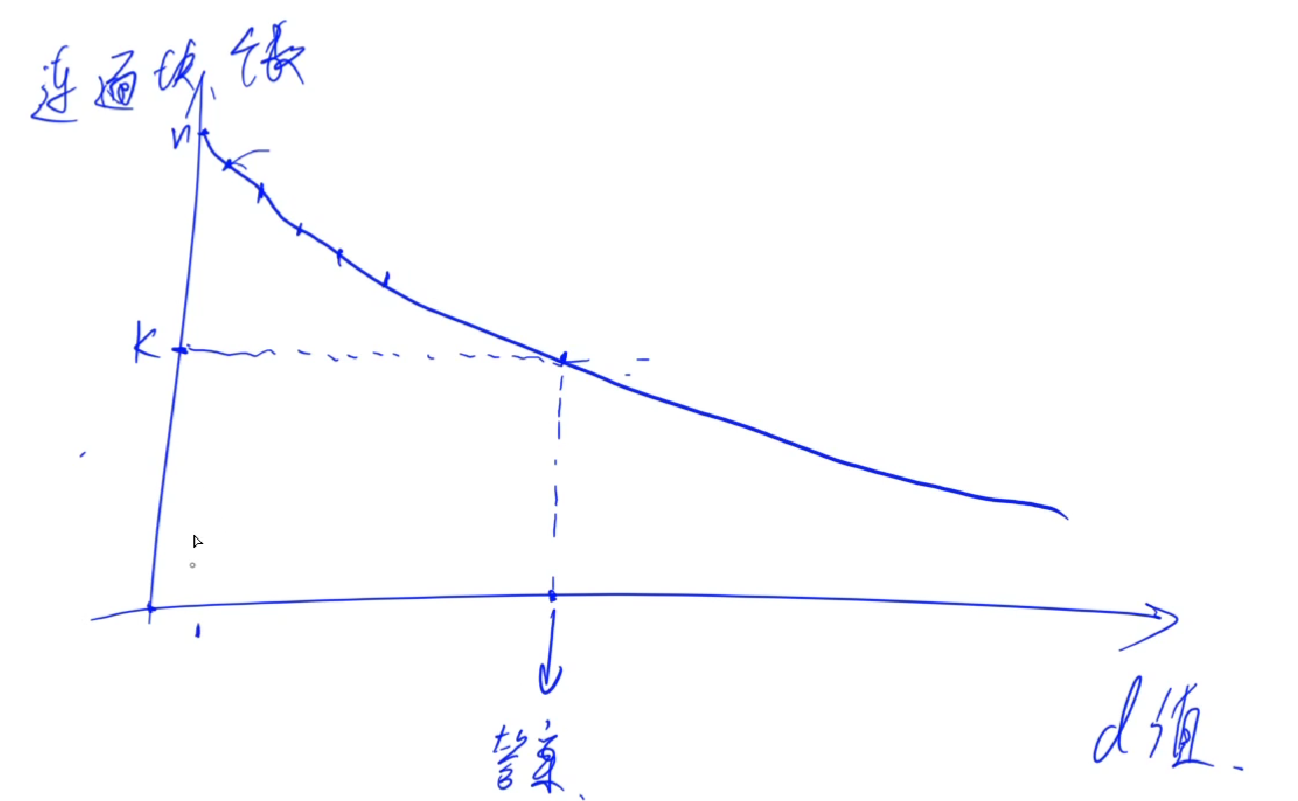
按照正常的kruskal算法,当我们使用sides[]的w时,其实就是<=w的边全部已经建好,>w的边还没有用的建立连通块的情况
我们只要找到一个sides[]的w,使;连通块的数第一次<=k

1 #include <cstring> 2 #include <iostream> 3 #include <algorithm> 4 #include <cmath> 5 6 #define x first 7 #define y second 8 9 using namespace std; 10 11 typedef pair<int, int> PII; 12 13 const int N = 510, M = N * N / 2; 14 15 int n, k, m; 16 struct Edge 17 { 18 int a, b; 19 double w; 20 bool operator< (const Edge &t) const 21 { 22 return w < t.w; 23 } 24 }e[M]; 25 PII q[M]; 26 int p[N]; 27 28 double get_dist(PII a, PII b) 29 { 30 int dx = a.x - b.x; 31 int dy = a.y - b.y; 32 return sqrt(dx * dx + dy * dy); 33 } 34 35 int find(int x) 36 { 37 if (p[x] != x) p[x] = find(p[x]); 38 return p[x]; 39 } 40 41 int main() 42 { 43 cin >> n >> k; 44 for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y; 45 for (int i = 0; i < n; i ++ ) 46 for (int j = 0; j < i; j ++ ) 47 e[m ++ ] = {i, j, get_dist(q[i], q[j])}; 48 49 sort(e, e + m); 50 for (int i = 0; i < n; i ++ ) p[i] = i; 51 52 int cnt = n; 53 double res = 0; 54 for (int i = 0; i < m; i ++ ) 55 { 56 if (cnt <= k) break; 57 58 int a = find(e[i].a), b = find(e[i].b); 59 double w = e[i].w; 60 if (a != b) 61 { 62 p[a] = b; 63 cnt -- ; 64 res = w; 65 } 66 } 67 68 printf("%.2lf\n", res); 69 70 return 0; 71 } 72 73 作者:yxc 74 链接:https://www.acwing.com/activity/content/code/content/151271/ 75 来源:AcWing 76 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1 #include <cstring>
2 #include <iostream>
3 #include <algorithm>
4 #include <cmath>
5
6 #define x first
7 #define y second
8
9 using namespace std;
10
11 typedef pair<int, int> PII;
12
13 const int N = 510, M = N * N / 2;
14
15 int n, k, m;
16 struct Edge
17 {
18 int a, b;
19 double w;
20 bool operator< (const Edge &t) const
21 {
22 return w < t.w;
23 }
24 }e[M];
25 PII q[M];
26 int p[N];
27
28 double get_dist(PII a, PII b)
29 {
30 int dx = a.x - b.x;
31 int dy = a.y - b.y;
32 return sqrt(dx * dx + dy * dy);
33 }
34
35 int find(int x)
36 {
37 if (p[x] != x) p[x] = find(p[x]);
38 return p[x];
39 }
40
41 int main()
42 {
43 cin >> n >> k;
44 for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;
45 for (int i = 0; i < n; i ++ )
46 for (int j = 0; j < i; j ++ )
47 e[m ++ ] = {i, j, get_dist(q[i], q[j])};
48
49 sort(e, e + m);
50 for (int i = 0; i < n; i ++ ) p[i] = i;
51
52 int cnt = n;
53 double res = 0;
54 for (int i = 0; i < m; i ++ )
55 {
56 if (cnt <= k) break;
57
58 int a = find(e[i].a), b = find(e[i].b);
59 double w = e[i].w;
60 if (a != b)
61 {
62 p[a] = b;
63 cnt -- ;
64 res = w;
65 }
66 }
67
68 printf("%.2lf\n", res);
69
70 return 0;
71 }
72
73 作者:yxc
74 链接:https://www.acwing.com/activity/content/code/content/151271/
75 来源:AcWing
76 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
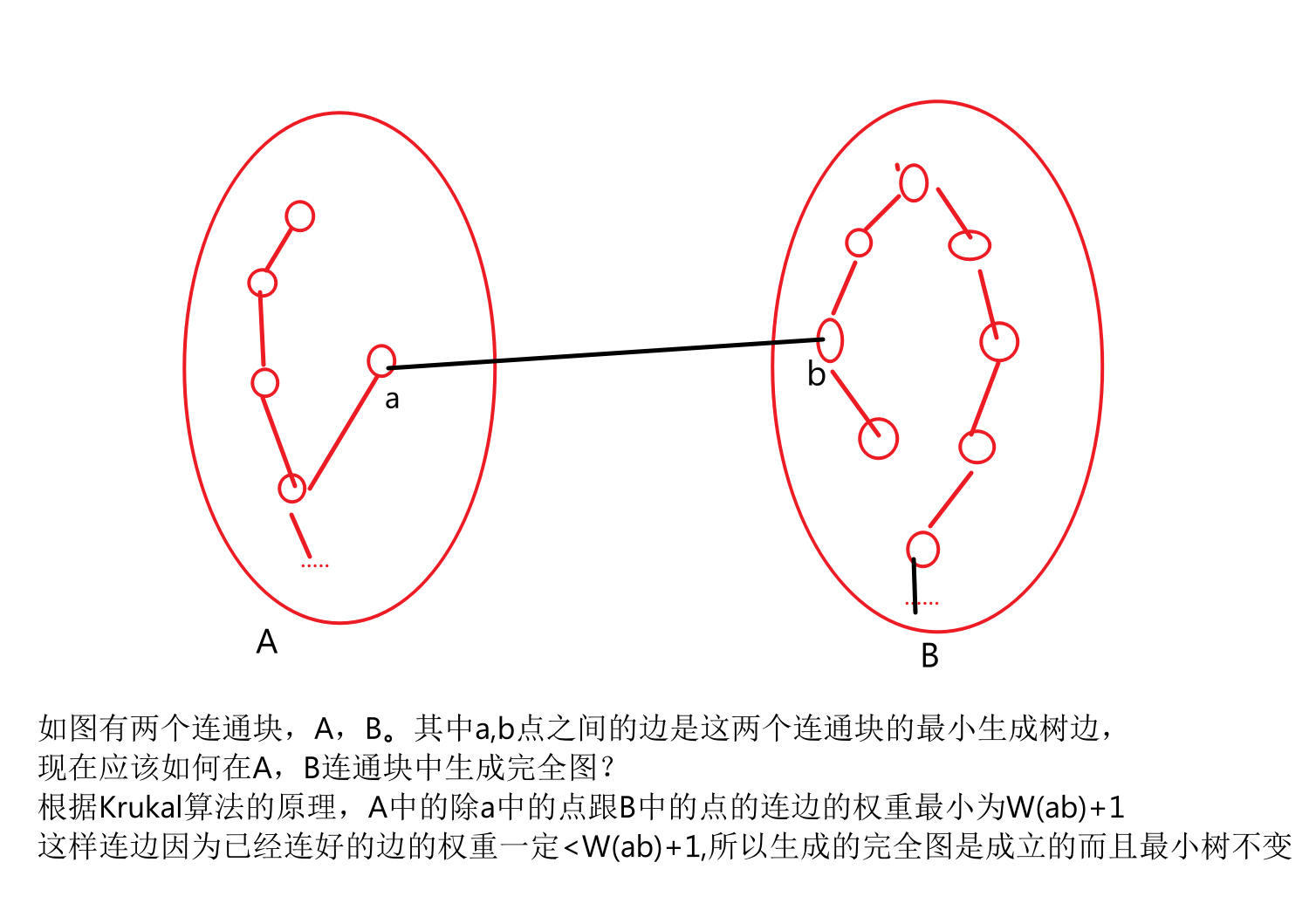
《解决最小生成树的一般思考方式》
我们一般思考最小生成树都最好将其看做连通块的合并来看,
因为一个连通块中的关系我们是不用考虑的(因为这里面的最小生成树已经生成)
然后最小生成树就成了多个连通块之间连上一条边的问题,极大地减少了复杂性

1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 using namespace std;
5 const int N = 6001;
6 int sizes[N], fa[N];
7 struct Node
8 {
9 int a, b, w;
10 } sides[N];
11 int find(int x)
12 {
13 if (fa[x] != x)
14 fa[x] = find(fa[x]);
15 return fa[x];
16 }
17 int main()
18 {
19 int t;
20 cin >> t;
21 while (t--)
22 {
23 int n;
24 cin >> n;
25 for (int i = 1; i <= n - 1; i++)
26 {
27 int a, b, w;
28 cin >> a >> b >> w;
29 sides[i] = {a, b, w};
30 }
31 sort(sides + 1, sides + n, [](struct Node a, struct Node b)
32 { return a.w < b.w; });
33 for (int i = 1; i <= n; i++)
34 {
35 fa[i] = i;
36 sizes[i] = 1;
37 }
38 int res = 0;
39 for (int i = 1; i <= n - 1; i++)
40 {
41 int u = sides[i].a, v = sides[i].b, w = sides[i].w;
42 int fu = find(u), fv = find(v);
43 if (fu != fv)
44 {
45 res += (sizes[fu] * sizes[fv] - 1) * (w + 1);
46 fa[fv] = fu;
47 sizes[fu] += sizes[fv];
48 }
49 }
50 cout << res << endl;
51 }
52 return 0;
53 }
《次小生成树》

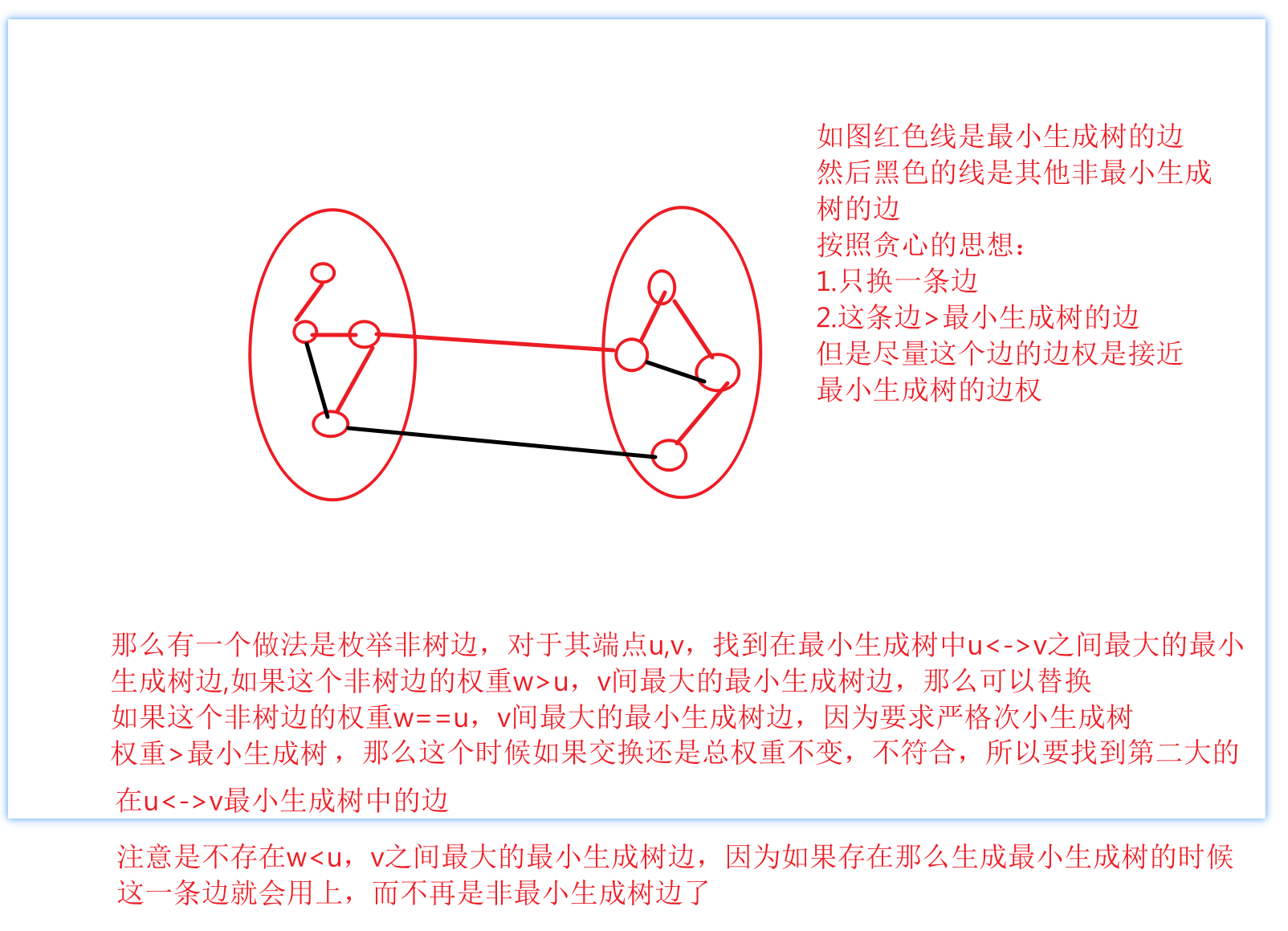
更详细博客:https://www.acwing.com/solution/content/8300/
关于如何求任意两点之间最小生成树的最大边权的dfs有点讲究
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 #include <vector>
5 using namespace std;
6 const int N = 501, M = 1e4 + 1;
7 vector<int> sides[N];
8 vector<int> sidesW[N];
9 int fa[N], n, m;
10 struct Node
11 {
12 int u, v, w;
13 bool isTree;
14 } nodes[M];
15 int find(int x)
16 {
17 if (fa[x] != x)
18 fa[x] = find(fa[x]);
19 return fa[x];
20 }
21 int dist1[N][N], dist2[N][N];
//x为当前的点,f是x的父节点,maxN是已求出的最大边权,ermaxN是已求出的第二最大边权
//d1是dist1[i][],表示i点到x点的最大边权,d2是dist2[i][]表示i点到x点的第二最大边权
22 void dfs(int x, int f, int maxN, int ermaxN, int d1[], int d2[])
23 {
24 d1[x] = maxN;
25 d2[x] = ermaxN;
26 for (int i = 0; i < sides[x].size(); i++)
27 {
28 int child = sides[x][i], w = sidesW[x][i];
29 //十分注意这里直接改变maxN与ermaxN是一个十分愚蠢的做法
30 //因为到时候我还要回溯,如果改变了而没有还原
31 //则会出现十分严重的问题
32 if (child != f)
33 {
34 int m1 = maxN, m2 = ermaxN;
35 if (w > m1)
36 {
37 m2 = m1;
38 m1 = w;
39 }
40 else if (w < m1 && w > m2)
41 m2 = w;
42 dfs(child, x, m1, m2, d1, d2);
43 }
44 }
45 }
46 long long sum = 0;
47 void Kruskal()
48 {
49 for (int i = 1; i <= n; i++)
50 fa[i] = i;
51 sort(nodes + 1, nodes + 1 + m, [](struct Node a, struct Node b)
52 { return a.w < b.w; });
53 for (int i = 1; i <= m; i++)
54 {
55 int u = nodes[i].u, v = nodes[i].v, w = nodes[i].w;
56 int fu = find(u), fv = find(v);
57 if (fu != fv)
58 {
59 fa[fv] = fu;
60 sum += w;
61 /* cout << u << " " << v << endl; */
62 sides[u].push_back(v), sides[v].push_back(u);
63 sidesW[u].push_back(w), sidesW[v].push_back(w);
64 nodes[i].isTree = true;
65 }
66 }
67 }
68 int main()
69 {
70 scanf("%d%d", &n, &m);
71 for (int i = 1; i <= m; i++)
72 {
73 int a, b, w;
74 scanf("%d%d%d", &a, &b, &w);
75 nodes[i] = {a, b, w, false};
76 }
77 //生成最小生成树
78 Kruskal();
79 //找到任意两个点之间的最大边权数
80 for (int i = 1; i <= n; i++)
81 dfs(i, -1, 0, 0, dist1[i], dist2[i]);
82 /* cout << "success" << endl; */
83 //枚举每一条非树边,找到一条非树边的>这个边在最小生成树中两个点之间的最大边权数
84 //然后取这个中最小的
85 long long res = 1e18;
86 for (int i = 1; i <= m; i++)
87 {
88 int u = nodes[i].u, v = nodes[i].v, w = nodes[i].w;
89 if (!nodes[i].isTree)
90 {
91 if (w > dist1[u][v])
92 res = min((sum - dist1[u][v] + w), res);
93 else if (w == dist1[u][v] && w > dist2[u][v])
94 res = min((sum - dist2[u][v] + w), res);
95 }
96 }
97 cout << res;
98 return 0;
99 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号