dp----状态机模型

《需求引出》

《情况一：》

在一般的dp问题中，我们的当前项都是可以由前一项推出的，

但是在一些情况下我们要用到前前项的情况,这个时候可以将这个情况当做一个状态表示出来，进行转移

 

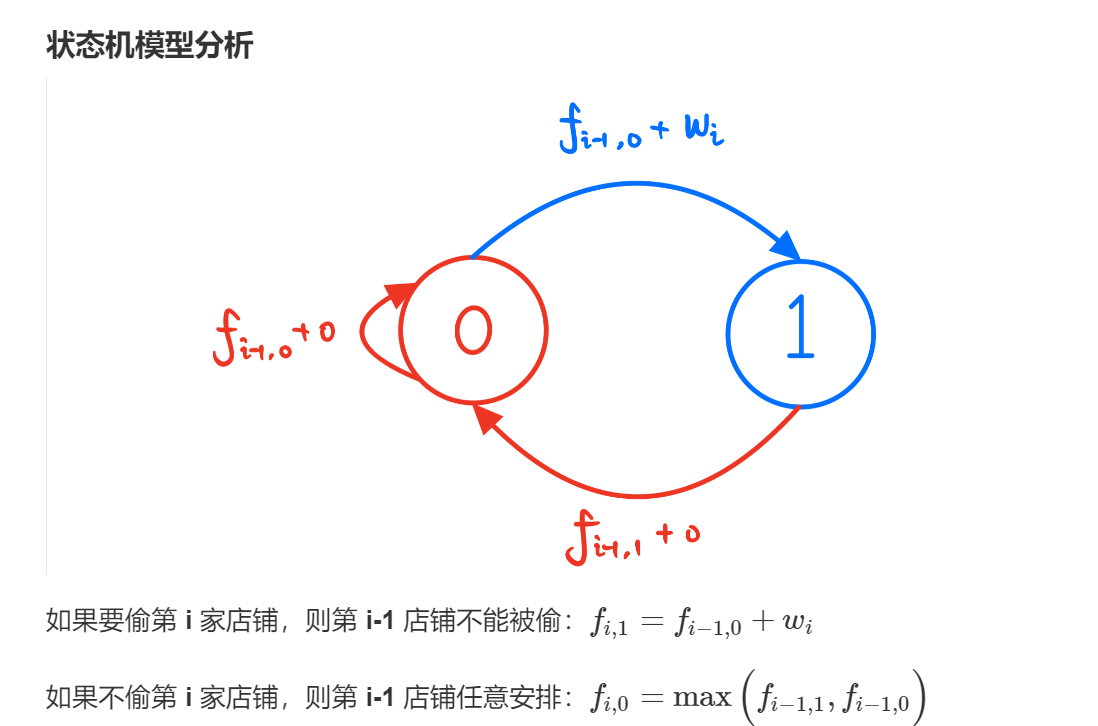
 其中0表示：f[i][0]:在第i家店铺，不偷时的最大值

其中1表示：f[i][1]：在第i家店铺，偷时的最大值

转载博客：https://www.acwing.com/problem/content/1051/

《情况二：》

当状态在一个dp表达式中信息太多，无法知晓转移，可以进行状态的拆分

 

 

 

 

 

 

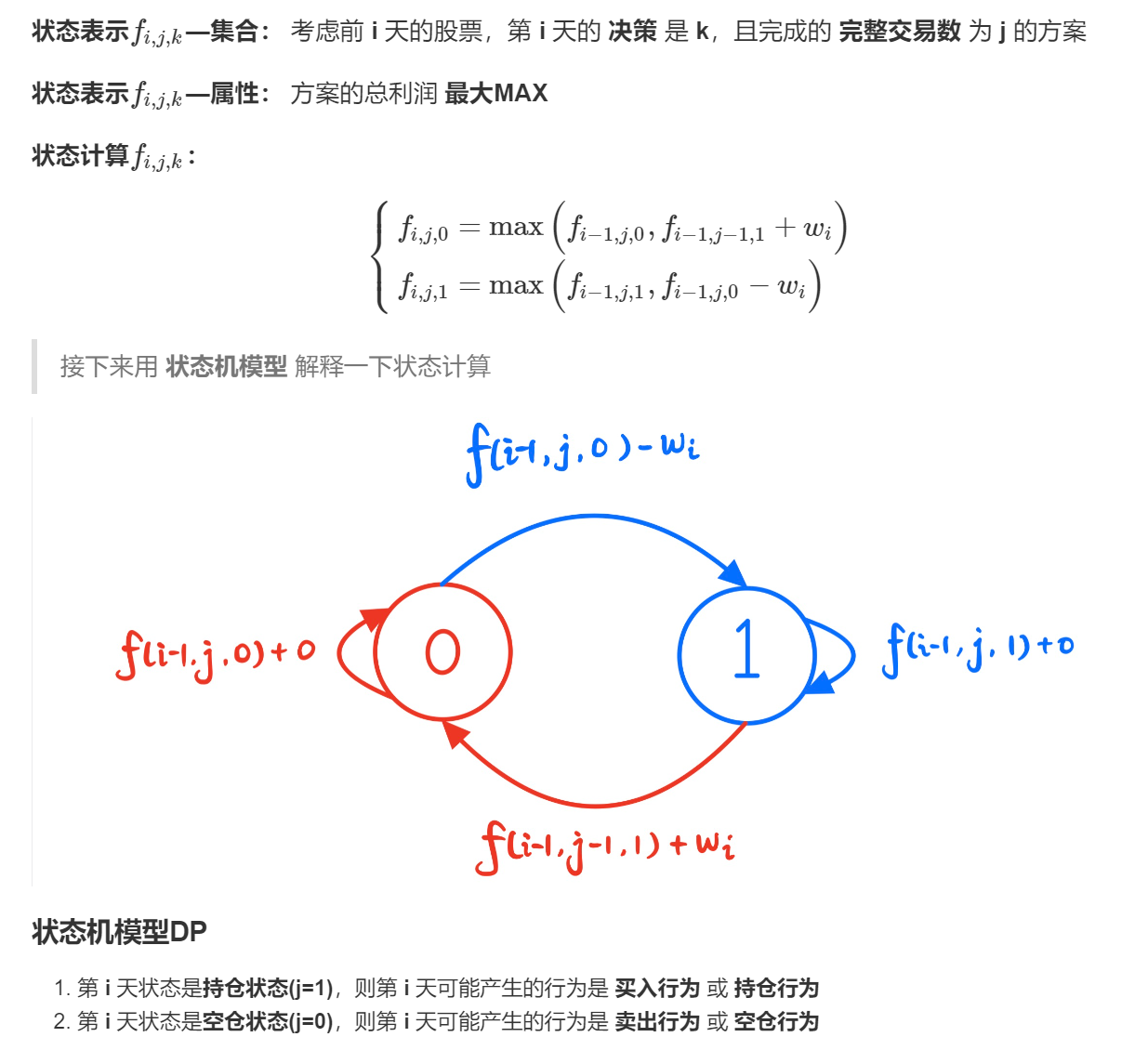
 转载博客：https://www.acwing.com/solution/content/55147/

 《KMP状态机》

参考博客：https://www.acwing.com/solution/content/28022/

https://www.acwing.com/solution/content/55449/

 

 

 

 

 

 

 

 

 《题目》

 

 

 前置知识:https://oi-wiki.org/string/kmp/

https://oi-wiki.org/string/automaton/

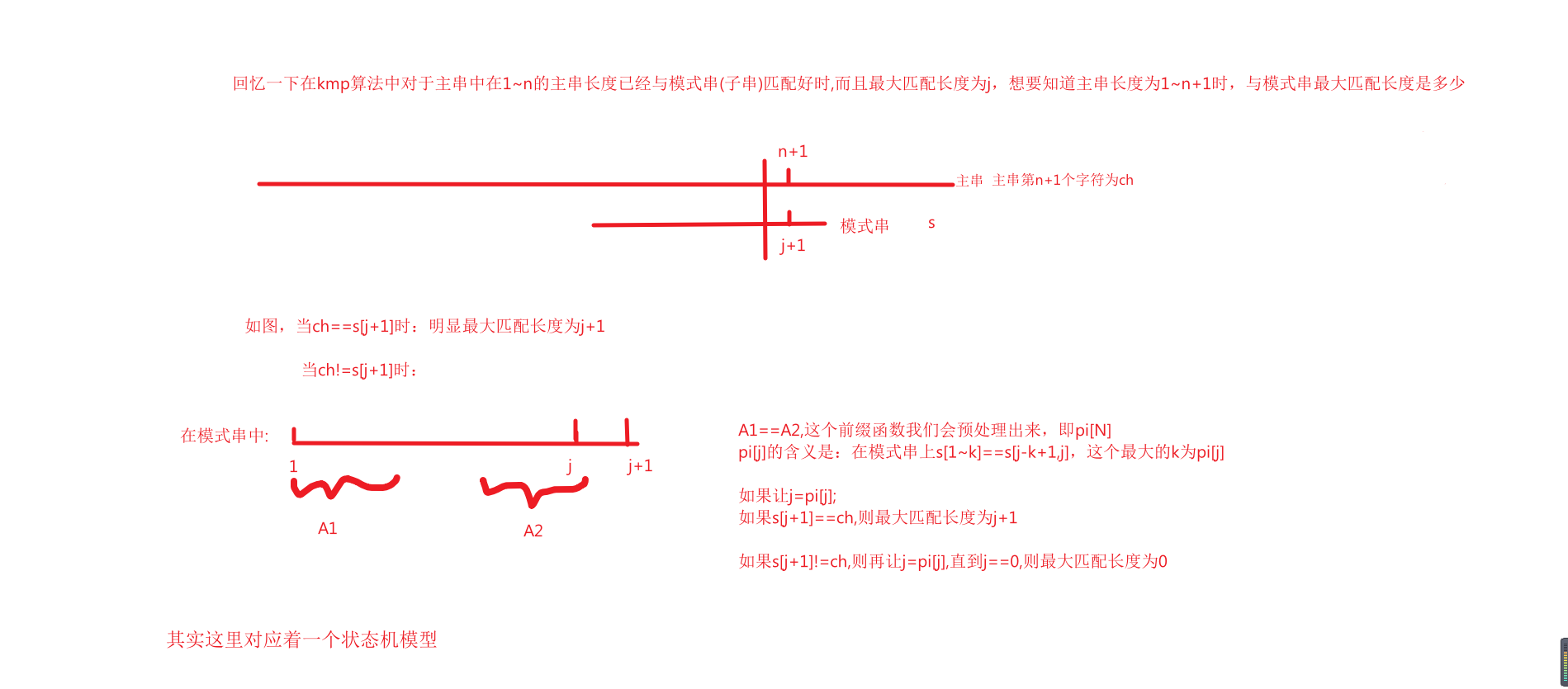
对于一个主串，只要我们可以让模式串在与主串匹配时，让模式串匹配出的最大匹配长度j<模式串长度len即可

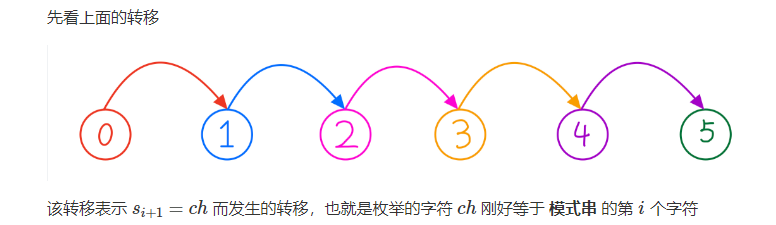
想象一下我们在匹配主串时，如主串长度1~n匹配好时，在去通过上一个匹配的信息来匹配主串1~n+1的长度，而正好是那第n+1个字符决定j在模式串的变动

我们可以去枚举主串上第n+1个字符

$(j,ch):表示当在枚举主串的长度为n+1时的字符为ch,而且在主串的长度为n时，模式串与主串的最大匹配长度是j时的最大匹配长度

$(j,ch)=j+1,　　s[j+1]==ch

$(j,ch)=$(pi[j],ch),　　s[j+1]!=ch && s[pi[j]]==ch && j>0

$(j,ch)=0 ,　　s[j+1]!=ch && j<=0;

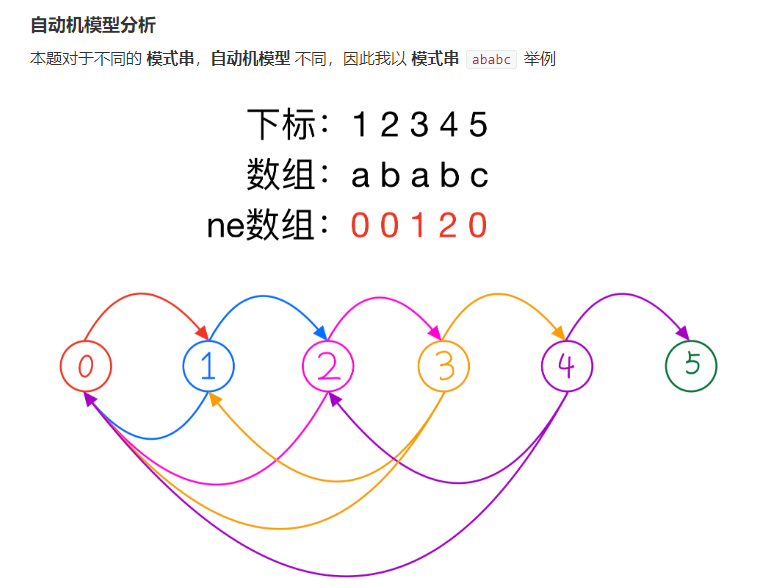
当$(j,ch)!=模式串的长度，说明我们枚举的主串第n+1个字符ch是成立的

《dp计数》

dp[i][j]:表示在主串枚举第i+1个字符时，而且在枚举上一个字符时的最大匹配长度为j时的主串字符个数

 

 

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 55, mod = 1e9 + 7;
char s[N];
int pi[N];
int n, dp[N][N];
// dp[i][j]表示在主串长度为i时，模式串s与主串最大的匹配长度为j时一共有dp[i][j]个主串可以达成这样
//因为在看一个主串中是否有模式串s，根据kmp算法可得:是看模式串在匹配时的与主串最大匹配长度是否为模式串的长度
//在这里只要是dp[n][j],j<len（模式串的长度），都是正确答案
// dp[i+1][k]可以通过前面的dp[i][kk]来推导；
int main()
{
    cin >> n >> (s + 1);
    int len = strlen(s + 1);
    pi[1] = 0;
    //用kmp处理child的前缀函数:child[1~k]==child[i-k+1,i]的max(k);
    int j = 0;
    for (int i = 2; i <= len; i++)
    {
        while (j && s[i] != s[j + 1])
            j = pi[j];
        if (s[i] == s[j + 1])
            j++;
        pi[i] = j;
    }
    dp[0][0] = 1;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < len; j++)
            //枚举主串上第i+1个字符，假设第i个字符已经匹配完成，而且最大长度为j
            for (int ch = 'a'; ch <= 'z'; ch++)
            {
                int pre = j;
                while (pre && s[pre + 1] != ch)
                    pre = pi[pre];
                if (ch == s[pre + 1])
                    pre++;
                dp[i + 1][pre] = (dp[i + 1][pre] + dp[i][j]) % mod;
            }
    int res = 0;
    for (int i = 0; i < len; i++)
        res = (res + dp[n][i]) % mod;
    cout << res;
    return 0;
}