数论----同余方程
《贝祖定理》
简单来说是: 整数 a,b ,gcd(a,b)=d; 则 存在x,y使ax+by=d成立
证明:
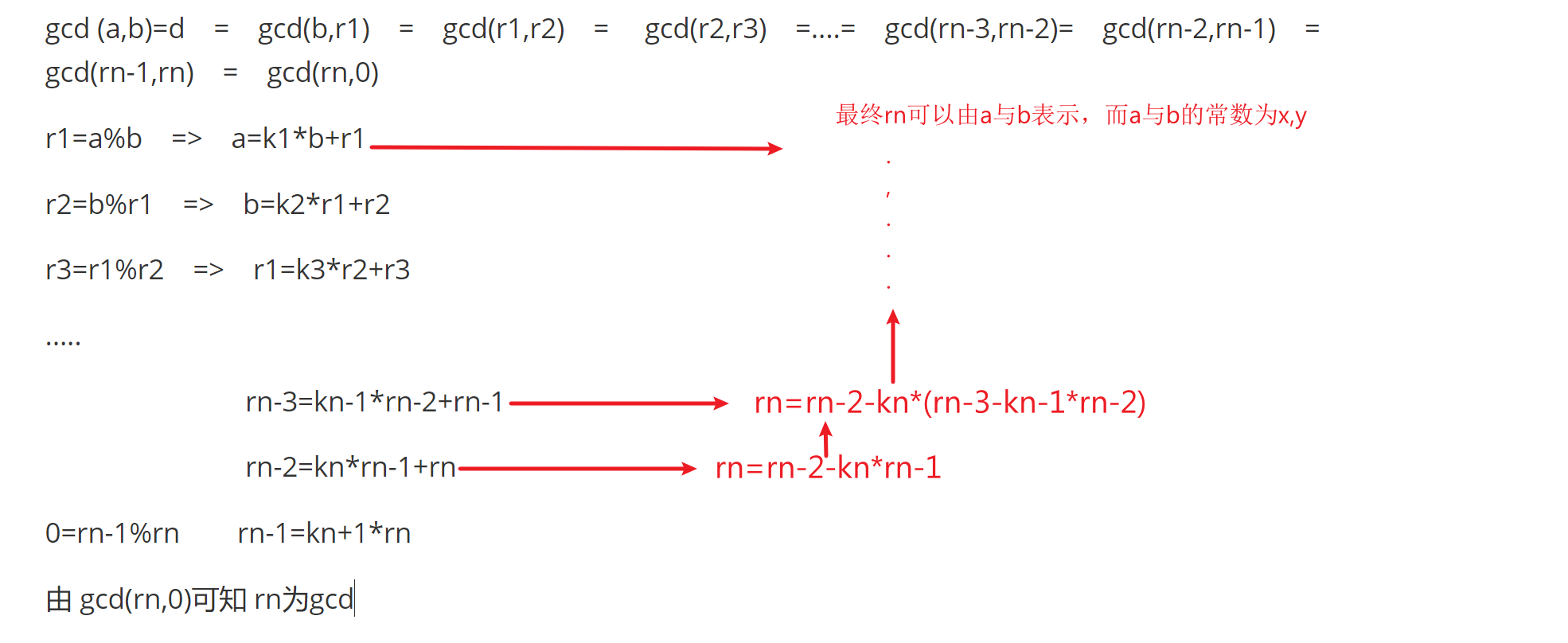
《扩展欧几里得算法》
好博客:https://blog.csdn.net/syz201558503103/article/details/76512144
https://blog.csdn.net/qq_44765711/article/details/102688064
由贝祖定理:ax+by=gcd(a,b)
则:当不断取模gcd(a,b)=......=gcd(an,0)时
an*x+b*0=gcd,而an=gcd,所以 x=1,y=任意,为了方便y=0;
设:当前层ax+by=gcd
已知下一层的x1,y1
由下一层->这一层:
下一层的 a1=b,b1=a%b
a%b=a-(a/b)*b
即 b*x1+(a-(a/b)*b)*y1=gcd
a*y1+ b*(x1-y1*(a/b))=gcd------>x=y1,y=x1-y1*(a/b)
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 using namespace std;
5 int exgcd(int a, int b, int &x, int &y)
6 {
7 if (!b)
8 {
9 x = 1, y = 0;
10 return a;
11 }
12 //这里不用担心a<b的情况,因为在下一层通过b,b%a交换了一下
13 int d = exgcd(b, a % b, x, y);
14 int t = x;
15 x = y;
16 y = t - (a / b) * y;
17 return d;
18 }
19 int main()
20 {
21 int t;
22 cin >> t;
23 while (t--)
24 {
25 int a, b, x, y;
26 scanf("%d%d", &a, &b);
27 exgcd(a, b, x, y);
28 printf("%d %d\n", x, y);
29 }
30 return 0;
31 }
《通解》

《ax+by=k && gcd(a,b)|k的求解方法》
对于 ax+by=gcd(a,b)的一组特解:(x0,y1)
在这里我要重点说明一下:扩展欧几里得算法是求ax+by=gcd(a,b)的算法
而不是求ax+by=k的算法
ax+by=k && gcd(a,b)|k的一组特解为
(x0*w,y0*w),其中w=k/gcd(a,b);
证明:
代入即可:
a*x0*k/gcd(a,b)+b*y0*k/gcd(a,b)=k--------------->
a*x0+b*y0=gcd(a,b)是成立的
《对于ax+by=k的通解》
我们令 x1=x0*w,y1=y0*w;


《求ax+by=k的解的个数》

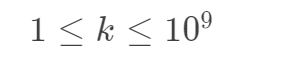
由:
f(2)=x+y
f(3)=x+2y
f(4)=2x+3y
f(5)=3x+5y
f(6)=5x+8y
....
可以得到x与y前系数的规律:即其实个斐波那契数列:
有g(0)=1,g(1)=1
f(i)=g(i-2)*x+g(i-1)*y
我们可以预处理g(),这个斐波那契数列在g(45)时已经>1e9,而明显对于ax+by=k的求解
在x && y>0的情况下 a && b<1e9
我们可以枚举0~45的g()
然后问题变成了求g(i-1)*x+g(i)*y=k的x和y的解的个数问题
然后根据一顿操作(我上面讲了)求通解:
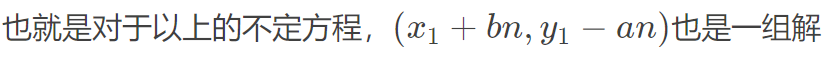
这里b=g(i),a=g(i-1)

基本思路是:
当求出的x1<=0时,让其变为最小的>0的整数解,根据通解的形式可以判断出这个时候y1是最大的y1了
然后看一下这个时候的y1最大能够减多少个a
通过y1/a,假设y1/a=n
则有解:y1,y1-a,y1-a*2......,y1-a*n
当y1%a==0时,y1-a*n是不行的,因为解要>0,
则:当y1%a==0时,解有y1/a个解,否则有y1/a+1个解
当求出y1<=0时同理
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 using namespace std;
5 typedef long long ll;
6 const ll mod = 1e9 + 7;
7 int k;
8 ll f[50];
9 ll exgcd(ll a, ll b, ll &x, ll &y)
10 {
11 if (!b)
12 {
13 x = 1, y = 0;
14 return a;
15 }
16 ll gcd = exgcd(b, a % b, x, y);
17 ll t = x;
18 x = y;
19 y = t - (a / b) * y;
20 return gcd;
21 }
22 int main()
23 {
24 scanf("%d", &k);
25 f[0] = 1, f[1] = 1;
26 for (int i = 2; i <= 45; i++)
27 f[i] = f[i - 1] + f[i - 2];
28 /* 当f[44]时就已经超过1e9了
29 cout<<f[44]; */
30 //对于每一个f[i-1]x+f[i]y=k,都要看一下
31 ll ans = 0;
32 for (int i = 1; f[i] < k; i++)
33 {
34 //首先求出f[i-1]x+f[i]y=gcd(f[i-1],f[i])=1的特解x0,y0
35 ll x0, y0;
36 ll gcd = exgcd(f[i - 1], f[i], x0, y0);
37 //然后求出f[i-1]x+f[i]y=k的特解
38 //其特解为x0*k/gcd,y0*k/gcd,这里为x0*k,y0*k
39 x0 *= k, y0 *= k;
40 //因为要求x>0,y>0,如果开始求出的x0 || y0<=0,我们就要将其变为>0
41 ll t = 0;
42 if (x0 <= 0)
43 {
44 //这个操作后,x0一定会>0
45 t = -x0 / f[i] + 1;
46 x0 += f[i] * t;
47 y0 -= f[i - 1] * t;
48 //如果让x0成为最小>0后,y0<=0说明无解
49 if (y0 <= 0)
50 continue;
51 ans += (y0 % f[i - 1] == 0) ? y0 / f[i - 1] : y0 / f[i - 1] + 1;
52 ans %= mod;
53 }
54 else if (y0 <= 0)
55 {
56 //让y0变成最小整数解
57 //则 变后: ymin=y0+(y0/f[i-1]+1)*f[i-1],xmax=x0-f[i]*(y0/f[i-1]+1);
58 t = -y0 / f[i - 1] + 1;
59 y0 += f[i - 1] * t;
60 x0 -= f[i] * t;
61 if (x0 <= 0)
62 continue;
63 ans += (x0 % f[i] == 0) ? x0 / f[i] : x0 / f[i] + 1;
64 ans %= mod;
65 }
66 }
67 printf("%lld", ans);
68 return 0;
69 }
《一元线性同余方程》


由 ax mod b =c ---> ax=y*b+c-----> ax+by=c
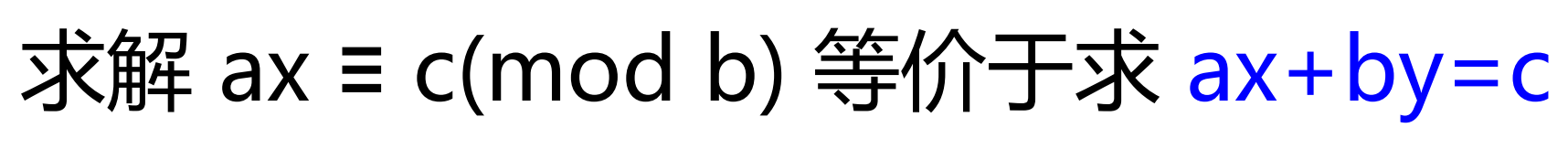

《中国剩余定理》


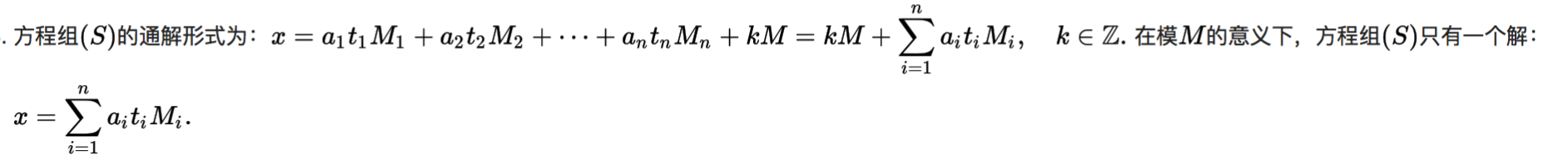
《证明》
1.首先通解形式肯定是原方程组的解(一个一个代进去会发现都成立)
2.

这里说明一下为啥 x1-x2≡0(modmi)
因为
则 x1=k1*mi+ai , x2 =k2* mi+ai
x1-x2=(k1-k2)*mi---->x1-x2≡0(modmi)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号