异或运算

《运算性质》

 

 注意其并没有这个性质：(a+b)^c=a^c+b^c,简单举个例子就可以推出这个性质不成立

注意是有这个性质的：a*b^a*c=a*(b^c)

 

 

 即：

a11*n1^a12*n2^a13^n3.............a1n^nn=b1

a21*n1^a22*n2^a23^n3.............a2n^nn=b2

则：

n1*(a11^a21)^n2*(a12^a22)^.........^nn*(a1n^a2n)=b1^b2

 

《问题的解决之道----前缀和》

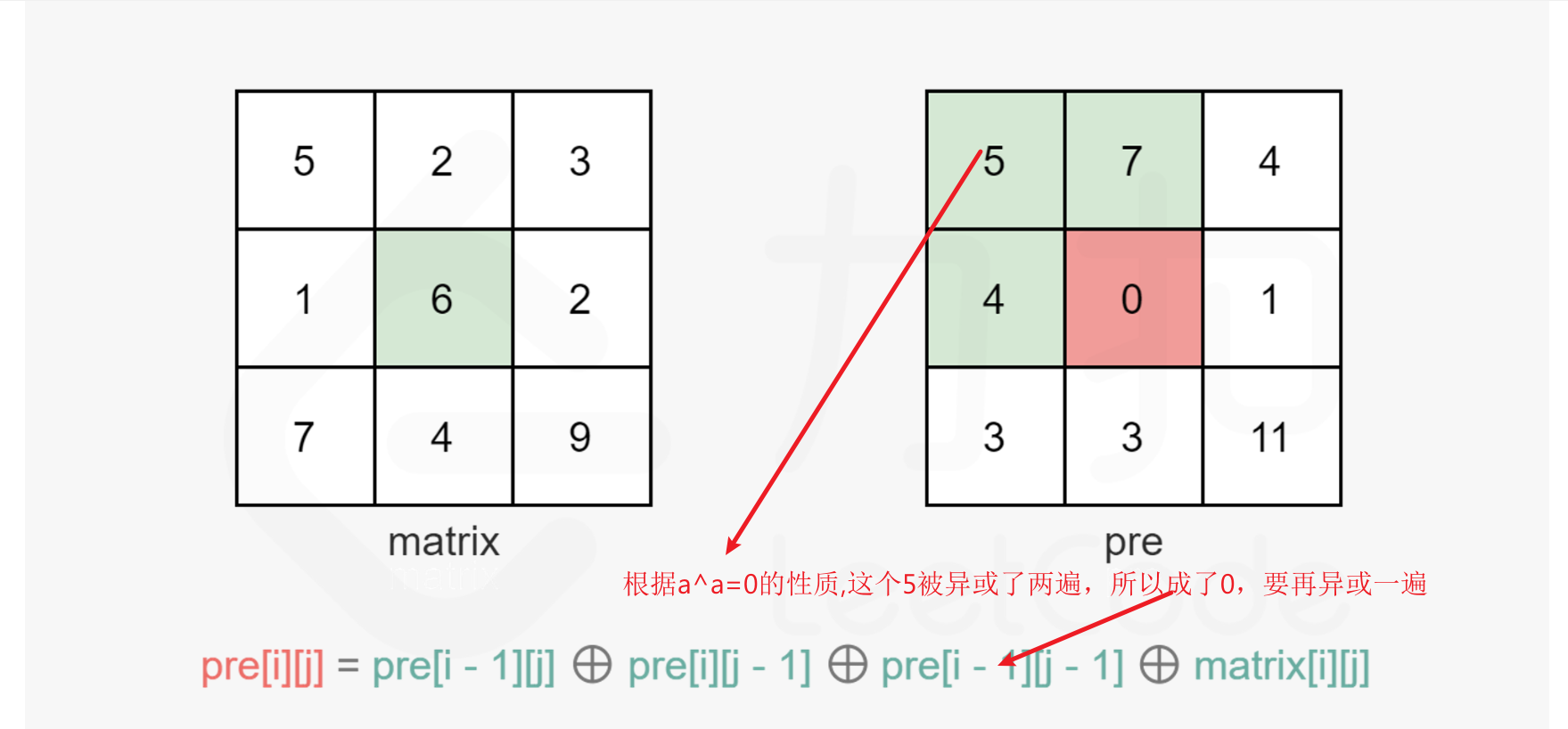
 《问题解决之道----拆位（转化为二进制下的形式）》

原题：https://www.luogu.com.cn/problem/solution/CF242E

 

 基本思想是：开一个线段树，struct tree{}中除了 int l,r,lazy之外，还有用个cnt[]数组，cnt[i]用来记录区间[l,r]中全部数在

转化为二进制的情况下在第i位上1的个数

然后当要在区间[l,r]上修改时，即^x ，将x拆成二进制，根据^的性质，如果第i位为1，cnt[i]中的全部1变为0,0变为1

如果是0则不用变化

到最后只要将二进制转化为十进制即可

  1 #include <iostream>
  2 #include <algorithm>
  3 #include <cstring>
  4 using namespace std;
  5 const int N = 100010, K = 20;
  6 #define sl (u << 1)
  7 #define sr (u << 1 | 1)
  8 typedef long long LL;
  9 int w[N];
 10 struct tree
 11 {
 12     // cnt[i]记录的是这个区间上,二进制下第i位一共有cnt[i]个1
 13     //最后算总和时:sum+=(1<<i)*cnt[i];
 14     // lazy懒标记,积累的^是多少
 15     int l, r, cnt[K], lazy;
 16 } tr[N * 4];
 17 LL sum(int cnt[])
 18 {
 19     LL res = 0, t = 1;
 20     for (int i = 0; i < 20; i++)
 21         res += (1LL << i) * cnt[i];
 22     return res;
 23 }
 24 //用子节点更新父节点u的操作
 25 void pushup(int u)
 26 {
 27     for (int i = 0; i < 20; i++)
 28         tr[u].cnt[i] = tr[sl].cnt[i] + tr[sr].cnt[i];
 29 }
 30 //将父节点u的lazy标记下放的操作
 31 void pushdown(int u)
 32 {
 33     if (tr[u].lazy)
 34     {
 35         for (int i = 0; i < 20; i++)
 36         {
 37             // lazy二进制化
 38             //如果lazy这一位是1则要改变
 39             if ((tr[u].lazy >> i) & 1)
 40             {
 41                 tr[sl].cnt[i] = (tr[sl].r - tr[sl].l + 1) - tr[sl].cnt[i];
 42                 tr[sr].cnt[i] = (tr[sr].r - tr[sr].l + 1) - tr[sr].cnt[i];
 43             }
 44         }
 45         tr[sl].lazy ^= tr[u].lazy;
 46         tr[sr].lazy ^= tr[u].lazy;
 47         tr[u].lazy = 0;
 48     }
 49 }
 50 void build(int u, int l, int r)
 51 {
 52     tr[u].l = l, tr[u].r = r, tr[u].lazy = 0;
 53     if (l == r)
 54     {
 55         for (int i = 0; i < 20; i++)
 56         {
 57             tr[u].cnt[i] = (w[l] >> i) & 1;
 58         }
 59         return;
 60     }
 61     int mid = l + r >> 1;
 62     build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
 63     pushup(u);
 64 }
 65 //区间修改
 66 void modify(int u, int l, int r, int d)
 67 {
 68     if (tr[u].l >= l && tr[u].r <= r)
 69     {
 70         for (int i = 0; i < 20; i++)
 71             if ((d >> i) & 1)
 72                 tr[u].cnt[i] = (tr[u].r - tr[u].l + 1) - tr[u].cnt[i];
 73         tr[u].lazy ^= d;
 74         return;
 75     }
 76     pushdown(u);
 77     int mid = tr[u].l + tr[u].r >> 1;
 78     if (l <= mid)
 79         modify(sl, l, r, d);
 80     if (r > mid)
 81         modify(sr, l, r, d);
 82     //上面u的子节点发生的变化，要pushup
 83     pushup(u);
 84 }
 85 //区间询问
 86 LL query(int u, int l, int r)
 87 {
 88     if (tr[u].l >= l && tr[u].r <= r)
 89         return sum(tr[u].cnt);
 90     pushdown(u);
 91     int mid = tr[u].l + tr[u].r >> 1;
 92     LL res = 0;
 93     if (l <= mid)
 94         res += query(u << 1, l, r);
 95     if (r > mid)
 96         res += query(u << 1 | 1, l, r);
 97     return res;
 98 }
 99 int main()
100 {
101     int n;
102     cin >> n;
103     for (int i = 1; i <= n; i++)
104         scanf("%d", &w[i]);
105     build(1, 1, n);
106     int m;
107     cin >> m;
108     while (m--)
109     {
110         int op;
111         int l, r, d;
112         scanf("%d%d%d", &op, &l, &r);
113         if (op == 1)
114         {
115             printf("%lld\n", query(1, l, r));
116         }
117         else
118         {
119             int x;
120             cin >> x;
121             modify(1, l, r, x);
122         }
123     }
124     return 0;
125 }

 《题目训练中有xor问题的》

1.https://www.cnblogs.com/cilinmengye/p/17011231.html

posted @ 2022-08-18 22:26  次林梦叶  阅读(57)  评论(0)    收藏  举报