线段树----区间问题的神

《标准线段树》

 

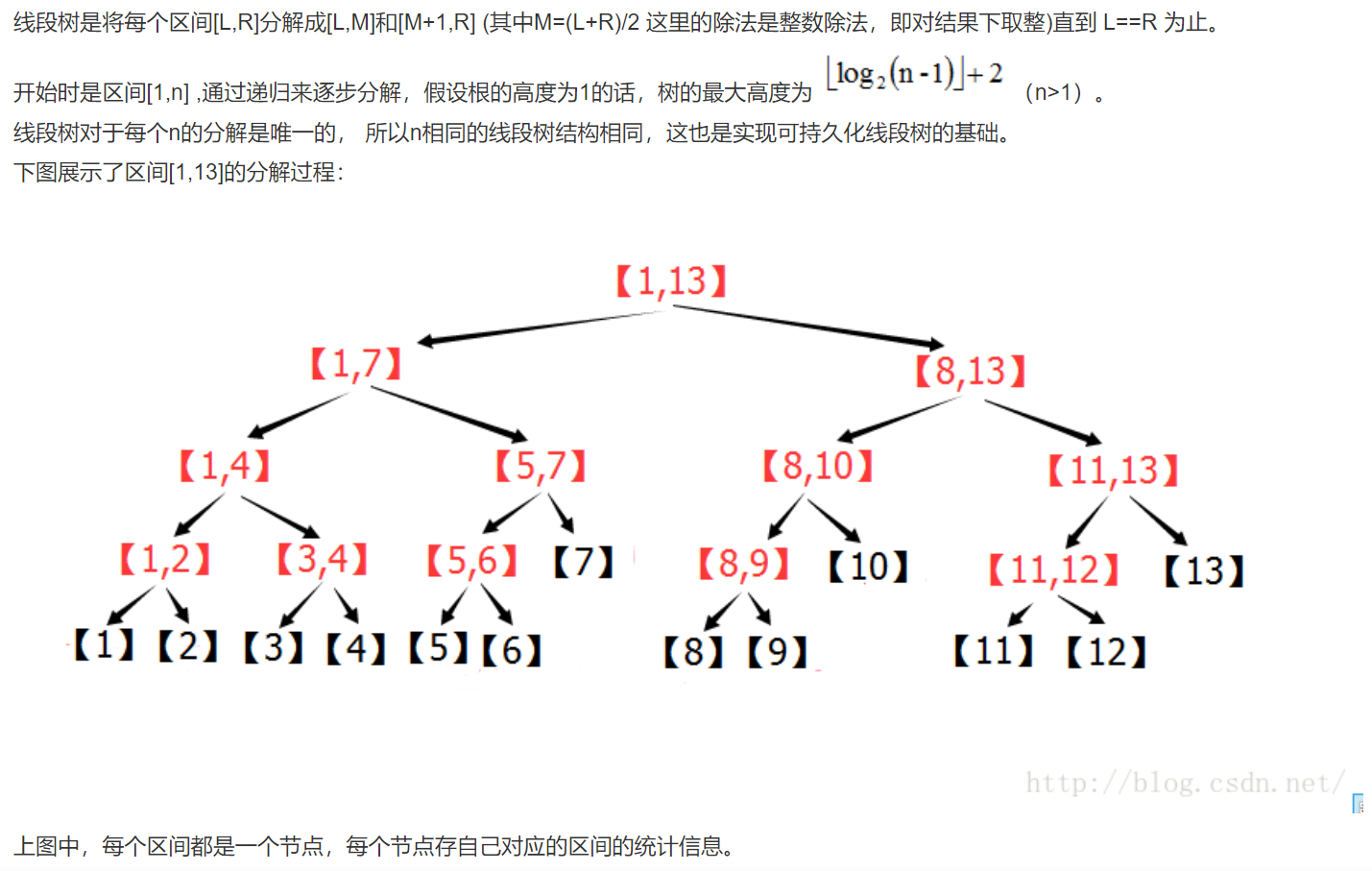
 普通的线段树，其区间一般都是一个序列的数的个数，但还是要根据不同题目来判断

注意：tr[]空间是N*4，N为最大范围

《单点修改，区间查询》

原题：https://www.acwing.com/problem/content/1277/

 

 

 

 

 像这道题，N最大为2*1e5,我们可以事先建立一颗最大范围1~N的线段树，然后不断分裂这个范围，产生子节点，

每一个节点维护的信息是，这个节点代表的区间的最大值，这里范围代表数的个数；

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 200010;
struct tree
{
    int l, r;
    //区间[l,r]中的最大值
    int v;
} tr[N * 4];
//由子节点维护的信息计算（或更新）父节点维护的信息
void pushup(int u)
{
    //解释一下 u<<1|1这个操作:
    //对于2的倍数,其二进制下的第一位总是0,根据这个特性|1,相当于+1;
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}
//将tr[u]这个位置初始化为树
void build(int u, int l, int r)
{
    tr[u].l = l, tr[u].r = r;
    if (l == r)
        return;
    //维护信息根据题目的不同,在代码中的写法也不同
    //这里因为是以逐渐加点(在modify中)来产生信息,
    //在最开始的建树过程是无维护信息的,所以这里不管tr[u].v;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
//单点修改,将tr[u]包含区间中的位置为x的值修改为v;
void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x)
        tr[u].v = v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid)
            modify(u << 1, x, v);
        else
            modify(u << 1 | 1, x, v);
        //注意这个pushup()操作一定要写到这里,而不是写到外面
        // pushup操作是更新父节点u的维护信息，其是写在子节点u<<1,u<<1|1被更新时写的
        //如果写在外面,当 if (tr[u].l == x && tr[u].r == x)tr[u].v = v; 生效时
        //这个时候u是无子节点的,那就会问:这个u点更新了,那如何更新其父节点呢?
        //很简单,因为在modify时,我们会传入的u是1，即根节点，此后都是递归去更新
        pushup(u);
    }
}
//查询在点u包含的范围内中[l,r]的维护的信息
int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
        return tr[u].v;
    //注意这里v是取题中数的最小值
    int v = 0;
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid)
        v = query(u << 1, l, r);
    //注意:这里就不是else了
    if (r > mid)
        v = max(v, query(u << 1 | 1, l, r));
    return v;
}
int main()
{
    int m, p, a = 0, x, n = 0;
    cin >> m >> p;
    char op[2];
    build(1, 1, m);
    while (m--)
    {
        scanf("%s%d", op, &x);
        if (op[0] == 'A')
        {
            //注意这里可能爆int;
            modify(1, n + 1, ((LL)a + x) % p);
            n++;
        }
        else
        {
            a = query(1, n - x + 1, n);
            printf("%d\n", a);
        }
    }
    return 0;
}

《时间复杂度》

《区间修改，区间查询》

对于区间修改，tree结构体中要多一个变量lazy,用来记录整个区间的修改，是缓存下放到修改子区间的值

注意：不是缓存修改本区间，本区间的维护的信息是要随时修改的

lazy标记的作用：

 

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
typedef long long LL;
int w[N];
struct tree
{
    // sum是区间[l,r]要维护的信息
    // lazy是在多次修改时，将修改的数先累加起来,即先不下放修改给子区间
    //到这个区间的lazy不平衡时才下放(如[1,10],先整个区间+10,再[5,10]区间+5,这个时候区间lazy不能平衡，要下放)
    //当前的sum是可以即时修改的
    int l, r, lazy;
    LL sum;
} tr[N * 4];
//用子节点更新父节点u的操作
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
//将父节点u的lazy标记下放的操作
void pushdown(int u)
{
    //如果积累下来的lazy有修改:
    if (tr[u].lazy)
    {
        int sl = u << 1, sr = u << 1 | 1;
        //注意lazy这里是+=
        tr[sl].lazy += tr[u].lazy;
        //注意可能会爆int
        tr[sl].sum += (LL)(tr[sl].r - tr[sl].l + 1) * tr[u].lazy;

        tr[sr].lazy += tr[u].lazy;
        tr[sr].sum += (LL)(tr[sr].r - tr[sr].l + 1) * tr[u].lazy;
        //全部下放成功,清空:
        tr[u].lazy = 0;
    }
}
void build(int u, int l, int r)
{
    tr[u].l = l, tr[u].r = r;

    if (l == r)
    {
        tr[u].lazy = 0;
        tr[u].sum = w[l];
        return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    //子节点变化,pushup
    pushup(u);
}
//区间修改
void modify(int u, int l, int r, int d)
{
    //注意这里与单点修改有着极不一样的地方
    if (tr[u].l >= l && tr[u].r <= r)
    {
        //注意这里tr[u].sum是+=
        tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * d;
        tr[u].lazy += d;
        return;
    }
    // u管辖的区间太大,接下来区间分裂,直到出现上面的情况
    //区间分裂说明,在u管辖的区间只会有一部分区间加上修改,lazy不平衡，要pushdown();
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid)
        modify(u << 1, l, r, d);
    if (r > mid)
        modify(u << 1 | 1, l, r, d);
    //上面u的子节点发生的变化，要pushup
    pushup(u);
}
//区间询问
LL query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
        return tr[u].sum;
    //当要分裂询问时
    //当然要懒标记下放,要不然父节点一直拿到修改值而不去修改也没用
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    LL res = 0;
    if (l <= mid)
        res += query(u << 1, l, r);
    if (r > mid)
        res += query(u << 1 | 1, l, r);
    return res;
}
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        scanf("%d", &w[i]);
    build(1, 1, n);
    while (m--)
    {
        char op[2];
        int l, r, d;
        scanf("%s%d%d", op, &l, &r);
        if (op[0] == 'Q')
            printf("%lld\n", query(1, l, r));
        else
        {
            scanf("%d", &d);
            modify(1, l, r, d);
        }
    }
    return 0;
}
//关于为啥modify哪里要pushdown,再pushup的原因
/* 由于modify直接修改了一些区间上面的add与sum，导致递归路径上的父节点全部都需要重新算一遍sum，所以递归结尾需要加一个pushup，

同时递归路径上如果存在带有懒标记的区间，则区间结尾的pushup会用两个子区间的返回值直接覆盖该区间的sum,但是该区间的懒标记add值还没有加到子区间上面去，也就是说懒标记的附加值就会被直接覆盖掉。
这种pushup会直接消灭懒标记，所以modify递归路径上必须全部消灭懒标记，即每一层递归都要先pushdown。

这里可以看到pushup和pushdown是一个组合，递归中每一层pushup保证了递归树的叶节点的改变对父节点的影响能够及时修正，每一层的pushdown都能保证本次的递归路径上一定不存在懒标记，保证本次递归路径上的sum赋值全部为正确值。

所以尽管查询操作并没有新增懒标记且保证递归路径上没有懒标记导致我们不需要pushup，但当我们在query的时候在每一层返回sum之前加一次pushup上述的一套组合依然能保证查询结果一定是正确的，

所以可以从这一套组合的性质出发直接 背下来，在简单运用线段树模板时候直接modify和query都用这一套，就省事很多了。
 */
//lazy不是对本区间的维护信息延迟,而是对本区间的子区间延迟
//本区间维护的信息是要时刻保持最新

《时间复杂度》

《小总结》

 

 区间询问这里是真的要根据题目的不同而变化的，要考虑如何才能正确的维护信息

《权值线段树和动态开点》

权值线段树的区间一般表示的是值域的范围，当值域过大时，如值域为【1,1e9】我们根本不可能开这么大的tr[]数组保存这些节点

（光叶节点最多也有1e9个），所以我们需要动态开点（或者可以用离散化）：

好博客：https://blog.csdn.net/qq_41673789/article/details/102773885

《可持久化线段树----主席树》

好博客：https://modestcoder.blog.csdn.net/article/details/90107874

 

 

 对于值域|A[I]|<=1e9，是我们的区间范围，但是这里，区间范围太大了，但是序列的个数却很少，

所以我们可以进行离散化，

即将一系列数，其中数的个数很小，但是数的范围很大，达到我们不可以用数组来操作

比如：我要求一个数值序列中某个数出现的次数，如果数的范围很小，我们可以用数组cnt[]来记录，每出现一个数i，就cnt[i]++;

但是如果数的范围很大如：1e9，这个时候我们可以离散化，将原本的数值映射到另一个数值上，让这个新数值来表示原来数值

如这道题：

 

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
struct Node
{
    int pos, num;
} a[N];
int cnt = 1;
//前缀和
int pre[N];
//找到不小于x的下标
int findl(int x)
{
    int l = 1, r = cnt;
    int res;
    while (l <= r)
    {
        int mid = l + r >> 1;
        if (a[mid].pos >= x)
        {
            r = mid - 1;
            res = mid;
        }
        else
            l = mid + 1;
    }
    return res;
}
//找到不大于x的下标
int findr(int x)
{
    int l = 1, r = cnt;
    int res;
    while (l <= r)
    {
        int mid = l + r >> 1;
        if (a[mid].pos <= x)
        {
            l = mid + 1;
            res = mid;
        }
        else
            r = mid - 1;
    }
    return res;
}
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        int x, c;
        cin >> x >> c;
        a[cnt++] = {x, c};
    }
    //排序
    sort(a + 1, a + cnt, [](struct Node a, struct Node b)
         { return a.pos < b.pos; });
    //去重,合并,下标i为去重后的下标
    int i, j;
    for (i = 1, j = 2; j < cnt; j++)
    {
        if (a[i].pos == a[j].pos)
            a[i].num += a[j].num;
        else
        {
            i++;
            a[i] = a[j];
        }
    }
    cnt = i;
    /*for (int i = 1; i <= cnt; i++)
    {
        cout << "!!!" << a[i].pos << " " << a[i].num << endl;
    }*/
    //求前缀和
    for (int i = 1; i <= cnt; i++)
        pre[i] = pre[i - 1] + a[i].num;
    /*for (int i = 1; i <= cnt; i++)
    {
        cout << pre[i] << " ";
    }
    cout << endl;*/
    while (m--)
    {
        int l, r;
        cin >> l >> r;
        if (l > a[cnt].pos || r < a[1].pos)
            cout << 0 << endl;
        else
        {
            int resl = findl(l), resr = findr(r);
            cout << pre[resr] - pre[resl - 1] << endl;
        }
    }
    return 0;
}

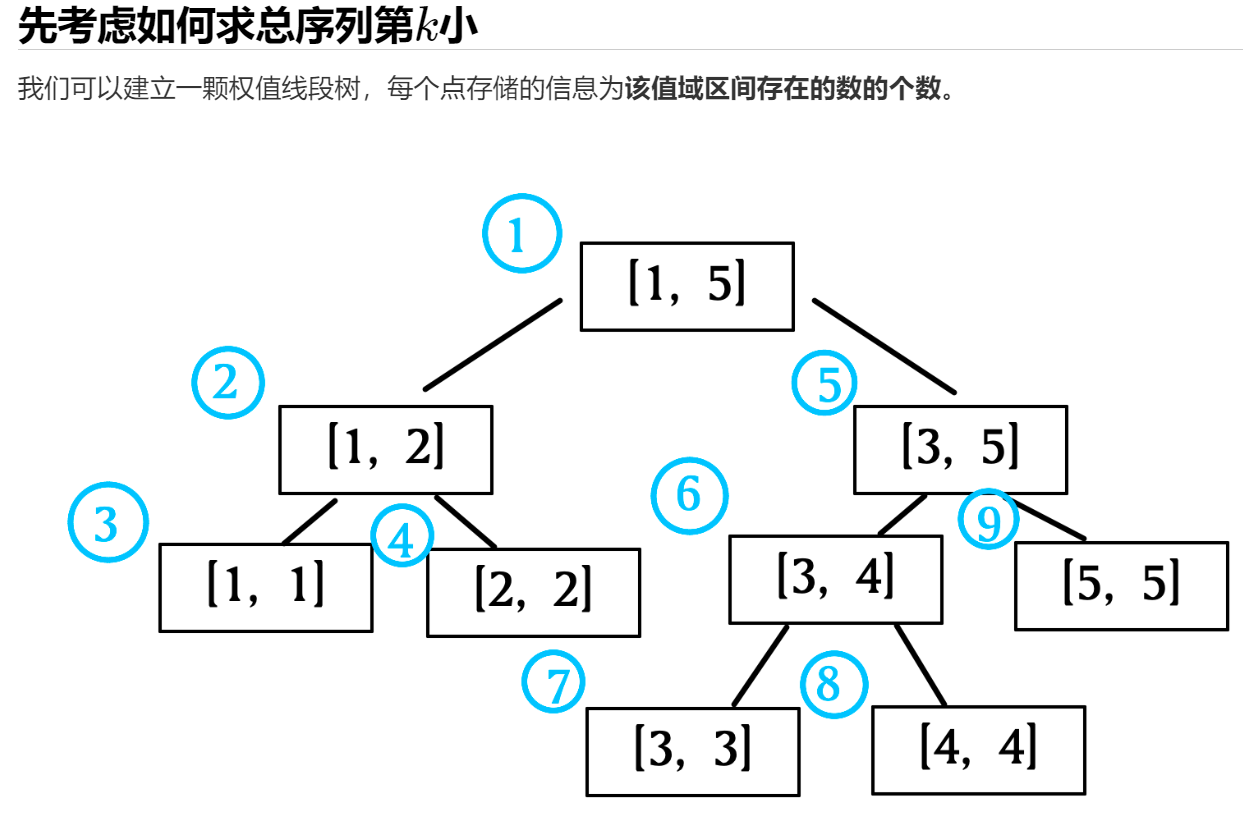
说远了，回到主席树：

这道题的线段树维护的数据是：这个区间中数出现的次数

对于每一个新加进序列的数，我们都要新开一个线段树

开始只建一个空线段树，后面不同通过加入新的数进入序列，从而根据这个空的线段树建立新的线段树

 

 

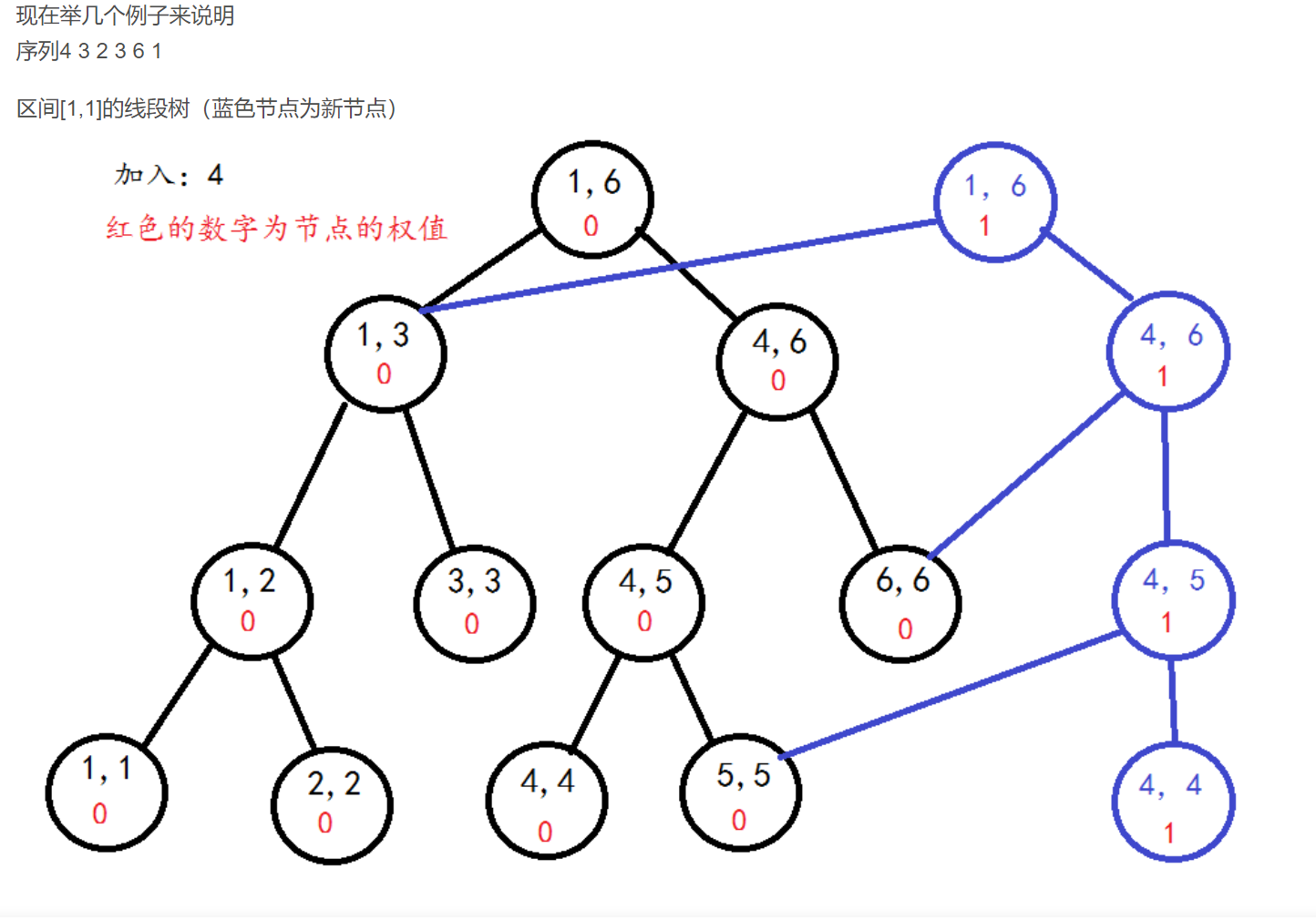
 每一个新的线段树，其根节点保存在roots[]中，在第i个线段树代表序列下标[1,i]中数的个数情况在线段树中的样子

 

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N = 100010, M = 10010;
struct tree
{
    // l,r是保存本节点的左右子节点在tr[]中的下标
    int l, r;
    //保存这一区间中的数的个数
    //带权线段树区间的含义是值域范围
    int cnt;
    //开5倍数组吧，不要问，问就是玄学
} tr[N << 5];
// tr[]的下标
int idx;
int a[N];
vector<int> nums;
//用来保存每个版本线段树的根节点
int roots[N];

// find函数返回在nums中不小于数x的下标位置
int find(int x)
{
    // lower_bound函数底层为二分，返回在数组中一个不小于x的位置
    return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
}

//既然是单点修改，那么就要用子节点更新父节点
void pushup(int u)
{
    tr[u].cnt = tr[tr[u].l].cnt + tr[tr[u].r].cnt;
}

//返回新建节点在tr[]中的下标
int build(int l, int r)
{
    int nidx = ++idx;
    if (l == r)
        return nidx;
    int mid = l + r >> 1;
    tr[nidx].l = build(l, mid);
    tr[nidx].r = build(mid + 1, r);
    return nidx;
}

//返回新开节点在tr[]中的下标位置
int insert(int last, int l, int r, int x)
{
    int nidx = ++idx;
    //先让本版本复制上一个版本
    tr[nidx] = tr[last];
    //接下来是对版本的更新
    if (l == r)
    {
        tr[nidx].cnt++;
        return nidx;
    }
    int mid = l + r >> 1;
    if (x <= mid)
        tr[nidx].l = insert(tr[last].l, l, mid, x);
    else
        tr[nidx].r = insert(tr[last].r, mid + 1, r, x);
    pushup(nidx);
    return nidx;
}

//返回在nums中的下标
//所谓的版本相减是版本中维护的信息相减
// l,r是维护的值域
// br,bl是两个版本的线段树在tr[]中所代表的下标
int query(int l, int r, int br, int bl, int k)
{
    if (l == r)
        return l;
    int cnt = tr[tr[br].l].cnt - tr[tr[bl].l].cnt;
    int mid = l + r >> 1;
    if (cnt >= k)
        return query(l, mid, tr[br].l, tr[bl].l, k);
    else
        return query(mid + 1, r, tr[br].r, tr[bl].r, k - cnt);
}

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        // a[]是真正的原数据
        // nums是用来离散化的数据
        scanf("%d", &a[i]);
        nums.push_back(a[i]);
    }
    sort(nums.begin(), nums.end());
    // unique是对已经排序的数组进行去重操作,并返回去重数组后的最后下标（指针形式）
    // erase是删除下标（指针形式）a->b的全部元素
    nums.erase(unique(nums.begin(), nums.end()), nums.end());

    //离散化后的数组nums大小为tr[]节点的区间,对于一个数x,我们
    //等下要用find(x)找到,数x在nums中的位置;
    // build操作只是建了个空树而已,方便insert建立新版本线段树
    roots[0] = build(0, nums.size() - 1);

    //开始建立新版本线段树
    //每一个版本i代表：a[]数组中下标1~i区间，在线段树中的区间中数的个数
    for (int i = 1; i <= n; i++)
        // roots[i-1]表示上一个版本,因为这个版本是以上个版本为样例
        //进行改变,线段树初始范围0，nums.size()-1,
        //上一个版本是1~a[i-1],这个版本是要1~a[i],
        // find(a[i])找到数a[i]要插进线段树哪一个范围,相当于单点修改
        roots[i] = insert(roots[i - 1], 0, nums.size() - 1, find(a[i]));

    while (m--)
    {
        int l, r, k;
        scanf("%d%d%d", &l, &r, &k);
        printf("%d\n", nums[query(0, nums.size() - 1, roots[r], roots[l - 1], k)]);
    }
    return 0;
}