数论----余数

《模运算》

 《性质》

 《同余》

更好理解的方式是：我们将除以同一个数，得到余数相同的数，称为同余关系

我们将除以同一个数，得到余数相同的数，称为同余关系

设 a=nq+r,b=nq′+r(n,q,q′,r∈N,r<n) 因为 a mod n=r,b mod n=r

则a与b 同余，记为  a≡b(mod n),也可以记为 b≡a(mod n)

《性质》

一般的证明都可以由 a=nq+r, b=nq′+r推导出来

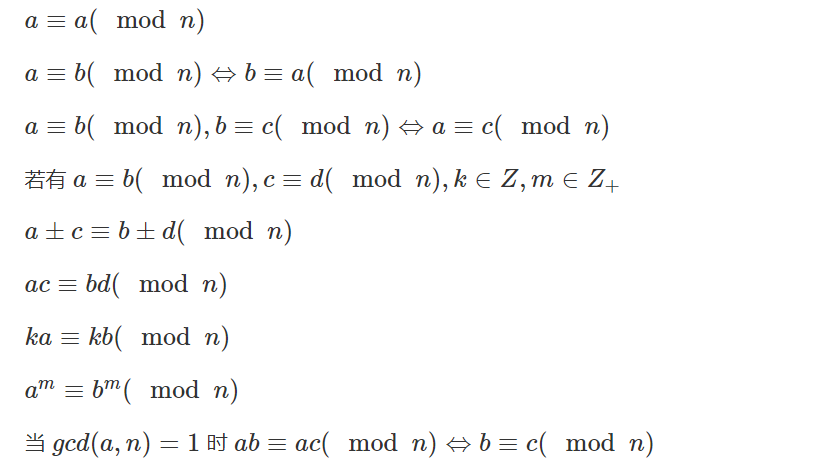
 比如证明最后一条性质：

　　设：ab=k1*n+r　　ac=k2*n+r

　　因为 a与n互质

　　则：b=(k1/a)*n+r/a　　c=(k2/a)*n+r/a

　　k1/a与k2/a均为整数，则可不管，照样b与c同余

《同余类（剩余类）》

 

 《性质》

 

 《完全剩余系》

《简化完全剩余系》