并查集

《种类并查集》

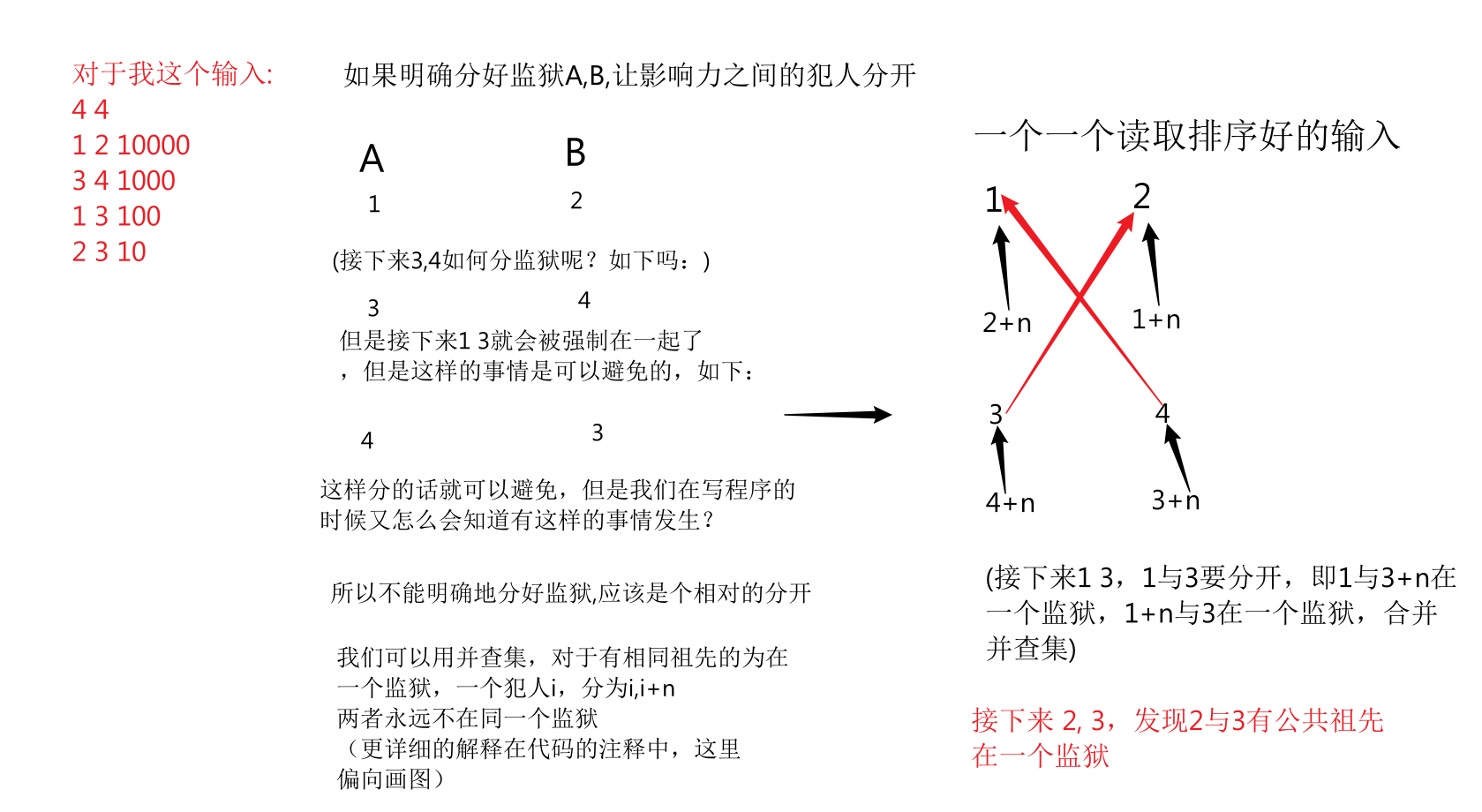
对于不能一个并查集不够用了，还需要另一个并查集，但是不能开两个数组作为两个并查集，因为两个并查集之间不能有明确的区分

以样例说明：

 

 

 

贪心思路：

很容易便能想到，我们要使怒气值大的一对人尽量不在同一间监狱里。也就是说，我们要优先考虑怒气值最大的两个人，然后是次大，以此类推。这一想法很容易证明，即用交换法。

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 200000;
// a 表示并查集
// hate表示两个犯人之间的关系
struct node
{
    int l, r, w;
} hate[N];
int a[N * 2];
int n, m;
//返回x的祖先是谁
int find(int x)
{
    if (a[x] != x)
        a[x] = find(a[x]);
    return a[x];
}
//合并,本题即关进相同监狱
void merge(int x, int h)
{
    a[find(h)] = find(x + n);
    a[find(h + n)] = find(x);
}
int main()
{
    cin >> n >> m;
    //初始化并查集
    for (int i = 1; i <= n * 2; i++)
        a[i] = i;
    for (int i = 1; i <= m; i++)
        scanf("%d%d%d", &hate[i].l, &hate[i].r, &hate[i].w);
    sort(hate + 1, hate + m + 1, [](struct node a, struct node b)
         { return a.w > b.w; });
    //这道题绝对不能指明清楚的监狱关系
    //即不能说犯人1进A监狱,犯人2进B监狱,这样明确的
    //要不论A,B监狱怎么变化都不影响影响力

    //!!!注意我们规定:有共同祖先说明两者在同一个监狱

    //如果对于犯人i,其有两个分身，一个是i,一个是i+n
    //当i分监狱时,如果i进A监狱，i+n就要进B监狱
    //如果i进B监狱，i+n就要进A监狱,即i,i+n是永远不会在同一个监狱
    //并且A,B监狱不管如何变换,i与i+n的关系不会变

    //到后面如果犯人i+k与犯人i有排在更前面的影响力
    //首先判断犯人i+k与犯人i在贪心下是否被强制在一个监狱
    //即判断if(find(a[i+k])==find(a[i])),即判断是否是共同祖先
    //如果是则可以退出整个算法,i+k与i之间的影响力就是最大影响力中的最小了;
    //如果不在则进行如下一步:

    //则i+k要与i分开监狱
    //即要将i+k与i+n合并,因为i与i+n永远不会在同一个监狱，这是规定
    //同时i与i+k+n合并
    //即a[find(i+k)]=find(i+n); a[find(i+k+n)]=find(i);

    //对于下一个关系重复上述步骤
    int res = 0;
    for (int i = 1; i <= m; i++)
    {
        auto t = hate[i];
        if (find(t.l) == find(t.r))
        {
            res = t.w;
            break;
        }
        merge(t.l, t.r);
    }
    cout << res;
}