运用倍增思想实现RMQ（RMQ (Range Minimum/Maximum Query)）问题

本博客大部分是我对这位大佬的文章的个人理解：https://blog.csdn.net/weixin_45697774/article/details/105289810

《倍增》

 

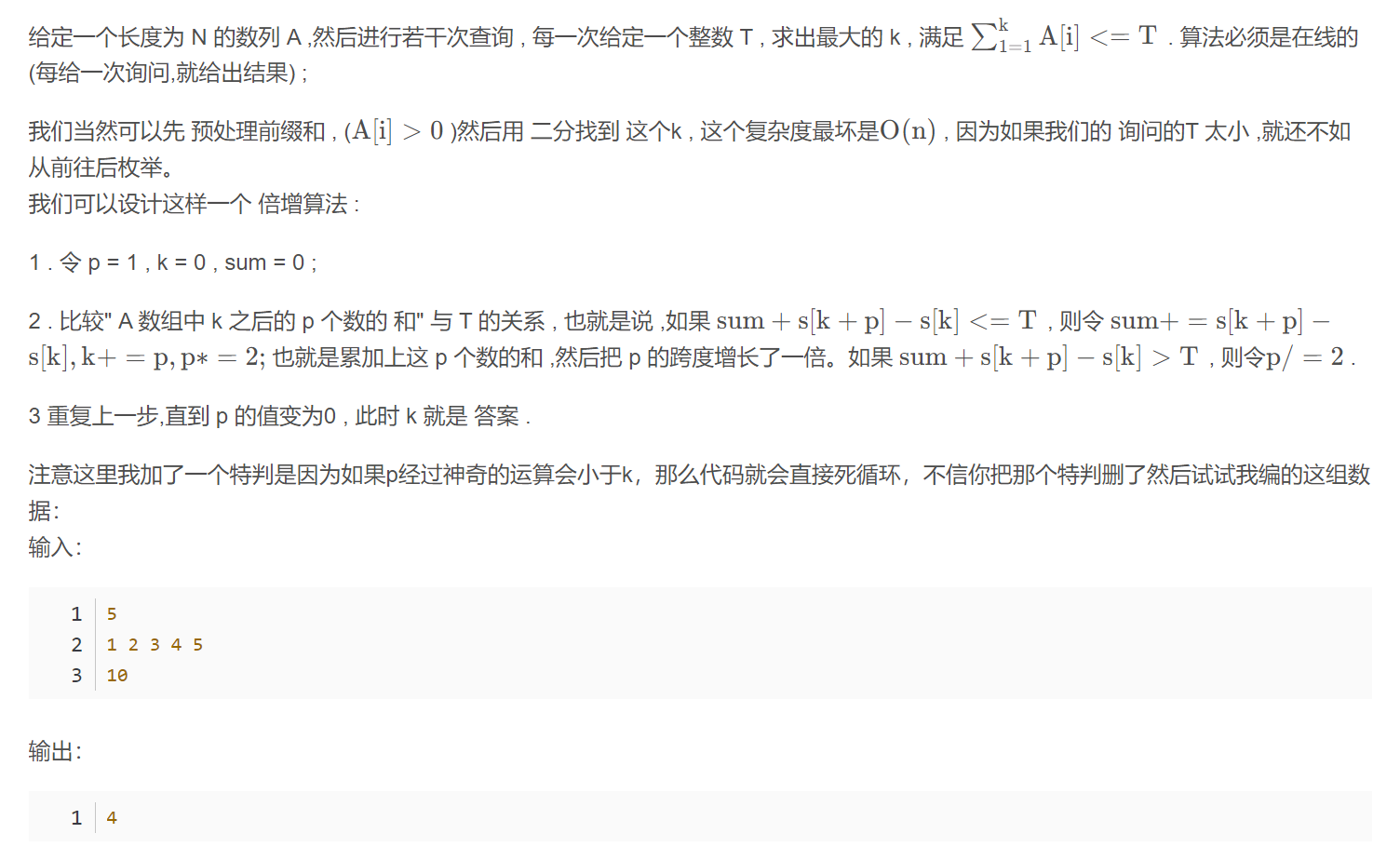
 《RMQ问题》

 

 对于这道题：

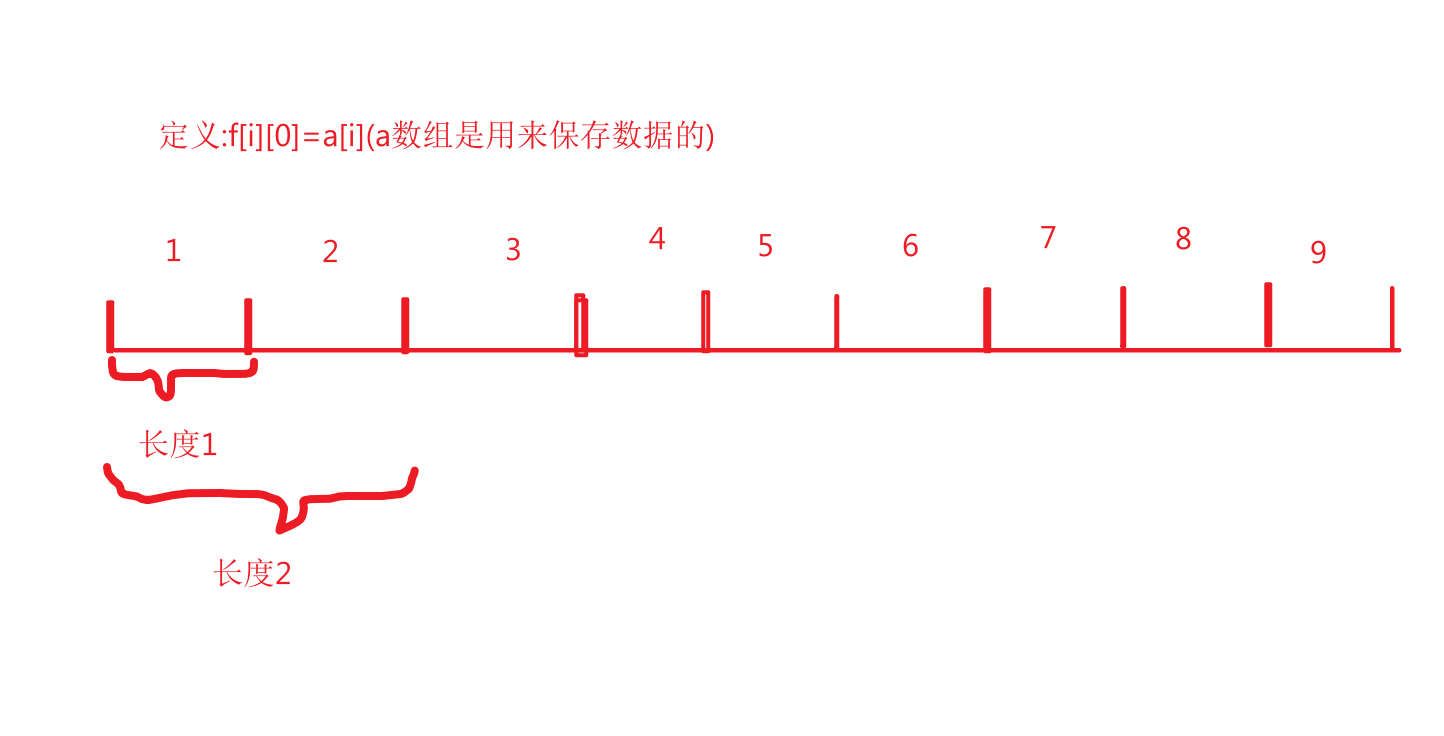
　　（这个f数组被称为ST表）

　　1.首先定义一个数组 f[N][logN+1],这个数组f[i][j]表示在点i出往后2^j个长度内，即[i,i+2^j]的区间中的最大值为f[i][j];

　　

　　2.对于给出的区间询问[l,r],如何求出其中最大值呢?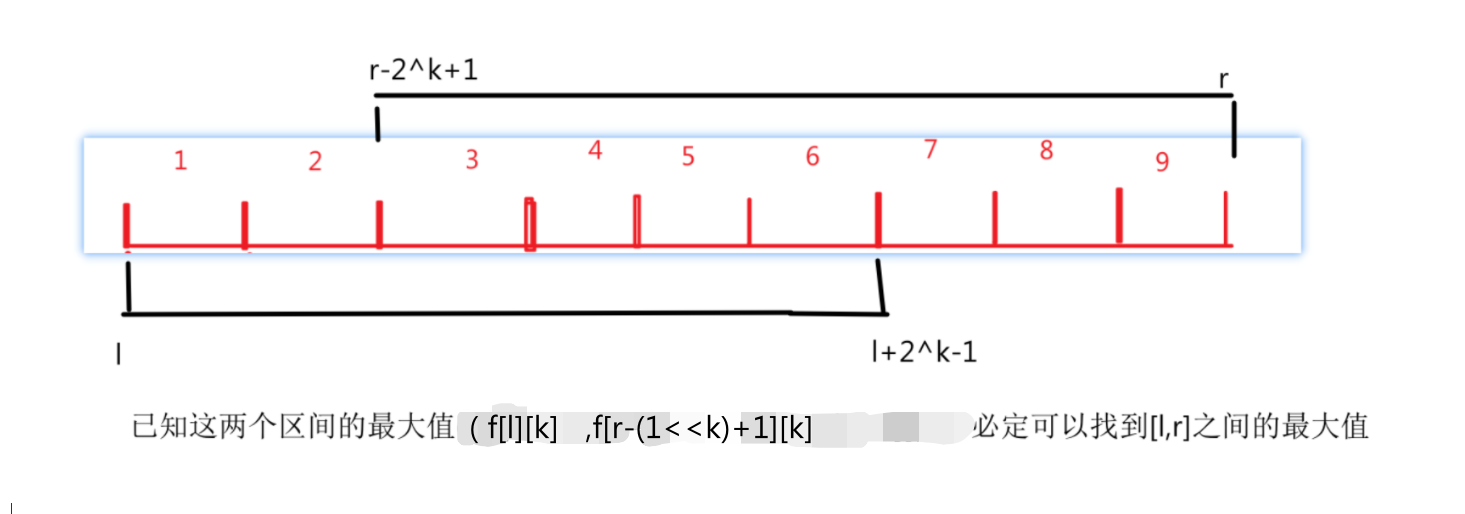

k又是如何取的呢？

　　k=log(r-l+1)/log(2);

　　l+2^k-1<=r, l+2^(k+1)-1>r

　　r-2^k+1>=l, r-2^(k+1)-1<l

　　3.如何求f[i][j]?

 

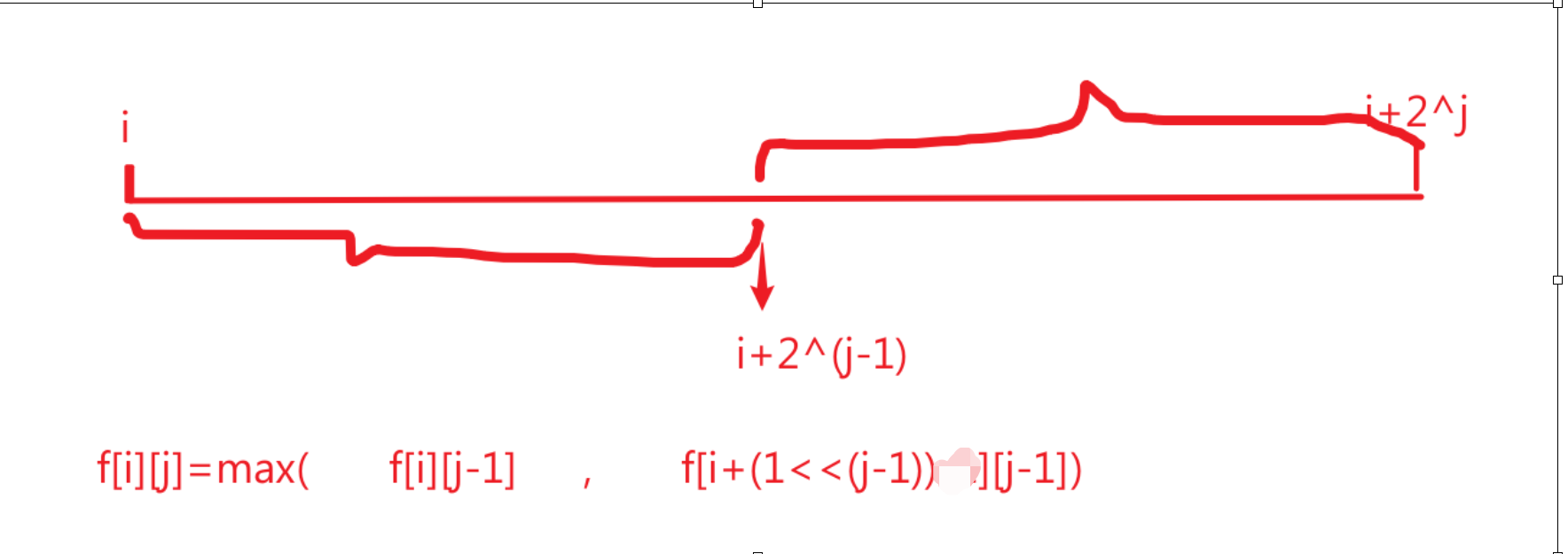
 可知：正如dp一样，可以推出来

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 200010;
// 17<logN 18>logN;
int a[N], f[N][18];
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);

    //开始处理f数组，f[i][j]:表示在点i处往后2^j的长度范围内的区间最大值
    //即[l,l+2^j]的最大值
　　　　//时间复杂度O（nlogn）

    for (int i = n; i >= 1; i--)
    {
        f[i][0] = a[i];
        for (int j = 1; i + (1 << j) - 1 <= n; j++)
            f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
    }
    int m;
    cin >> m;
    while (m--)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        //开始通过ST表（f数组）查找答案:
        int len = r - l + 1;
        int k = log(len) / log(2);
        int ans = max(f[l][k], f[r - (1 << k) + 1][k]);
        cout << ans << endl;
    }
    return 0;
}