欧拉函数

 

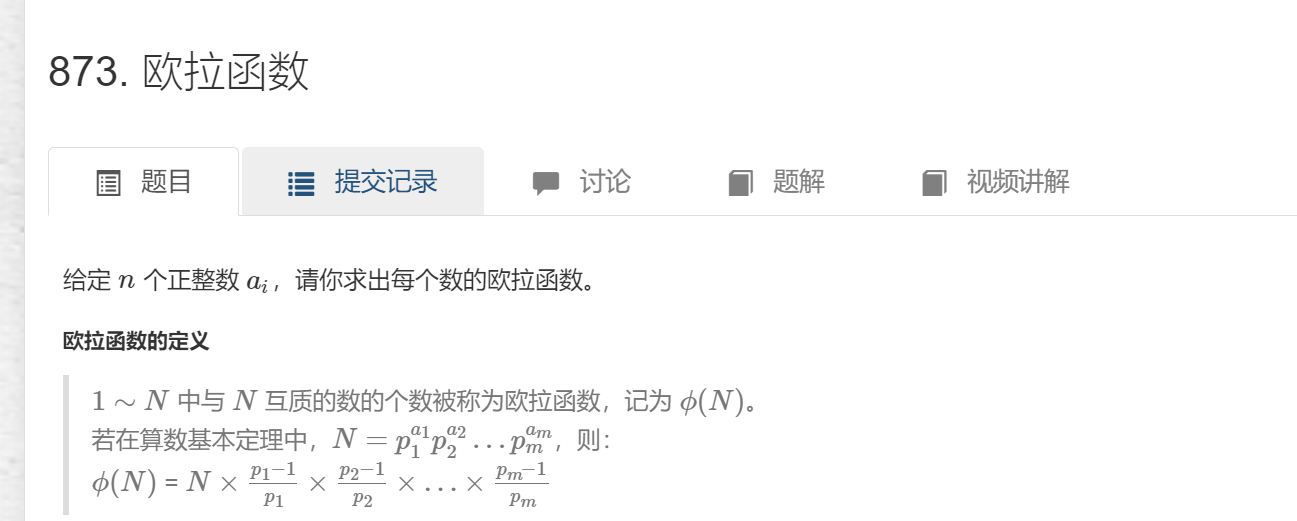
 在N=p1^a1*p2^a2*...*pm^am中p是质因数，a是指数；如   24=2^3*3^1；

 

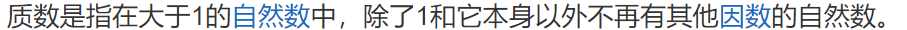
 即 Q(N)=N*(1-1/p1)*(1-1/p2)*...*(1-1/pm);

这里如果用欧几里得算法(即辗转相除法)gcd()，从1开始一个一个数与N算，光是O（100*2*1e9）就会超时；

所以这里要用到欧拉函数

《证明》

这里要用到容斥原理

 

 

 

 

 

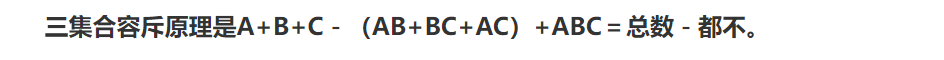
 如何求1~N中，与N互质的个数？

最朴实的做法是：N - 与N有公约数的数的个数

 在1~N 中 p1的倍数个数是N/p1（一定是整除才行），同理 pi的倍数个数是N/pi;

第一步：

　　从1~N中去掉p1,p2...pk的所有倍数：N-N/p1-N/p2-...N/pk;

但是发现有些数即是pi的倍数也是pj的倍数，但是这些数我本来只要减去1次，但是上面的减去了2次

所有

第二步：

　　从1~N中加上是pi*pj的倍数的个数：N-N/p1-N/p2-...N/pk   + N/p1*p2+N/p1*p3+....+N/pk-1*pk;

但是又发现有些数 即是pi的倍数 也是pj的倍数，也是pk的倍数；但在+N/pi*pj+N/pi*pk+N/pj*pk中我加了3次

但是这些数我本来才上面-N/pi-N/pj-N/pk

相当于这些数即没加也每减

所以：

第三步：

　　从1~N中减去是pi*pj*pk的倍数的个数:

................

按照这个规则+二项式展开：Q(N)=N*(1-1/p1)*（1-1/p2）*....*(1-1/pm)

《代码》

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        int num, ans;
        cin >> num;
        ans = num;
        for (int i = 2; i <= num / i; i++)
        {
            if (num % i == 0)
            {
                while (num % i == 0)
                    num /= i;
　　　　　　　　　　　//注意这里还是挺有讲究的
　　　　　　　　　　　//不能写成ans=ans*(i-1)/i,因为可能i很大，ans*(i-1)之后就爆int了

                ans = ans / i * (i - 1);
            }
        }
        if (num > 1)
            ans = ans / num * (num - 1);
        cout << ans << endl;
    }
    return 0;
}

 《筛法求1~n中的欧拉函数之和》

 

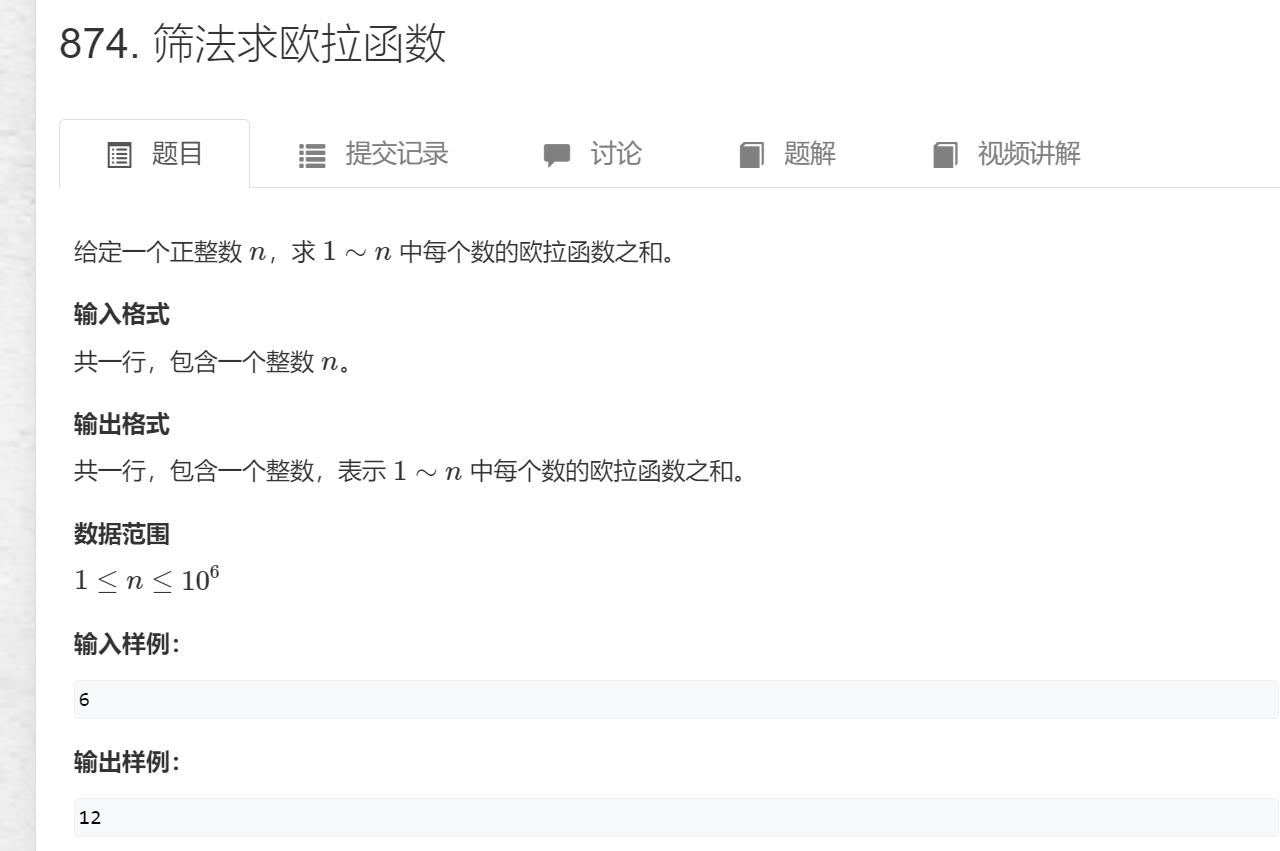
 普通做法循环n个数，对于每个数求分解质因数，总时间复杂度O（n^2）,超时

利用线性筛的思想，O（n）时间内可解出:

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
//保存每一个数的欧拉函数
int phi[N], primes[N], cnt = 0;
bool st[N];
LL get_eulers(int n)
{
    memset(st, false, sizeof(st));
    phi[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
        {
            primes[cnt++] = i;
            //下面都是对合数的处理,这里处理质数
            phi[i] = i - 1; //==i*(1-1/i)
        }
        for (int j = 0; primes[j] <= n / i; j++)
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0)
            {
                //能进这里说明i是个合数,primes[j]是其最小质因数
                // Q(i)=i*(1-1/p1)*(1-1/p2)*...*(1-1/pk);其中一定包含(1-1/primes[j]);
                // Q(primes[j])=primes[j]*(1-1/primes[j]);
                // Q(i*primes[j])=i*primes[j]*(1-1/p1)*(1-1/p2)*...*(1-1/pk);
                // Q(i*primes[j])==Q(i)*primes[j];
                phi[i * primes[j]] = phi[i] * primes[j];
                break;
            }
            //没进入上面的语句说明primes[j]不是i的质因数
            // Q(i)=i*(1-1/p1)*(1-1/p2)*...*(1-1/pk);其中一定不包含(1-1/primes[j]);
            // Q(primes[j])=primes[j]*(1-1/primes[j]);
            // Q(i*primes[j])=i*primes[j]*(1-1/p1)*(1-1/p2)*...*(1-1/pk);其中一定包含(1-1/primes[j]);
            // Q(i*primes[j])==Q(i)*Q(primes[j]);
            phi[i * primes[j]] = phi[i] *(primes[j]-1);
        }
    }
    LL res = 0;
    for (int i = 1; i <= n; i++)
        res += phi[i];
    return res;
}
int main()
{
    int n;
    cin >> n;
    cout << get_eulers(n);
    return 0;
}