莫队----十分适合处理离线的区间问题

 

 所谓离线的意思是指:先读取全部的输入，经过算法的一系列操作，最后在按照读入的顺序输出答案

相对的，在线的意思是：读取一行输入，输出一行对应的答案

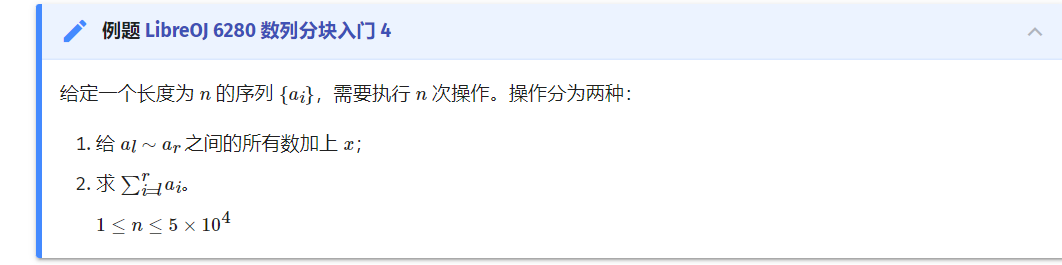
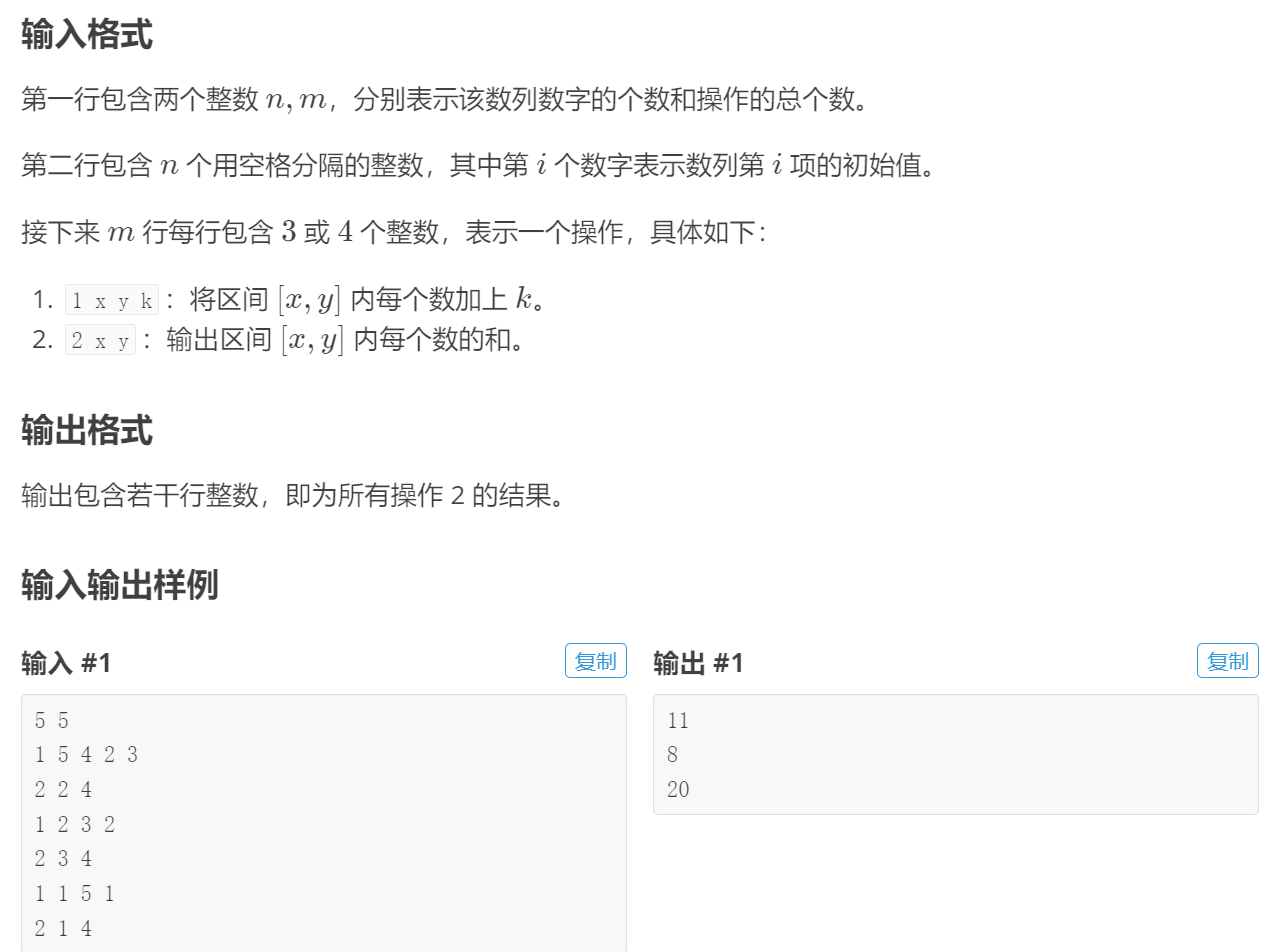
《分块》

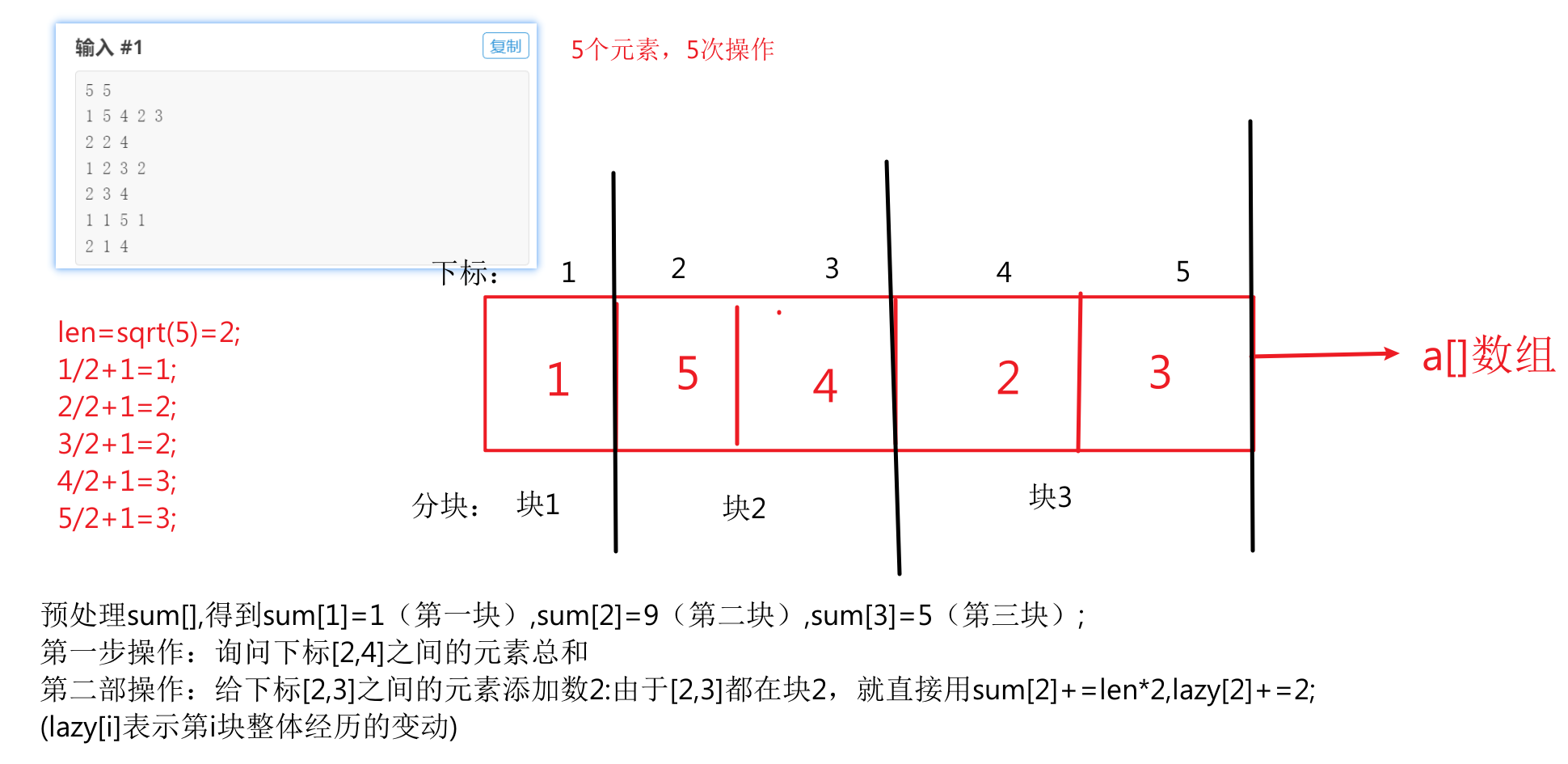
由于莫队的核心思想是分块，所以先说一下分块这个思想：

 

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n, m;
int a[N], sum[N], lazy[N], len;
　　//分块后，对于下标x，求出其所在的块号
int get(int x)
{
    return x / len + 1;
}
void update(int l, int r, int k)
{
    int q = get(l), p = get(r);
    //同一块
    if (q == p)
    {
        for (int i = l; i <= r; i++)
            sum[q] += k, a[i] += k;
        return;
    }
    //不同块
    //先处理在相同块中的:
    for (int i = q + 1; i <= p - 1; i++)
    {
        sum[i] += len * k;
        // lazy[i]数组记录的是在整个第i块中受到的改变，
        //如果没有lazy[]数组那么当整块受到改变时，就要遍历这一整块
　　　　　　　//所以在下面求和过程中也要记得加上lazy[]数组
        lazy[i] += k;
    }
　　　　//右边离散的元素的改变
    for (int i = l; get(i) == q; i++)
    {
        sum[q] += k;
        a[i] += k;
    }
　　　　//左边离散的元素的改变
    for (int i = r; get(i) == p; i--)
    {
        sum[p] += k;
        a[i] += k;
    }
}
LL ask(int l, int r)
{
    LL res = 0;
    int q = get(l), p = get(r);
    if (q == p)
        for (int i = l; i <= r; i++)
            res += (a[i] + lazy[q]);
    else
    {
        //先处理同块:
        for (int i = q + 1; i <= p - 1; i++)
            res += sum[i];
        for (int i = l; get(i) == q; i++)
            res += (a[i] + lazy[q]);
        for (int i = r; get(i) == p; i--)
            res += (a[i] + lazy[p]);
    }
    return res;
}
int main()
{
    cin >> n >> m;
    //分组
    len = sqrt(n);//获得每一块长度
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
　　　　　　//sum[i]代表在第i块的元素总和为sum[i];
        sum[get(i)] += a[i];
    }
    int op, l, r, k;
    while (m--)
    {
        cin >> op >> l >> r;
        if (op == 1)
        {
            cin >> k;
            update(l, r, k);
        }
        else
            cout << ask(l, r) << endl;
    }
    return 0;
}

 

 

 《普通莫队》

 还是上面的题目：

 

 

 知道上面的方法后，如果我已经知道了在区间[l,r]的值，为了求其他区域的值我可以如下操作：

 

 

 说明：比如我知道了在区间[3,5]的和，求[2,5]的和，这时应该用Add(--3)==Add(2),同时l=2;

求[4,5]的和，这时应该Sub(3++)==Sub(3),同时l=4;

如果我们像上面那样操作，则：

 

 

 所以我们要离线操作，首先读入全部的输入，然后对输入排序

加上我们的分块操作，有排序的原则：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 5 * 1e4 + 10;
int n, m, k;
int a[N], pos[N], ans[N]；　　　　　　// pos记录序号i在第几块，ans[i]记录第i次输入时的答案；
int res;                          //res全局维护的[l,r]之间的答案;
struct Q
{
    int l, r, k;
} q[N];//记录输入的信息
void add(int x)
{
  //不同题目不一样18 }
void sub(int x)
{
   //不同题目不一样23 }
int main()
{
    cin >> n >> m >> k;
    //分块
    int len = sqrt(n);
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        pos[i] = i / len + 1;
    }

    for (int i = 1; i <= m; i++)
    {
        cin >> q[i].l >> q[i].r;
　　　　　　　//记录一下这个读入是第几个读入，好按读入顺序输出
        q[i].k = i;
    }

　　//将提问按照排序规则排序
    sort(q + 1, q + m + 1, [](Q x, Q y)
         { return pos[x.l] == pos[y.l] ? x.r < y.r : pos[x.l] < pos[y.l]; });
　　　　
　　　　//这样初始化很有讲解
    int l = 1, r = 0; //维护双指针，[l,r]这个范围的答案我们是知道的；
    for (int i = 1; i <= m; i++)
    {
        while (q[i].l < l)
            add(--l);
        while (q[i].l > l)
            sub(l++);
        while (q[i].r > r)
            add(++r);
        while (q[i].r < r)
            sub(r--);
        ans[q[i].k] = res;
    }
    for (int i = 1; i <= m; i++)
        cout << ans[i] << endl;
    return 0;
}

对于这个题目：

开一个数组cnt[]，cnt[i]表示数i在区间[l,r]上一共出现了cnt[i]次
1 void add(int x)
{
    cnt[a[x]]++;
    res += (cnt[a[x]] * cnt[a[x]]) - (cnt[a[x]] - 1) * (cnt[a[x]] - 1);
}
void sub(int x)
{
    cnt[a[x]]--;
    res -= (cnt[a[x]] + 1) * (cnt[a[x]] + 1) - (cnt[a[x]]) * (cnt[a[x]]);
}

 时间复杂度：在n元素长度与m操作次数，阶数相同的情况下为O（nsqrt(n)）;