动态规划----背包问题

《最初始的01背包问题》

 

 让我们用暴力搜索试一试：

int dfs(int i,int j){}

这个函数的作用是：返回在前i个物品中选，体积不超过j的能得到的最大价值；

1 int dfs(int i,int j)
2 {
3     int res;
4     if (i==0)res=0;
5     if (j<w[i]) res=dfs(i-1,j);
6     else res=max(dfs(i-1,j),dfs(i-1,j-w[i])+v[i]);
7     return res; 
8 }

会发现可能有重复计算，比如：dfs(1,5)可能会计算好几遍

优化：

定义一个数组：dp[][];

int dfs(int i, int j)
{
    if (dp[i][j]!=-1) return dp[i][j];
    int res;
    if (i == 0)
        res = 0;
    if (j < w[i])
        res = dfs(i - 1, j);
    else
        res = max(dfs(i - 1, j), dfs(i - 1, j - w[i]) + v[i]);
    return dp[i][j]=res;
}

然后可以将dp[][]用非递归的形式写出

for (int i = 1; i <= n; i++)
{
    for (int j = 0; j <= m; j++)
    {
        if (j < w[i])
            dp[i][j] = dp[i - 1][j];
        else
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
    }
}

初始化：
根据dp的定义来：dp[i][j]在前i件物品中选择总体积不大于j的最大价值
一般在背包问题中初始化只考虑再第0件物品的情况
即要考虑dp[0][0~m]的初始值
根据定义：dp[0][0]在前0件物品中选择总体积不大于0的最大价值肯定为0
dp[0][j]在前0件物品中选择总体积不大于j的最大价值肯定为0

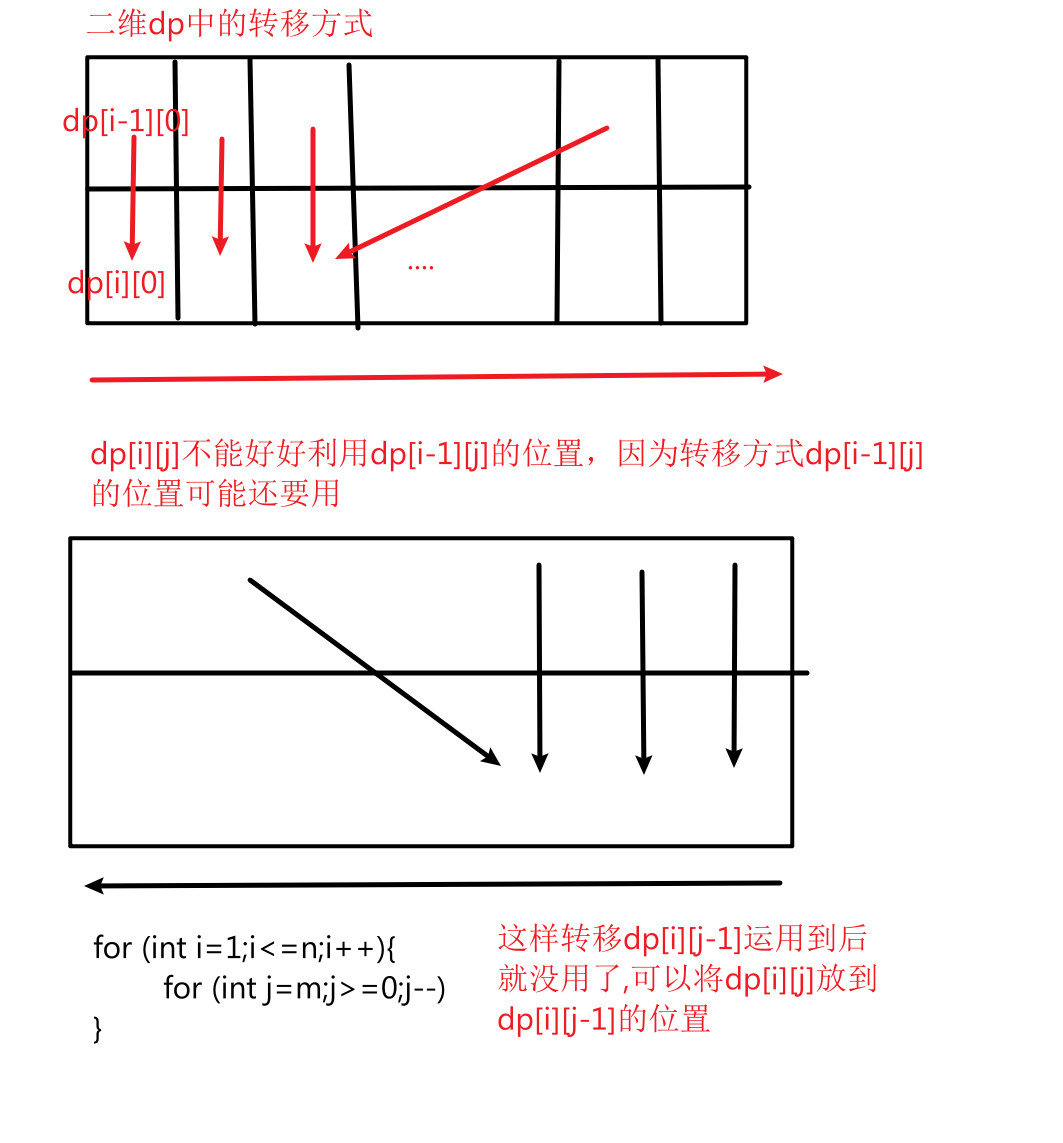
《滚动数组优化》

for (int i=1;i<=n;i++)
{
    for (int j=m;j>=w[i];j--)
        dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}

为啥不是for (int j=m;j>=0;j--) ,因为在j<w[i]时，是直接dp[i][j]=dp[i-1][j]，这里改成一维后，dp[j]=dp[j]也没必要了

《背包问题求方案数》

 

 如果说上面的01背包问题给出限制是不大于j

那么这里是恰好为j

即：从前i个物品中选，体积恰好为j的方案数

由题意：dp[0][0]=1,什么都不选为1种方案；dp[0][j]=0,从前0个物品中选，体积恰好为j的方案数,根本不可能由这种方案，即dp[0][j]=0;

而且dp[i][j]=dp[i-1][j]+dp[i-1][j-w[i]];

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int M = 10010;
int n, m, dp[110][M];
int main()
{
    cin >> n >> m;
    int num;
    dp[0][0] = 1;
    for (int i = 1; i <= n; i++)
    {
　　　　　//这样写就不用开一个数组来记录数了
        cin >> num;
        for (int j = 0; j <= m; j++)
        {
            dp[i][j] += dp[i - 1][j];
            if (j >= num)
                dp[i][j] += dp[i - 1][j - num];
        }
    }
    cout << dp[n][m];
    return 0;
}

 《背包问题求具体方案数》

 

 这里以01背包为例：

　　求具体方案数问题其实对应着求一个最短路问题

 

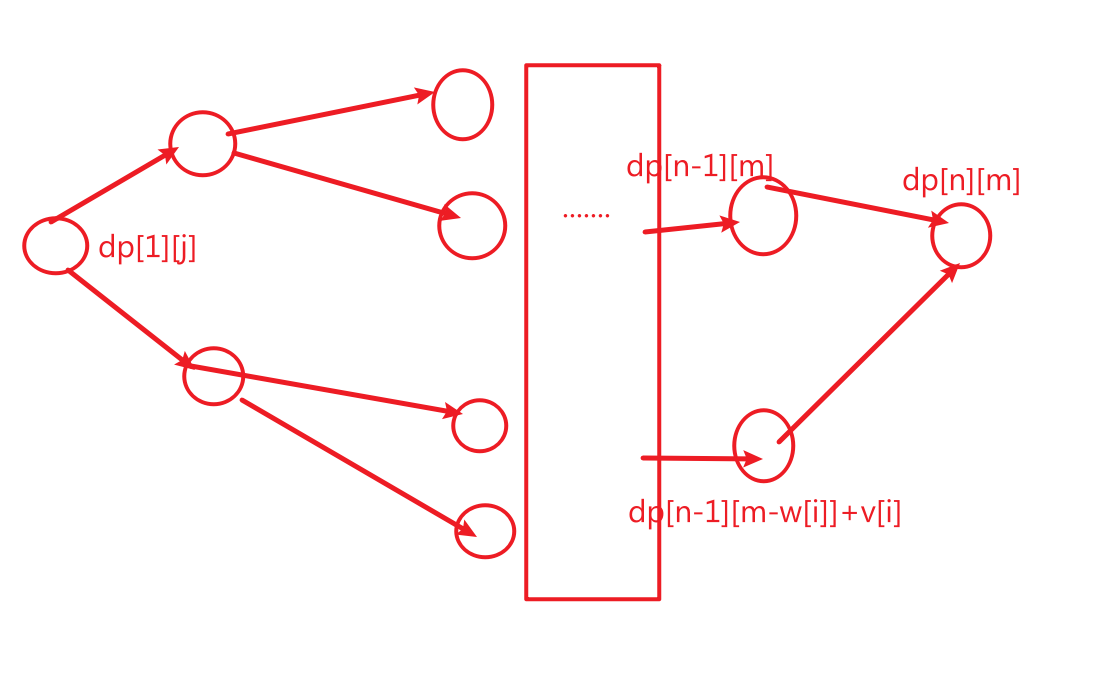
对于每一个状态如何判断其是从那个状态转移过来的？以dp[n][m]为例;

if dp[n][m]==dp[n-1][m] 说明dp[n][m]这个状态是从dp[n-1][m]转移过来的

if dp[n][m]==dp[n-1][m-w[i]]+v[i] 说明dp[n][m]这个状态是从dp[n-1][m-w[i]] 转移过来的

 

但是这里是按照字典序来输出的,上述的判断方式是从n->1进行判断

但应该从1开始判断到n

以物品1为案例:

　　当物品1可有可无时：一定要选，可以保证字典序最小

　　当物品1一定要选时：选

　　当物品1一定不能选时：不选

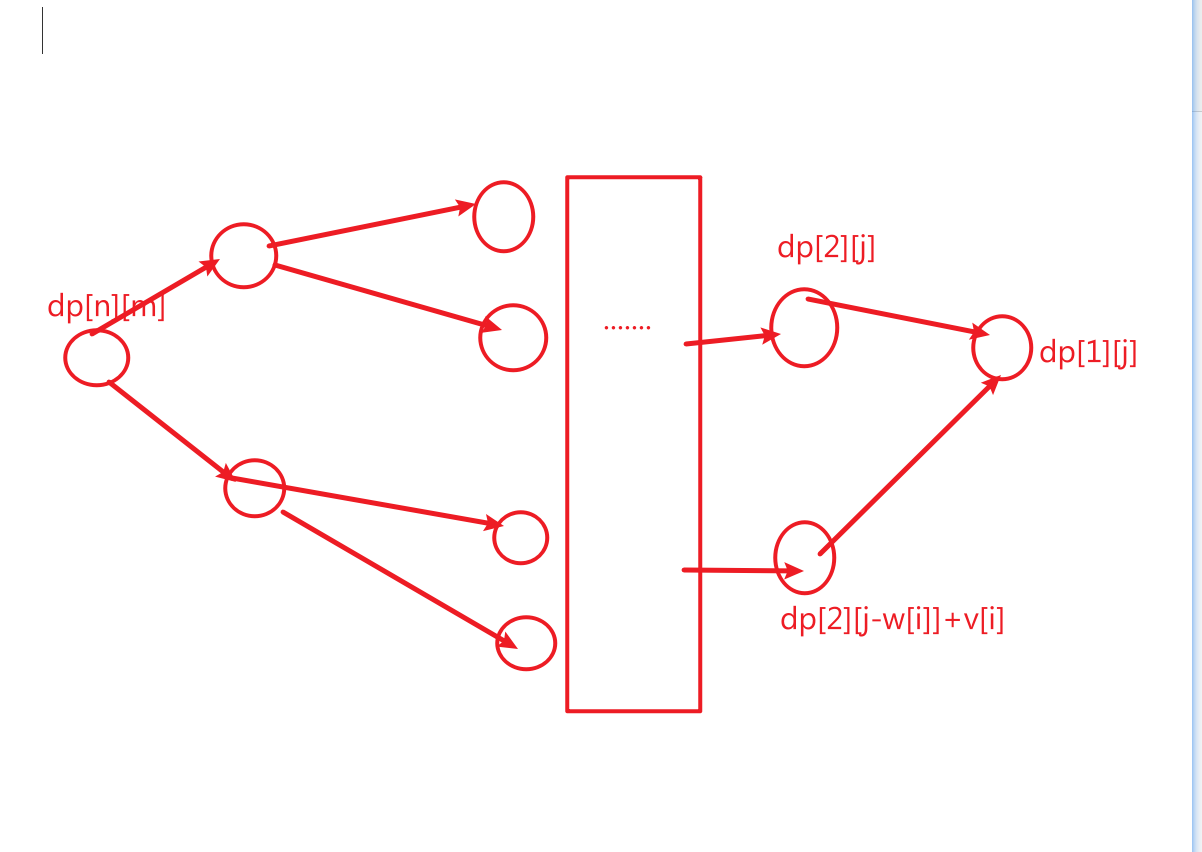
即让状态转移为：dp[i][j]=max(dp[i][j],dp[i+1][j-w[i]]+v[i]);

变成如下：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
int v[N], w[N], dp[N][N];
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> w[i] >> v[i];
    // dp[i][j]的含义是从后第i个物品开始选,总体积不超过j,一直选道最后一件物品的最大价值；
    // 明显dp[n+1][j]=0;
    for (int i = n; i >= 1; i--)
    {
        for (int j = 0; j <= m; j++)
        {
            dp[i][j] = dp[i + 1][j];
            if (j >= w[i])
                dp[i][j] = max(dp[i][j], dp[i + 1][j - w[i]] + v[i]);
        }
    }
　　　　//开始寻找
    int j = m;
    for (int i = 1; i <= n; i++)
    {
        if (j >= w[i] && dp[i][j] == dp[i + 1][j - w[i]] + v[i])
        {
            cout << i << " ";
            j -= w[i];
        }
    }
    return 0;
}