Dfs

《dfs的连通块模型》

这种题目大多是既可以用bfs也可以用dfs来解决的，其实在图的内部进行搜索遍历，对于dfs来说

这种模型不用恢复现场（即回溯）

《dfs的状态转移模型》

这种题目一般是一次变换之后，以整个图的状态为单位进行转换，这时就要恢复现场、

《dfs之搜索顺序》

这种题目即要找到一种搜索顺序使可以在爆搜的情况下能遍历到全部的状态

 1 1117. 单词接龙
 2 
 3 单词接龙是一个与我们经常玩的成语接龙相类似的游戏。
 4 
 5 现在我们已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”，每个单词最多被使用两次。
 6 
 7 在两个单词相连时，其重合部分合为一部分，例如 beast 和 astonish ，如果接成一条龙则变为 beastonish。
 8 
 9 我们可以任意选择重合部分的长度，但其长度必须大于等于1，且严格小于两个串的长度，例如 at 和 atide 间不能相连。
10 
11 输入格式
12 输入的第一行为一个单独的整数 n 表示单词数，以下 n 行每行有一个单词（只含有大写或小写字母，长度不超过20），输入的最后一行为一个单个字符，表示“龙”开头的字母。
13 
14 你可以假定以此字母开头的“龙”一定存在。
15 
16 输出格式
17 只需输出以此字母开头的最长的“龙”的长度。
18 
19 数据范围
20 n≤20
21 输入样例：
22 5
23 at
24 touch
25 cheat
26 choose
27 tact
28 a
29 输出样例：
30 23
31 提示
32 连成的“龙”为 atoucheatactactouchoose。

注意点：

1.每个单词最多被使用两次，说明单词可以重复，这时以前传统的 bool st[]数组要改成，int used[],用来记录使用次数

2、为了最长那么重合的地方取最小，而且计算最小重合长度肯定要预处理，不能放在dfs中再一个一个求；

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 using namespace std;
 5 const int N = 21;
 6 string words[N];
 7 int used[N], g[N][N];
 8 int n, ans;
 9 char start;
10 void dfs(string dargon, int x)
11 {
12     if (ans < dargon.size())
13         ans = dargon.size();
14     used[x]++;
15     for (int i = 0; i < n; i++)
16     {
17         if (g[x][i] && used[i] < 2)
18         {
19             /*dargon=dargon + words[i].substr(g[x][i]);//我代码这里是错误的
　　　　　　　　　　//因为如果我这样写dargon在下面也要恢复现场，很麻烦，所以这里要写成:
20             dfs(dargon, i);*/
　　　　　　　　  dfs(dragon + word[i].substr(g[x][i]), i); 
21         }
22     }
23     used[x]--;
24 }
25 int main()
26 {
27     cin >> n;
28     for (int i = 0; i < n; i++)
29         cin >> words[i];
30     cin >> start;
31     //预处理一下两个单词最小的可连接长度
32     for (int i = 0; i < n; i++)
33     {
34         for (int j = 0; j < n; j++)
35         {
36             string a = words[i], b = words[j];
37             for (int k = 1; k < min(a.size(), b.size()); k++)
38             {
39                 if (a.substr(a.size() - k, k) == b.substr(0, k))
40                 {
41                     g[i][j] = k;
42                     break;
43                 }
44             }
45         }
46     }
47     for (int i = 0; i < n; i++)
48     {
49         if (words[i][0] == start)
50             dfs(words[i], i);
51     }
52     cout << ans;
53     return 0;
54 }

《dfs的搜索原理与精髓》

1.dfs首先要想到一个搜索方式，能够将全部的情况都不漏地搜索到（可以重复，当然越少重复越好）

尽量让决策的分支少

2.然后画出dfs的搜索顺序的搜索树，根据树进行递归写代码，逻辑更加清晰（其实递归的搜索顺序与这颗数的前序遍历是一样的）

如何建树？技巧是：只要决策了，就进行递归一层

3.尽量优化（剪枝）

《递归实现指数型枚举》

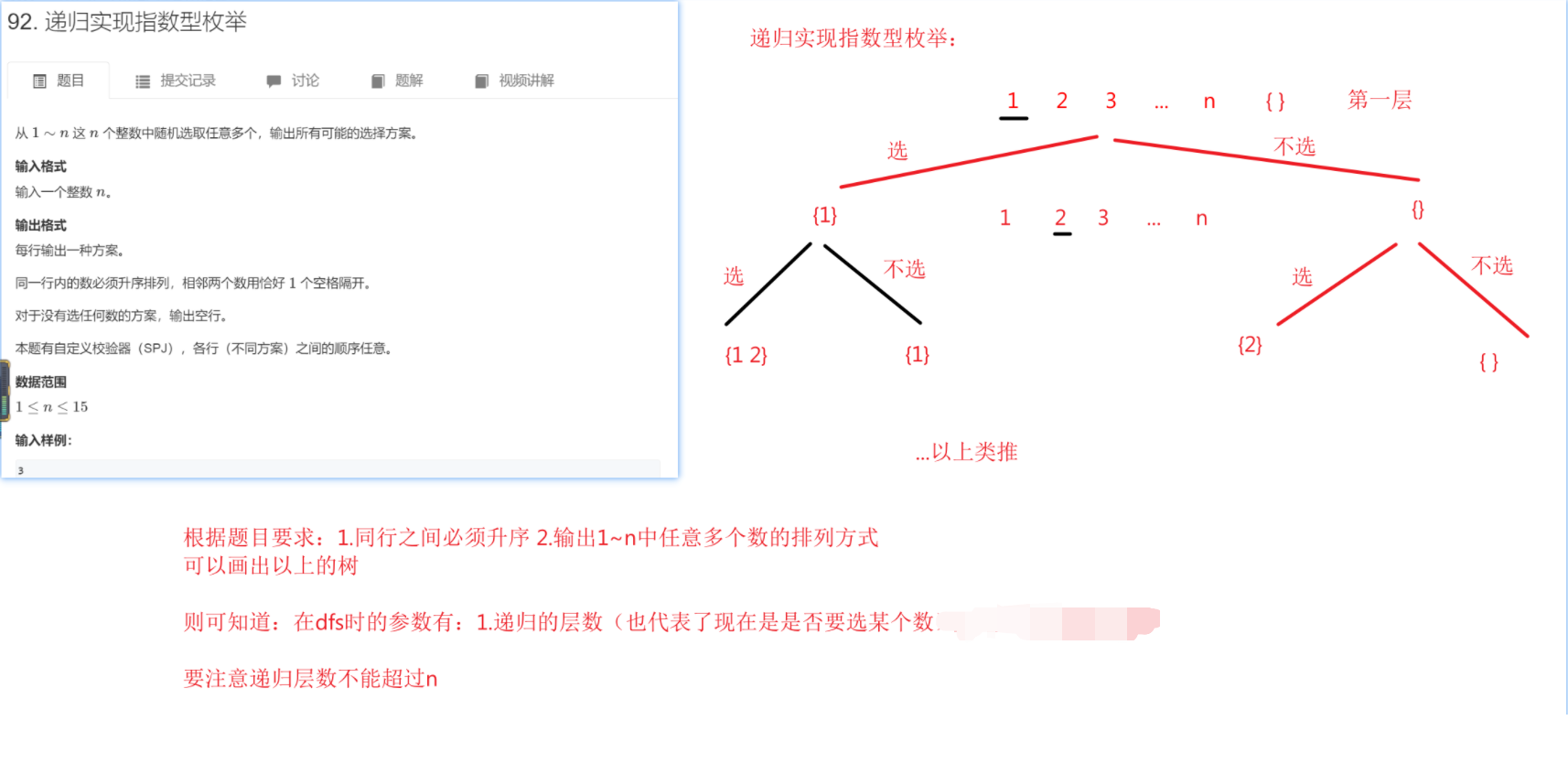
 1 #include <iostream>
 2 #include <cstring>
 3 #include <algorithm>
 4 using namespace std;
 5 const int N = 16;
 6 int n;
 7 bool st[N];
 8 void dfs(int cnt)
 9 {
10     if (cnt > n)
11     {
12         for (int i = 1; i <= n; i++)
13             if (st[i])
14                 cout << i << " ";
15         cout << endl;
16         return ;
17     }
18     st[cnt] = true;
19     dfs(cnt + 1);
20     st[cnt] = false;
21     dfs(cnt + 1);
22 }
23 int main()
24 {
25     cin >> n;
26     dfs(1);
27     return 0;
28 }

《递归实现组合型枚举》

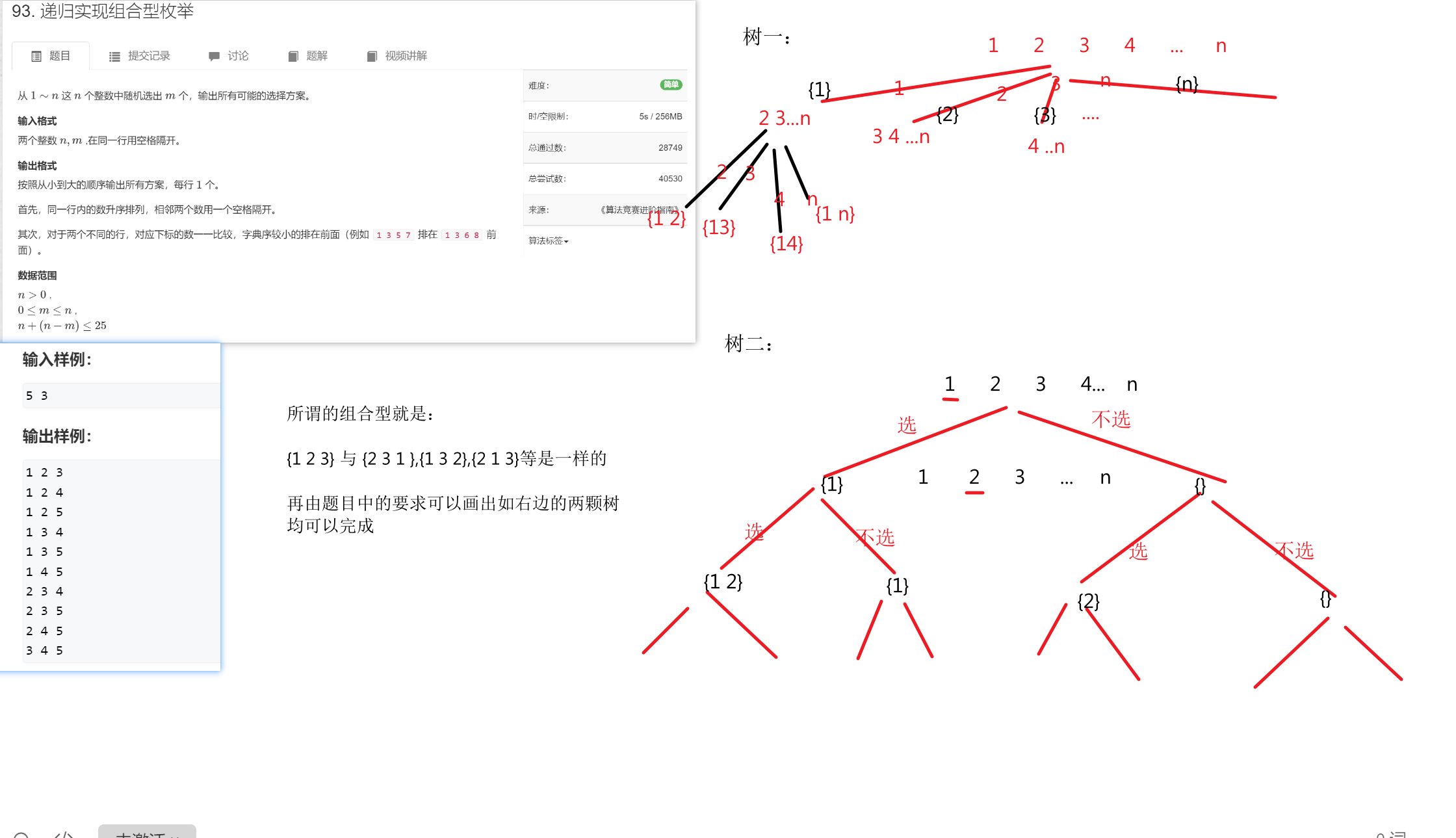
 树二代码：
1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 using namespace std;
 5 const int N = 25;
 6 int n, m;
 7 bool st[N];
 8 void dfs(int u, int cnt)//u表示层数，cnt表示现在集合中元素的个数
 9 {
10     if (u>=n+1 && cnt < m) return ;//注意这里要处理一下边界条件
11     if (cnt >= m)
12     {
13         for (int i = 1; i <= n; i++)
14             if (st[i])
15                 cout << i << " ";
16         cout << endl;
17         return;
18     }
19     st[u] = true;
20     dfs(u + 1, cnt + 1);
21     st[u] = false;
22     dfs(u + 1, cnt);
23 }
24 
25 int main()
26 {
27     cin >> n >> m;
28     dfs(1, 0);
29     return 0;
30 }

中 树一代码：
1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 using namespace std;
 5 const int N = 25;
 6 int n, m;
 7 int path[N];
 8 void dfs(int u, int start)//u表示层数（层数也代表了现在集合的元素个数），start表示现在分支的从那个数开始枚举
 9 {
10     if (u > m)
11     {
12         for (int i = 1; i <= m; i++)
13         {
14             cout << path[i] << " ";
15         }
16         cout << endl;
17         return;
18     }
19     for (int i=start;i<=n;i++)
20     {
21         path[u]=i;
22         dfs(u+1,i+1);
23     }
24 }
25 
26 int main()
27 {
28     cin >> n >> m;
29     dfs(1, 1);
30     return 0;
31 }

《递归实现排列型枚举》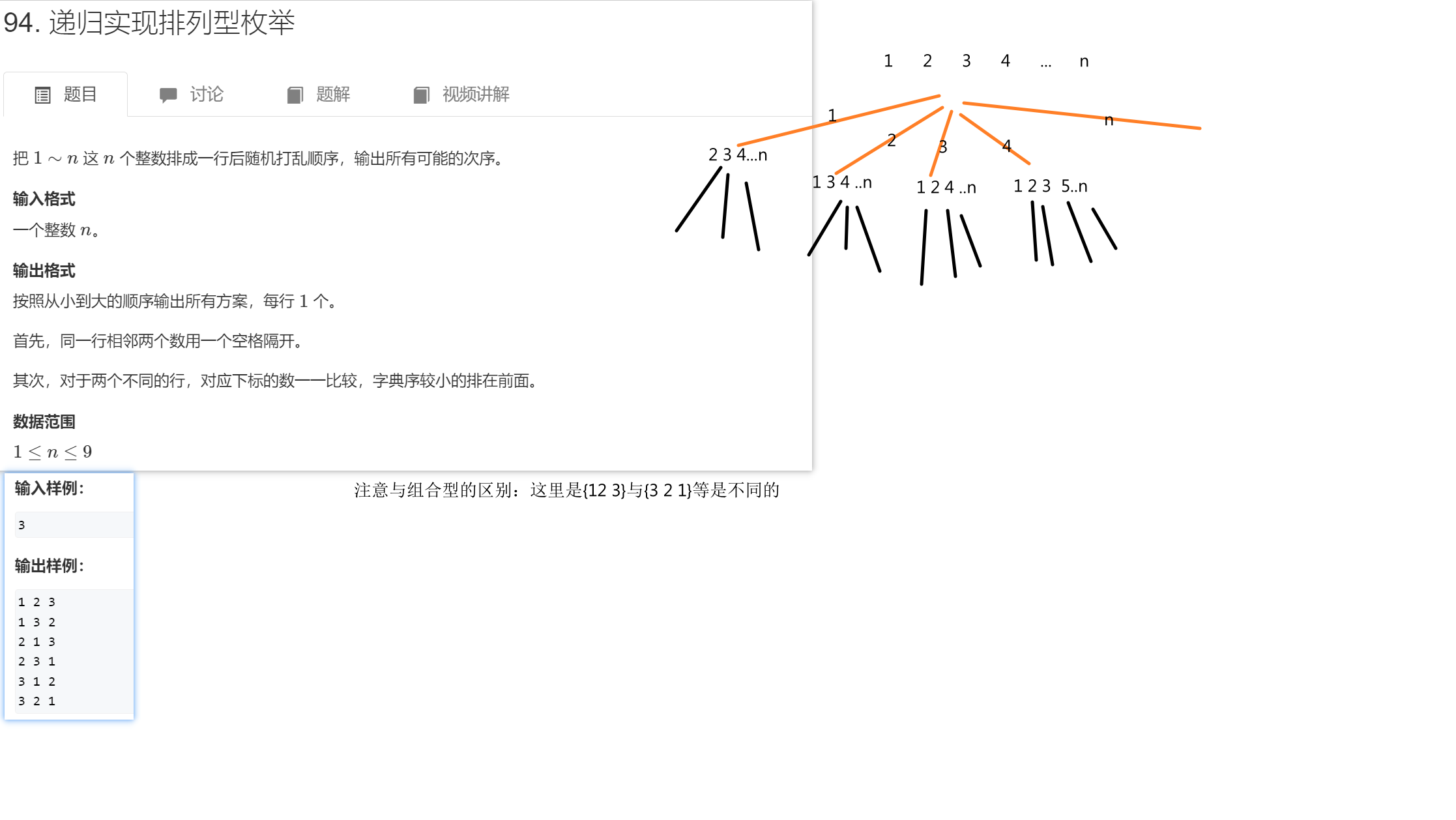

 1 #include <iostream>
 2 #include <cstring>
 3 #include <algorithm>
 4 using namespace std;
 5 const int N = 10;
 6 int n, path[N];
 7 bool st[N];
 8 void dfs(int u)
 9 {
10     if (u>n){
11         for (int i=1;i<=n;i++)
12         {
13             cout<<path[i]<<" ";
14         }
15         cout<<endl;
16         return ;
17     }
18     for (int i=1;i<=n;i++)
19     {
20         if (!st[i]){
21             st[i]=true;
22             path[u]=i;
23             dfs(u+1);
24             st[i]=false;
25         }
26     }
27 }
28 int main()
29 {
30     cin >> n;
31     dfs(1);
32     return 0;
33 }

《分成互质组》

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 using namespace std;
 5 const int N = 12;
 6 int g[N][N], n, nums[N];
 7 bool st[N], ifPrime[N][N];
 8 int ans;
 9 int gcd(int a, int b)
10 {
11     return b ? gcd(b, a % b) : a;
12 }
13 bool check(int a, int gg[], int c)
14 {
15     for (int i = 0; i < c; i++)
16     {
17         if (!ifPrime[a][gg[i]])
18             return false;
19     }
20     return true;
21 }
22 void dfs(int index, int u, int c, int sum)
23 {
24     if (u >= ans)//剪枝
25         return;
26     if (sum >= n)
27         ans = u;
28     bool flag = true;//这一次dfs的决策要不就是添加到最后一组，要不就是开个新组。这里flag是判断要不要开新组
29     for (int i = index; i <= n; i++)
30     {
31         if (!st[i] && check(i, g[u], c))
32         {
33             flag = false;//能进这里就说明有元素可以添加到最后一组,也就是不用开新组
34 
35             st[i] = true;
36             g[u][c] = i;
37             dfs(i + 1, u, c + 1, sum + 1);
38             st[i] = false;
39         }
40     }
41     if (flag)
42         dfs(1, u + 1, 0, sum); //每一次新开一个组就要刷新一下，组内元素各数以及都是从1下标重新开始遍历数了；
43 }
44 int main()
45 {
46     cin >> n;
47     ans = n;
48     for (int i = 1; i <= n; i++)
49         cin >> nums[i];
50     for (int i = 1; i <= n; i++)
51     {
52         for (int j = 1; j <= n; j++)
53         {
54             if (gcd(nums[i], nums[j]) <= 1)
55                 ifPrime[i][j] = ifPrime[j][i] = true;
56             else
57                 ifPrime[i][j] = ifPrime[j][i] = false;
58         }
59     }
60     //现在搜索到的是下标为...，现在搜到的是第...组，现在这个组的下标是...
61     //现在总共搜索了...个数
62     dfs(1, 1, 0, 0);
63     cout<<ans;
64     return 0;
65 }

《dfs的剪枝优化》

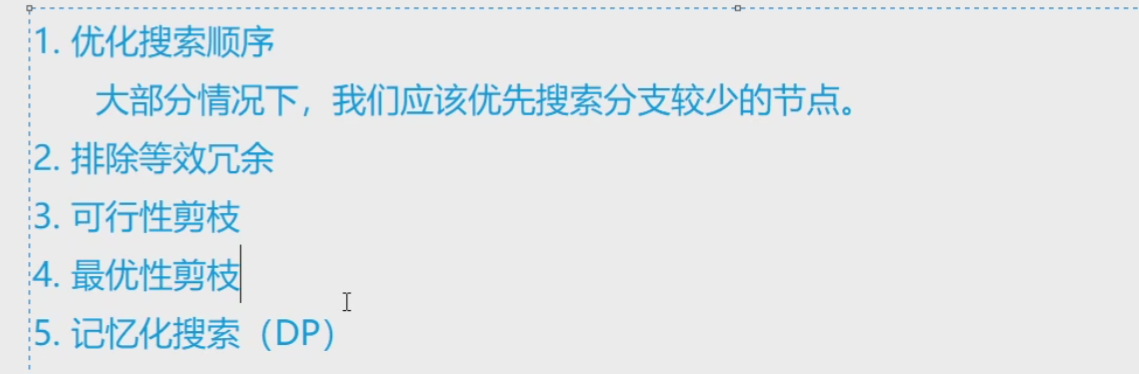
《小猫爬山》

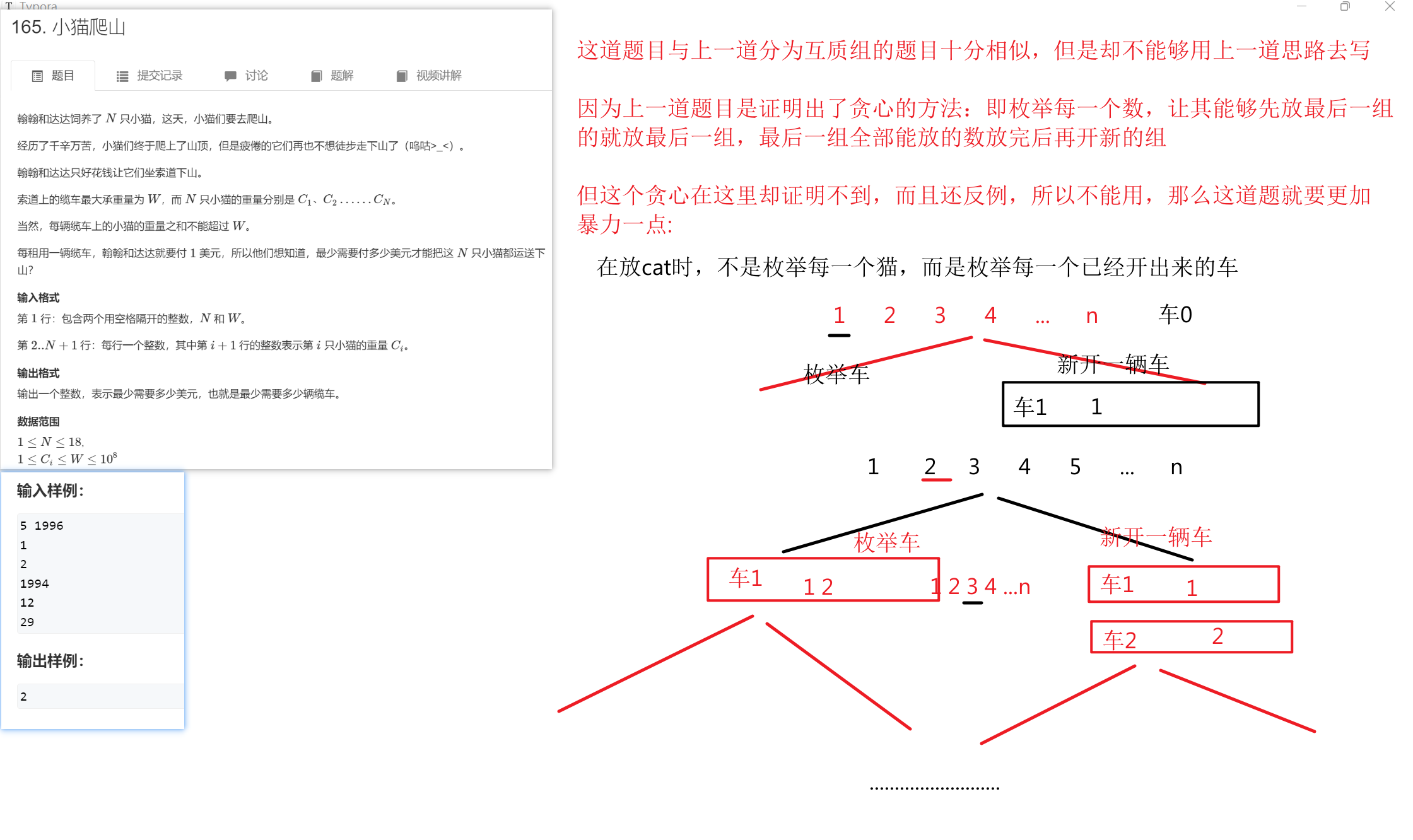
 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 using namespace std;
 5 const int N = 20;
 6 int n, w;
 7 int g[N], cars[N], cnt;
 8 int ans;
 9 bool rule(int a, int b)
10 {
11     return a > b;
12 }
13 void dfs(int u, int k)//第一个参数是现在开了第...个车，第二个参数是先枚举到了第...层（第...个猫）
14 {
15     if (u >= ans)//最优化剪枝
16         return;
17     if (k > n)
18     {
19         ans = u;
20         return;
21     }
22     for (int i = 1; i <= u; i++)
23     {
24         if (cars[i] + g[k] <= w)//可行性剪枝
25         {
26             cars[i] += g[k];
27             dfs(u, k + 1);
28             cars[i] -= g[k];
29         }
30     }
31     cars[u + 1] = g[k];
32     dfs(u + 1, k + 1);
33     cars[u + 1] = 0;
34 }
35 int main()
36 {
37     cin >> n >> w;
38     ans = n;
39     for (int i = 1; i <= n; i++)
40         cin >> g[i];
41     sort(g + 1, g + n + 1, rule);//优化搜索顺序（从最大的猫开始枚举可以大大减少分支）
42     dfs(1, 1);//同时我这里用了组合型递归,减少了冗余项
43     cout << ans;
44     return 0;
45 }

《思考方式》

 1 166. 数独
 2

 3 数独是一种传统益智游戏，你需要把一个 9×9 的数独补充完整，使得数独中每行、每列、每个 3×3 的九宫格内数字 1∼9 均恰好出现一次。
 4 
 5 请编写一个程序填写数独。
 6 
 7 输入格式
 8 输入包含多组测试用例。
 9 
10 每个测试用例占一行，包含 81 个字符，代表数独的 81 个格内数据（顺序总体由上到下，同行由左到右）。
11 
12 每个字符都是一个数字（1−9）或一个 .（表示尚未填充）。
13 
14 您可以假设输入中的每个谜题都只有一个解决方案。
15 
16 文件结尾处为包含单词 end 的单行，表示输入结束。
17 
18 输出格式
19 每个测试用例，输出一行数据，代表填充完全后的数独。
20 
21 输入样例：
22 4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......
23 ......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
24 end
25 输出样例：
26 417369825632158947958724316825437169791586432346912758289643571573291684164875293
27 416837529982465371735129468571298643293746185864351297647913852359682714128574936

即lowbit(20)=在二进制下为100=十进制下2

dfs时，每次找出最小的可枚举的数的格子，每次只用最多枚举81次不用担心

  1 #include <iostream>
  2 #include <cstring>
  3 #include <algorithm>
  4 using namespace std;
  5 const int N = 10;
  6 int row[N], col[N], cell[3][3]; //表示每一行，每一列，每一个九宫格的二进制状态
  7 string str;
  8 // map[]是用来记录如(100)2说明map【i】是1<<几位到了i(打表记录用的);
  9 // ones[]用来记录i一共有ones[i]个1；
 10 int map[1<<10]//注意这里map的大小，不要想当然地写N, ones[N];
 11 void init()
 12 {
　　　　//一开始都是可以用的数，所以都初始化为1

 13     for (int i = 0; i < 9; i++)
 14         row[i] = col[i] = (1 << 9) - 1;
 15     for (int i = 0; i < 3; i++)
 16         for (int j = 0; j < 3; j++)
 17             cell[i][j] = (1 << 9) - 1;
 18 }
 19 int lowbit(int x)
 20 {
 21     return x & -x;
 22 }
 23 bool dfs(int cnt)
 24 {
 25     if (!cnt)
 26         return true;
 27     /* cout << str << endl; */
 28     int minv = 10, y, x, thisState;
 29     int state;
 30     for (int i = 0; i < 9; i++)
 31     {
 32         for (int j = 0; j < 9; j++)
 33         {
 34             if (str[i * 9 + j] == '.')
 35             {
 36                 //获取能够使用的数在二进制下的状态：
 37                 state = row[i] & col[j] & cell[i / 3][j / 3];
 38                 int nowv = ones[state];
 39                 if (minv > nowv)
 40                 {
 41                     minv = nowv;
 42                     y = i, x = j;
 43                     thisState = state;
 44                 }
 45             }
 46         }
 47     }
 48     for (int i = thisState; i; i -= lowbit(i))
 49     {
 50         int num = (1 << map[lowbit(i)]);
 51         row[y] -= num;
 52         col[x] -= num;
 53         cell[y / 3][x / 3] -= num;
 54         str[y * 9 + x] = '1' + map[lowbit(i)];
 55         /* cout << str[y * 9 + x] << " " << map[lowbit(i)] << endl; */
 56         if (dfs(cnt - 1))
 57             return true;
 58         row[y] += num;
 59         col[x] += num;
 60         cell[y / 3][x / 3] += num;
 61         str[y * 9 + x] = '.';
 62     }
 63     return false;
 64 }
 65 int main()
 66 {
 67     for (int i = 0; i < 9; i++)
 68         map[1 << i] = i;
 69    /*  for (int i = 0; i < 9; i++)
 70     {
 71         cout << (1 << i) << " " << map[1 << i] << " "<<endl;
 72     } */
 73    /*  cout << endl; */
 74     /*
 75     如何枚举二进制中0~1<<N的全部数？
 76     其实很简单就是
 77     for (int i=0;i<(1<<N);i++){}
 78     */
 79     memset(ones, 0, sizeof(ones));
 80     for (int i = 0; i < (1 << 9); i++)
 81         for (int j = i; j; j -= lowbit(j))
 82             ones[i]++;
 83     /*  for (int i=0;i<9;i++) cout<<ones[i];
 84      cout<<endl; */
 85     while (cin >> str, str[0] != 'e')
 86     {
 87         //初始化
 88         init();
 89         //根据输入改变二进制的状态
 90         int cnt = 0;
 91         for (int k = 0; k < str.length(); k++)
 92         {
 93             if (str[k] != '.')
 94             {
 95                 int y = k / 9, x = k % 9;
 96                 int num = (1 << (str[k] - '1'));
 97                 row[y] -= num;
 98                 col[x] -= num;
 99                 cell[y / 3][x / 3] -= num;
100             }
101             else
102                 cnt++;
103         }
104         /*  for (int i=0;i<9;i++)
105          {
106              cout<<row[i]<<" ";
107          }
108          cout<<"<-row"<<endl;
109           for (int i=0;i<9;i++)
110          {
111              cout<<col[i]<<" ";
112          }
113           cout<<"<-col"<<endl; */
114         dfs(cnt);
115         cout << str << endl;
116     }
117     return 0;
118 }

《迭代加深》

迭代加深十分适用于dfs时，答案在深度比较浅的地方，但是由于dfs的特性，总是先往深处搜索，导致超时

 1 170. 加成序列
 2 
 3 满足如下条件的序列 X（序列中元素被标号为 1、2、3…m）被称为“加成序列”：
 4 
 5 X[1]=1
 6 X[m]=n
 7 X[1]<X[2]<…<X[m−1]<X[m]
 8 对于每个 k（2≤k≤m）都存在两个整数 i 和 j （1≤i,j≤k−1，i 和 j 可相等），使得 X[k]=X[i]+X[j]。
 9 你的任务是：给定一个整数 n，找出符合上述条件的长度 m 最小的“加成序列”。
10 
11 如果有多个满足要求的答案，只需要找出任意一个可行解。
12 
13 输入格式
14 输入包含多组测试用例。
15 
16 每组测试用例占据一行，包含一个整数 n。
17 
18 当输入为单行的 0 时，表示输入结束。
19 
20 输出格式
21 对于每个测试用例，输出一个满足需求的整数序列，数字之间用空格隔开。
22 
23 每个输出占一行。
24 
25 数据范围
26 1≤n≤100
27 输入样例：
28 5
29 7
30 12
31 15
32 77
33 0
34 输出样例：
35 1 2 4 5
36 1 2 4 6 7
37 1 2 4 8 12
38 1 2 4 5 10 15
39 1 2 4 8 9 17 34 68 77

首先，答案在比较浅的地方是从

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 using namespace std;
 5 const int N = 110;
 6 int n, path[N];
 7 bool dfs(int u, int depth)//当前要枚举的层数是u，规定的深度变量时depth
 8 {
 9     if (u > depth)
10         return false;
11     if (path[u-1] == n)//如果上面一层已经达成目的，返回
12         return true;
13     bool st[N] = {0};
14     for (int i = u-1; i >= 1; i--)
15         for (int j = i; j >= 1; j--)
16         {
17             int sum = path[i] + path[j];
18             if (st[sum] || sum <= path[u - 1] || sum > n)
19                 continue;
20             else
21             {
22                 st[sum] = true;
23                 path[u] = sum;
24                 if (dfs(u + 1, depth))
25                     return true;
26             }
27         }
28     return false;
29 }
30 int main()
31 {
32     path[1] = 1;
33     while (cin >> n, n)
34     {
35         int depth = 2;
36 
37         while (!dfs(2, depth))
38             depth++;
39 
40         for (int i = 1; i < depth; i++)
41             cout << path[i] << " ";
42         cout << endl;
43     }
44     return 0;
45 }

《双向dfs》

https://www.acwing.com/solution/content/38250/

这个博客写的很好

 1 171. 送礼物
 2 达达帮翰翰给女生送礼物，翰翰一共准备了 N 个礼物，其中第 i 个礼物的重量是 G[i]。
 3 
 4 达达的力气很大，他一次可以搬动重量之和不超过 W 的任意多个物品。
 5 
 6 达达希望一次搬掉尽量重的一些物品，请你告诉达达在他的力气范围内一次性能搬动的最大重量是多少。
 7 
 8 输入格式
 9 第一行两个整数，分别代表 W 和 N。
10 
11 以后 N 行，每行一个正整数表示 G[i]。
12 
13 输出格式
14 仅一个整数，表示达达在他的力气范围内一次性能搬动的最大重量。
15 
16 数据范围
17 1≤N≤46,
18 1≤W,G[i]≤231−1
19 输入样例：
20 20 5
21 7
22 5
23 4
24 18
25 1
26 输出样例：
27 19

这个题目dp的话N*W=O(46*(2^32-1))明显超时

普通dfs的话，枚举方式就是对于每一层，这个物品选不选，为2^46超时（2^20约等于1e6）

如果双向dfs一半一半的话：2^23，可以

《dfs时间复杂度分析》

《二维双向dfs》

原题链接:https://atcoder.jp/contests/abc271/tasks/abc271_f

原题题解:https://atcoder.jp/contests/abc271/editorial/4941

原题变形:https://blog.csdn.net/qq_40160605/article/details/81077000?spm=1001.2101.3001.6650.2&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-81077000-blog-124172470.pc_relevant_multi_platform_whitelistv3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2-81077000-blog-124172470.pc_relevant_multi_platform_whitelistv3&utm_relevant_index=3

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 #include <map>
 5 using namespace std;
 6 typedef long long ll;
 7 const int N = 21;
 8 ll g[N][N];
 9 int n;
10 ll ans = 0;
11 map<ll, ll> mapp[N][N];
12 void dfs(int x, int y, ll num)
13 {
14     if (x + y >= n + 1)
15     {
16         mapp[x][y][num]++;
17         return;
18     }
19     if (x + 1 <= n)
20         dfs(x + 1, y, num ^ g[x + 1][y]);
21     if (y + 1 <= n)
22         dfs(x, y + 1, num ^ g[x][y + 1]);
23 }
24 void dfs2(int x, int y, ll num)
25 {
26     if (x + y <= n + 1)
27     {
28         ans += mapp[x][y][num];
29         return;
30     }
31     num ^= g[x][y];
32     if (x - 1 >= 1)
33         dfs2(x - 1, y, num);
34     if (y - 1 >= 1)
35         dfs2(x, y - 1, num);
36 }
37 int main()
38 {
39     cin >> n;
40     for (int i = 1; i <= n; i++)
41         for (int j = 1; j <= n; j++)
42             scanf("%lld", &g[i][j]);
43     dfs(1, 1, 0 ^ g[1][1]);
44     dfs2(n, n, 0);
45     cout << ans;
46     return 0;
47 }

posted @ 2022-07-11 23:15 次林梦叶阅读(49) 评论(0) 收藏举报

刷新页面返回顶部

次林梦叶的小屋

音无结弦之时

Dfs