单源最短路建图问题
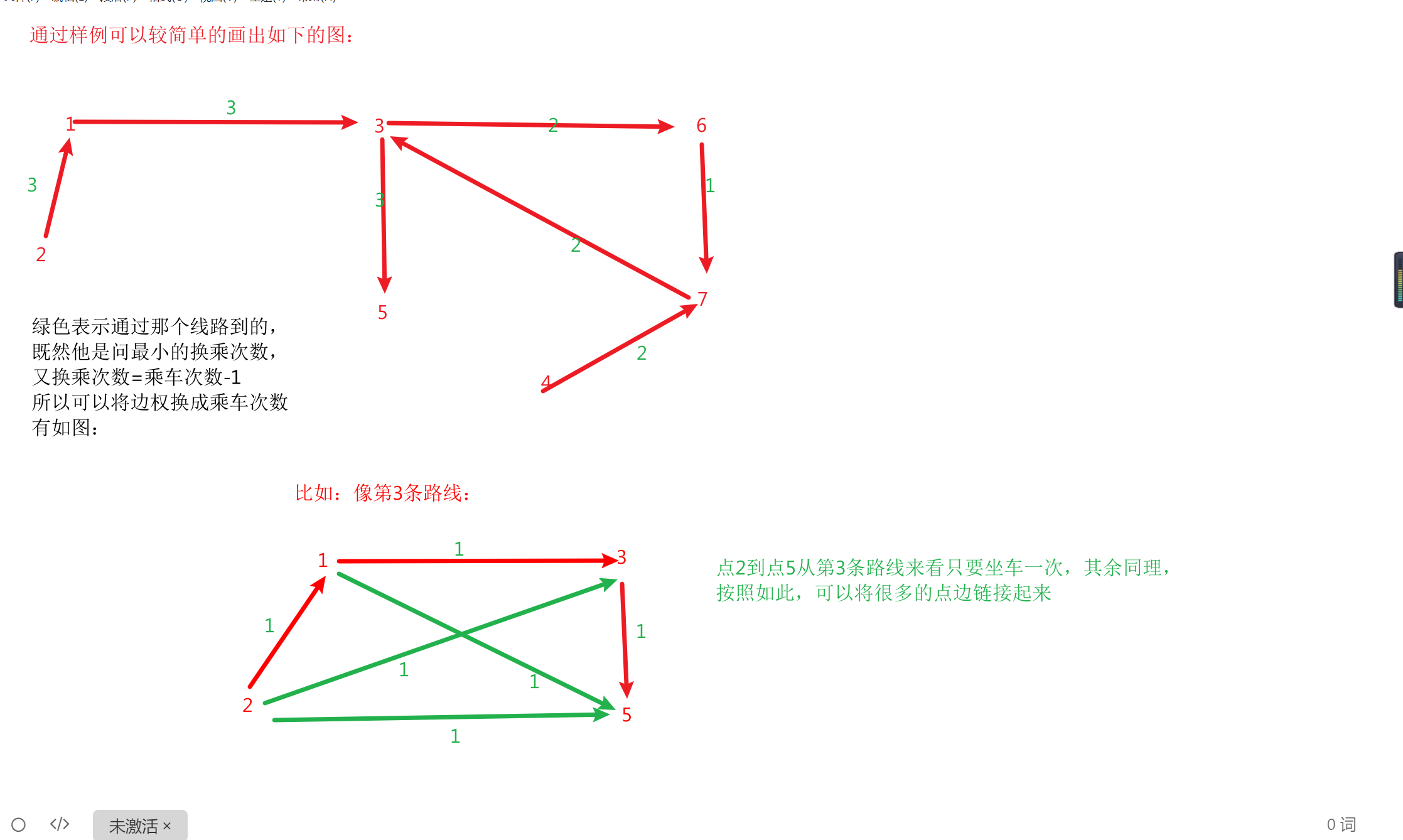
《问题一:通过边权的转化自动建立起图的结构》
1 920. 最优乘车
2
3 H 城是一个旅游胜地,每年都有成千上万的人前来观光。
4
5 为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴士线路。
6
7 每条单程巴士线路从某个巴士站出发,依次途经若干个巴士站,最终到达终点巴士站。
8
9 一名旅客最近到 H 城旅游,他很想去 S 公园游玩,但如果从他所在的饭店没有一路巴士可以直接到达 S 公园,则他可能要先乘某一路巴士坐几站,再下来换乘同一站台的另一路巴士,这样换乘几次后到达 S 公园。
10
11 现在用整数 1,2,…N 给 H 城的所有的巴士站编号,约定这名旅客所在饭店的巴士站编号为 1,S 公园巴士站的编号为 N。
12
13 写一个程序,帮助这名旅客寻找一个最优乘车方案,使他在从饭店乘车到 S 公园的过程中换乘的次数最少。
14
15 输入格式
16 第一行有两个数字 M 和 N,表示开通了 M 条单程巴士线路,总共有 N 个车站。
17
18 从第二行到第 M+1 行依次给出了第 1 条到第 M 条巴士线路的信息,其中第 i+1 行给出的是第 i 条巴士线路的信息,从左至右按运行顺序依次给出了该线路上的所有站号,相邻两个站号之间用一个空格隔开。
19
20 输出格式
21 共一行,如果无法乘巴士从饭店到达 S 公园,则输出 NO,否则输出最少换乘次数,换乘次数为 0 表示不需换车即可到达。
22
23 数据范围
24 1≤M≤100,
25 2≤N≤500
26 输入样例:
27 3 7
28 6 7
29 4 7 3 6
30 2 1 3 5
31 输出样例:
32 2
1 #include <iostream> 2 #include <algorithm> 3 #include <cstring> 4 #include <sstream> 5 using namespace std; 6 const int N = 510, INF = 0x3f3f3f3f; 7 int g[N][N]; //图 8 int dist[N]; 9 bool st[N]; 10 int stop[N]; //表示一条线路上的站点 11 int m, n; 12 void Dijkstra() 13 { 14 memset(dist, 0x3f, sizeof(dist)); 15 for (int i = 1; i <= n; i++) 16 dist[i] = g[1][i]; 17 cout << endl; 18 st[1] = true; 19 for (int i = 1; i <= n; i++) 20 { 21 int v, mindist = INF; 22 for (int j = 1; j <= n; j++) 23 { 24 if (!st[j] && mindist > dist[j]) 25 { 26 v = j; 27 mindist = dist[j]; 28 } 29 } 30 st[v] = true; 31 for (int j = 1; j <= n; j++) 32 { 33 if (!st[j] && dist[j] > dist[v] + g[v][j]) 34 { 35 dist[j] = dist[v] + g[v][j]; 36 } 37 } 38 } 39 } 40 int main() 41 { 42 memset(g, 0x3f, sizeof(g)); 43 for (int i = 1; i <= n; i++) 44 g[i][i] = 0; 45 cin >> m >> n; 46 string str; 47 getline(cin, str); 48 while (m--) 49 { 50 getline(cin, str); 51 stringstream ssin(str); 52 int cnt = 1, p; 53 while (ssin >> p) 54 stop[cnt++] = p; 55 for (int i = 1; i < cnt; i++) 56 { 57 for (int j = i + 1; j < cnt; j++) 58 { 59 g[stop[i]][stop[j]] = 1; 60 } 61 } 62 } 63 Dijkstra(); 64 if (dist[n] >= INF / 2) 65 cout << "NO"; 66 else 67 cout << max(0, dist[n] - 1); 68 return 0; 69 }
上面的输入有点东西:
因为在输入时我不知道他到底有几个点,所以要一行全部读取
memset(g, 0x3f, sizeof(g)); 43 for (int i = 1; i <= n; i++) 44 g[i][i] = 0; 45 cin >> m >> n; 46 string str; 47 getline(cin, str);//这一行是为了读取掉换行符 48 while (m--) 49 { 50 getline(cin, str);//读取一行数据 51 stringstream ssin(str);//将这行数据交给ssin,其按空行分开 52 int cnt = 1, p; 53 while (ssin >> p)//在一次一次将数据交给p 54 stop[cnt++] = p;
《问题二:有附加条件的建图与运用虚拟源点》
1 903. 昂贵的聘礼
8 年轻的探险家来到了一个印第安部落里。
9
10 在那里他和酋长的女儿相爱了,于是便向酋长去求亲。
11
12 酋长要他用 10000 个金币作为聘礼才答应把女儿嫁给他。
13
14 探险家拿不出这么多金币,便请求酋长降低要求。
15
16 酋长说:”嗯,如果你能够替我弄到大祭司的皮袄,我可以只要 8000 金币。如果你能够弄来他的水晶球,那么只要 5000 金币就行了。”
17
18 探险家就跑到大祭司那里,向他要求皮袄或水晶球,大祭司要他用金币来换,或者替他弄来其他的东西,他可以降低价格。
19
20 探险家于是又跑到其他地方,其他人也提出了类似的要求,或者直接用金币换,或者找到其他东西就可以降低价格。
21
22 不过探险家没必要用多样东西去换一样东西,因为不会得到更低的价格。
23
24 探险家现在很需要你的帮忙,让他用最少的金币娶到自己的心上人。
25
26 另外他要告诉你的是,在这个部落里,等级观念十分森严。
27
28 地位差距超过一定限制的两个人之间不会进行任何形式的直接接触,包括交易。
29
30 他是一个外来人,所以可以不受这些限制。
31
32 但是如果他和某个地位较低的人进行了交易,地位较高的的人不会再和他交易,他们认为这样等于是间接接触,反过来也一样。
33
34 因此你需要在考虑所有的情况以后给他提供一个最好的方案。
35
36 为了方便起见,我们把所有的物品从 1 开始进行编号,酋长的允诺也看作一个物品,并且编号总是 1。
37
38 每个物品都有对应的价格 P,主人的地位等级 L,以及一系列的替代品 Ti 和该替代品所对应的”优惠” Vi。
39
40 如果两人地位等级差距超过了 M,就不能”间接交易”。
41
42 你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。
43
44 输入格式
45 输入第一行是两个整数 M,N,依次表示地位等级差距限制和物品的总数。
46
47 接下来按照编号从小到大依次给出了 N 个物品的描述。
48
49 每个物品的描述开头是三个非负整数 P、L、X,依次表示该物品的价格、主人的地位等级和替代品总数。
50
51 接下来 X 行每行包括两个整数 T 和 V,分别表示替代品的编号和”优惠价格”。
52
53 输出格式
54 输出最少需要的金币数。
55
56 数据范围
57 1≤N≤100,
58 1≤P≤10000,
59 1≤L,M≤N,
60 0≤X<N
61 输入格式
62 1 4
63 10000 3 2
64 2 8000
65 3 5000
66 1000 2 1
67 4 200
68 3000 2 1
69 4 200
70 50 2 0
71 输出格式
72 5250
这里运用虚拟源点我倒是想到了,但是还有等级制度该怎么办?

1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 #include <cmath>
5 using namespace std;
6 const int N = 110, INF = 0x3f3f3f3f;
7 int m, n;
8 int g[N][N], L[N]; // L是用来记录点的地位的;
9 int dist[N];
10 bool st[N];
11 void Dijkstra(int str, int fin)
12 {
13 memset(st, false, sizeof(st));
14 memset(dist, 0x3f, sizeof(dist));
15 for (int i = 1; i <= n; i++)
16 {
17 if (str <= L[i] && fin >= L[i])
18 dist[i] = g[0][i];
19 else
20 dist[i] = INF;
21 }
22 st[0] = true;
23 for (int i = 1; i <= n; i++)
24 {
25 int v, mindist = INF;
26 for (int j = 1; j <= n; j++)
27 {
28 if (!st[j] && mindist > dist[j])
29 {
30 v = j;
31 mindist = dist[j];
32 }
33 }
34 st[v] = true;
35 for (int j = 1; j <= n; j++)
36 {
37 if (!st[j] && dist[j] > dist[v] + g[v][j] &&
38 str <= L[j] && fin >= L[j])
39 {
40 dist[j] = dist[v] + g[v][j];
41 }
42 }
43 }
44 }
45 int main()
46 {
47 memset(g, 0x3f, sizeof(g));
48 cin >> m >> n;
49 int boosl;
50 for (int i = 1; i <= n; i++) //开始枚举物品
51 {
52 int p, l, x;
53 cin >> p >> l >> x;
54 if (i == 1)
55 boosl = l;
56 L[i] = l;
57 g[0][i] = p;
58 for (int j = 1; j <= x; j++) //开始枚举交换的物品
59 {
60 int t, v;
61 cin >> t >> v;
62 g[t][i] = v;
63 }
64 }
65 int ans = INF;
66 for (int i = boosl - m; i <= boosl; i++)
67 {
68 Dijkstra(i, i + m);
69 ans = min(dist[1], ans);
70 }
71 cout << ans;
72 return 0;
73 }
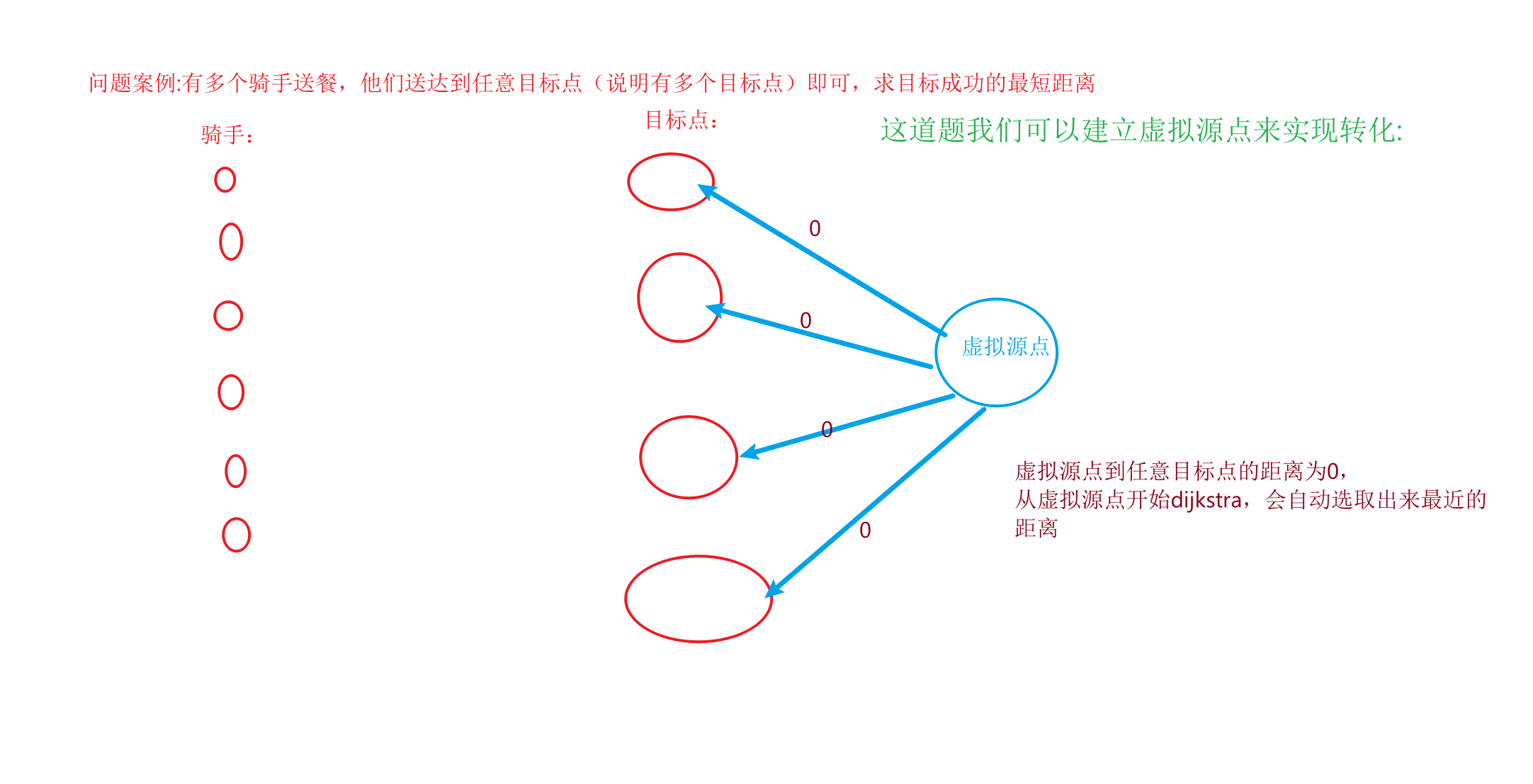
《将从求多个起点到多个目标点的最小距离转化成单元最短路问题》


 浙公网安备 33010602011771号
浙公网安备 33010602011771号