dp----最长上升子序列问题

最原始问题：

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式
第一行包含整数 N。

第二行包含 N 个整数，表示完整序列。

输出格式
输出一个整数，表示最大长度。

数据范围
1≤N≤1000，
−109≤数列中的数≤109
输入样例：
7
3 1 2 1 8 5 6
输出样例：
4

最原始解法：

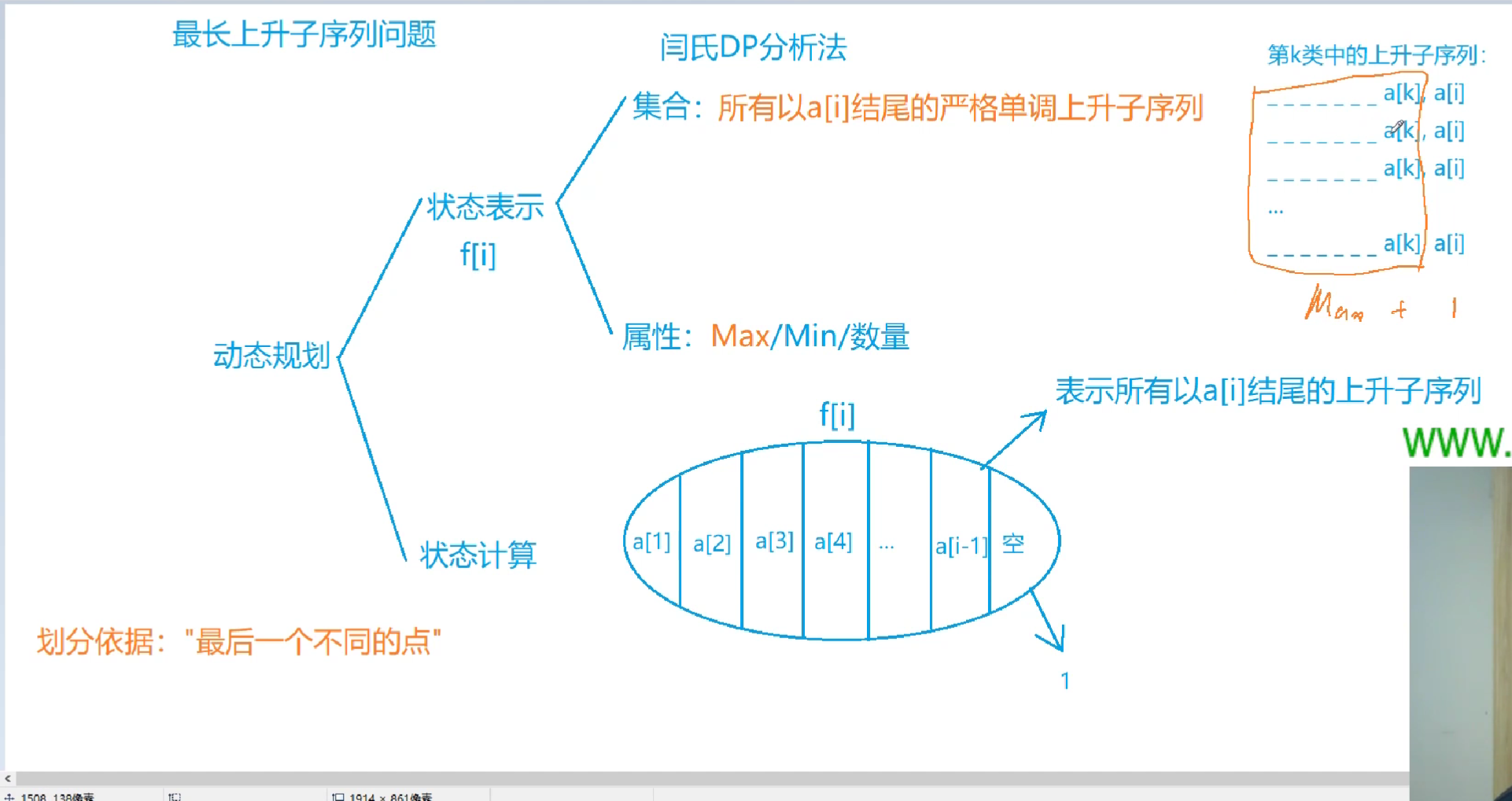
 《变式----最长上升子序列+最长下降子序列》

1014. 登山

五一到了，ACM队组织大家去登山观光，队员们发现山上一共有N个景点，并且决定按照顺序来浏览这些景点，即每次所浏览景点的编号都要大于前一个浏览景点的编号。

同时队员们还有另一个登山习惯，就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了。

队员们希望在满足上面条件的同时，尽可能多的浏览景点，你能帮他们找出最多可能浏览的景点数么？

输入格式
第一行包含整数N，表示景点数量。

第二行包含N个整数，表示每个景点的海拔。

输出格式
输出一个整数，表示最多能浏览的景点数。

数据范围
2≤N≤1000
输入样例：
8
186 186 150 200 160 130 197 220
输出样例：
4
题源：AcWing 1014. 登山

 

 代码：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
int ldp[N], rdp[N], h[N];
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &h[i]);
    }
    for (int i = 1; i <= n; i++)
    {
        ldp[i] = 1;//注意千万不能忘记这一步，因为就算什么都比不上，还有自己这个
        for (int j = 1; j < i; j++)
        {
            if (h[j] < h[i])
            {
                ldp[i] = max(ldp[i], ldp[j] + 1);
            }
        }
    }
    for (int i=n;i>=1;i--)
    {
        for (int j=n;j>=i+1;j--)
        {
            if (h[i]>h[j])
            {
                rdp[i]=max(rdp[i],rdp[j]+1);
            }
        }
        ldp[i]+=rdp[i];
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        ans = max(ldp[i], ans);
    }
    printf("%d", ans);
    return 0;
}

 《最长上升子序列问题----其中的贪心问题》

1010. 拦截导弹
拦截导弹袭击，发展出一种导弹拦截系统。

但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。

某天，雷达捕捉到敌国的导弹来袭。

由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式
共一行，输入导弹依次飞来的高度。

输出格式
第一行包含一个整数，表示最多能拦截的导弹数。

第二行包含一个整数，表示要拦截所有导弹最少要配备的系统数。

数据范围
雷达给出的高度数据是不大于 30000 的正整数，导弹数不超过 1000。

输入样例：
389 207 155 300 299 170 158 65
输出样例：
6
2

主要是第二问：

要拦截所有导弹最少要配备的系统数。

 关于为什么g是一个单调递增的数组，是因为g每次新开一个都是因为现在的导弹高度都大于已有的系统记录高度

#include <iostream>
#include <algorithm>
#include <cstring>
#include <sstream>
using namespace std;
const int N = 1010;
int h[N], dp[N];
int main()
{
    string str;
    getline(cin, str);
    stringstream ssin(str);
    int cnt = 1;
    while (ssin >> h[cnt])
        cnt++;
    cnt--;
    /*  for (int i=1;i<=cnt;i++)
     {
         cout<<h[i]<<" ";
     }
     cout<<endl; */
    int maxNum = 0;
    for (int i = cnt; i >= 1; i--)
    {
        dp[i] = 1;
        for (int j = cnt; j >= i + 1; j--)
        {
            if (h[i] >= h[j])
            {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
        maxNum = max(maxNum, dp[i]);
    }
    cout << maxNum << endl;
    int g[N], cot = 0;
    //g[N]保存的是每一套系统最后拦截的导弹的高度
    //cot是现在系统拥有的个数
    for (int i = 1; i <= cnt; i++)//对于每一个导弹都要拦截，所以枚举每一个导弹
    {
        int k = 1;//每次从第一个系统开始看
        while (k <= cot && h[i] > g[k]) //按我这个思想，能够保证g是一个递增的数组
            k++;//当h[i]<=g[k]时，就是找到了最小的且大于等于h[i]的系统计入数
        g[k] = h[i];//找到了更新一下，没找到则开一个新的系统
        if (k > cot)
            cot++;//系统数更新
    }
    cout<<cot;
    return 0;
}