初学算法----动态规划题目
向四周判断的动态规划:
滑雪
描述:
Michael喜欢滑雪百这并不奇怪, 因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度减小。在上面的例子中,一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上,这是最长的一条。
输入:
输入的第一行表示区域的行数R和列数C(1 <= R,C <= 100)。下面是R行,每行有C个整数,代表高度h,0<=h<=10000。输出:
输出最长区域的长度。样例输入:
5 5 1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9
样例输出:
25
这道题目写出记忆化搜索(递归)形式不难,但递推形式要一点技巧;
#include <bits/stdc++.h>
using namespace std;
int row, line, counter = 1, dp[100000], dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0};//这里dx,dy是写方向的常见写法;
struct E
{
int x;
int y;
int h;
} maper[100000];
bool rule1(E a, E b)
{
return a.h < b.h;
}
bool ifaround(int i, int j)
{
for (int k = 0; k < 4; k++)
{
int rex = maper[i].x + dx[k];
int rey = maper[i].y + dy[k];
if (rex == maper[j].x && rey == maper[j].y)
{
return true;
}
}
return false;
}
int main()
{
//输入数据;
cin >> row >> line;
//将二维数组转化为一维数组,便于递推;
for (int i = 1; i <= row; i++)
{
for (int j = 1; j <= line; j++)
{
dp[counter] = 1;//这里再强调一下memset只能初始化0,-1而不是1;
maper[counter].x = j;
maper[counter].y = i;
cin >> maper[counter].h;
counter++;
}
}
//将数组按高度从小到大排列;
sort(maper + 1, maper + counter, rule1);
//递推dp数组;
for (int i = 1; i < counter; i++)
{
for (int j = i - 1; j >= 1; j--)
{
if (ifaround(i, j) && maper[i].h > maper[j].h )//这里加上maper[i].h > maper[j].h 是为了防止高度重复的情况;
{
//因为有4种走法,要选出最大长度的走法;
dp[i] = max(dp[j] + 1, dp[i]);
}
}
}
int answer = 0;
for (int i = 1; i < counter; i++)
{
answer = max(answer, dp[i]);
}
cout << answer;
return 0;
}
多亏了这位大佬的测试数据让我写出来了:https://blog.csdn.net/huanghanqian/article/details/51646241;
与广度优先搜索十分相像的题目(不是在再求最值,而是问个数):
神奇的口袋
描述:
有一个神奇的口袋,总的容积是40,用这个口袋可以变出一些物品,这些物品的总体积必须是40。John现在有n个想要得到的物品,每个物品的体积分别是a1,a2……an。John可以从这些物品中选择一些,如果选出的物体的总体积是40,那么利用这个神奇的口袋,John就可以得到这些物品。现在的问题是,John有多少种不同的选择物品的方式。输入:
输入的第一行是正整数n (1 <= n <= 20),表示不同的物品的数目。接下来的n行,每行有一个1到40之间的正整数,分别给出a1,a2……an的值。输出:
输出不同的选择物品的方式的数目。样例输入:
3 20 20 20
样例输出3
解法1:广度优先搜索: 我这个dfs写的有点奇葩,一般dfs的函数初始调用是从底部开始而我这里是dfs(n,40)
#include<bits/stdc++.h>
using namespace std;
int itemsv[25],allway=0,n;
//dfs的作用是从前面的k件物品中,挑选出体积是nowallv的各个物品;
void dfs (int k,int nowallv)
{
if (k<0 || nowallv<0)//这里k并不能判断为==0,若k是<=0mowallv
//,那么就会少掉当第一个正好挑出使mowallv==0,而没有让allway++的情况;
{
return ;
}
if (nowallv==0)
{
allway++;
return ;
}
for (int i=k;i>=1;i--)
{
nowallv-=itemsv[i];
dfs(i-1,nowallv);
nowallv+=itemsv[i];//回溯,这个回溯效果会帮助实现在第i个物品时不去拿这个物品;
同时我也不用列个什么for 循环来,要起始点从i=n开始到i=1;回溯可以实现其全部情况,不管是起始从n开始,还是25等开始;
}
}
int main()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>itemsv[i];
}
dfs (n,40);
cout<<allway;
return 0;
}
解法2 : 普通递归
这个是为写递推做准备,会发现递推大多是从最后的情况写起;
#include<bits/stdc++.h>
using namespace std;
int itemsv[45];
//递归的作用是从前面的k件物品中,挑选出体积是nowallv的各个物品;
int recursion (int k,int nowallv)
{
if (nowallv==0)
{
return 1;
}
if (k<0 || nowallv<0)
{
return 0;
}
return recursion(k-1,nowallv)+recursion(k-1,nowallv-itemsv[k]);//这个有点像放苹果的那道 return ;感觉很有灵魂
}
int main()
{
int n;
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>itemsv[i];
}
int allway=recursion (n,40);
cout<<allway;
return 0;
}
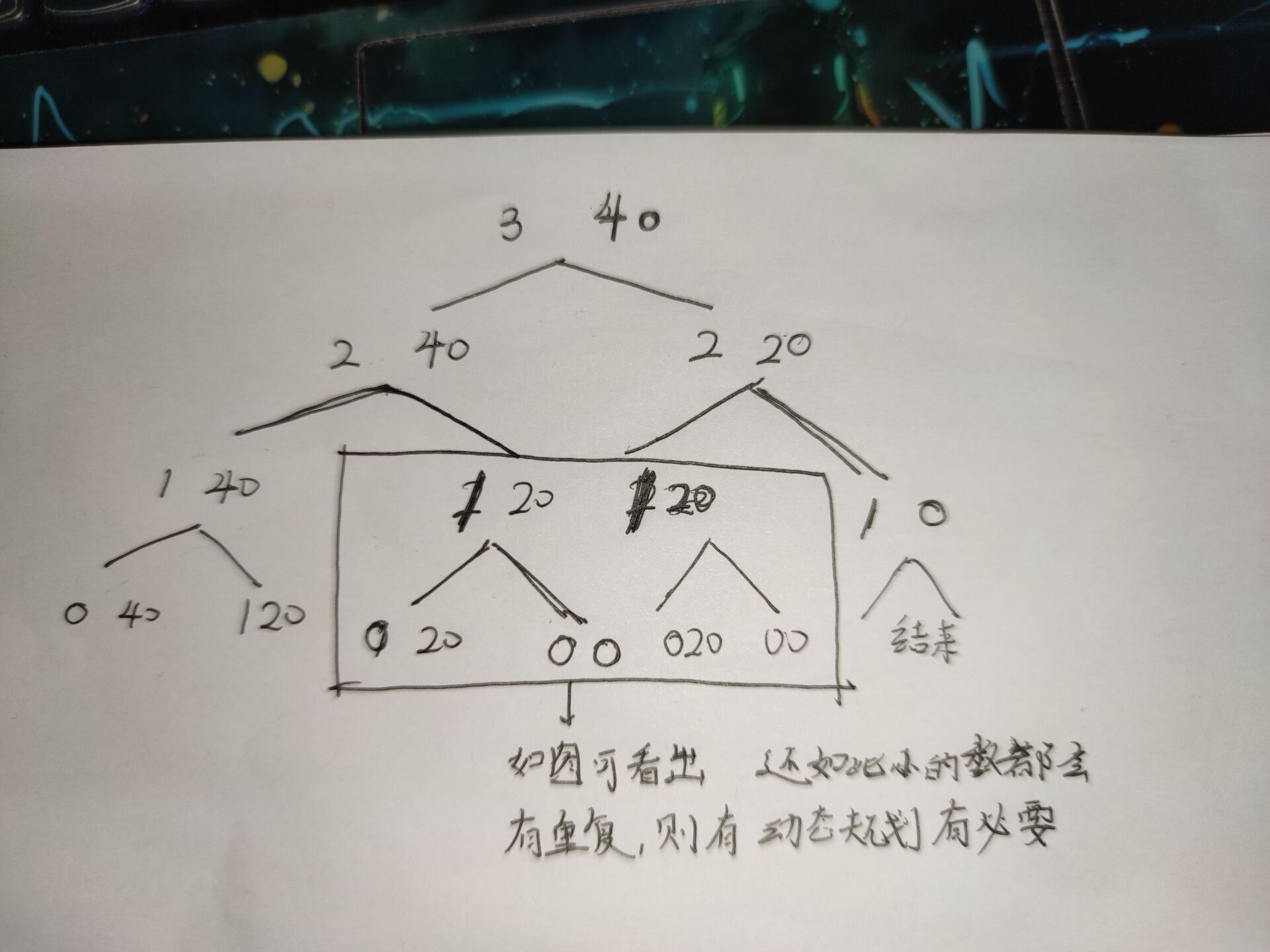
解法3: 动态规划:
#include<bits/stdc++.h>
using namespace std;
int itemsv[25],dp[25][45];
//dp[i][j]数组的作用是记录在前面i件物品中挑选总体积小于j的总方法;
int main()
{
int n;
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>itemsv[i];
}
//初始化边界条件;
memset(dp,0,sizeof(dp));
for (int i=0;i<=n;i++)
{
dp[i][0]=1;//结束条件,让最后剩余体积等于0的都为一种方法;
}
for (int i=1;i<=n;i++)
{
for (int j=1;j<=40;j++)
{
int restv=j-itemsv[i];
if (restv<0)
{
dp[i][j]=dp[i-1][j]+0;
}
else
{
dp[i][j]=dp[i-1][j]+dp[i-1][restv];
}
}
}
cout<<dp[n][40];
return 0;
}
可以提高效率的动态规划:
复杂的整数划分问题
描述:
将正整数n 表示成一系列正整数之和,n=n1+n2+…+nk, 其中n1>=n2>=…>=nk>=1 ,k>=1 。
正整数n 的这种表示称为正整数n 的划分。
输入:
标准的输入包含若干组测试数据。每组测试数据是一行输入数据,包括两个整数N 和 K。(0 < N <= 50, 0 < K <= N)
输出:
对于每组测试数据,输出以下三行数据:第一行: N划分成K个正整数之和的划分数目
第二行: N划分成若干个不同正整数之和的划分数目
第三行: N划分成若干个奇正整数之和的划分数目
样例输入:
5 2
样例输出:
2 3 3
注释:
第一行: 4+1, 3+2,第二行: 5,4+1,3+2
第三行: 5,1+1+3, 1+1+1+1+1+1
这道题可以说完全是一个递归题,但可以用动态规划提高效率;(这道题与放苹果简直异曲同工,我递归菜的难,还是不会以下有大佬的启发)
我的错误代码,下次来改吧:
#include<bits/stdc++.h>
#include<cstring>
using namespace std;
int dp1[60][60],dp2[60][60],dp3[60][60];
//dp1[n][k]的作用是将数字n划分成k个正整数之和的划分数目;
//dp2[n][k]的作用是将数字n划分成若干个不同正整数之和的划分数目,
//其中每个数字大小不超过k
//dp3[n][k]的作用是将数字n划分成若干个奇正整数之和的划分数目,
//其中每个数字大小不超过k
int main()
{
int n,k;
while (cin>>n>>k)
{
//第一行输出:
memset (dp1,0,sizeof (dp1));
for (int i=1;i<=n;i++)
{
dp1[i][i]=1;
dp1[i][1]=1;
}
for (int i=k+1;i<=n;i++)
{
for (int j=2;j<=k;j++)
{
dp1[i][j]=dp1[i-1][j-1]+dp1[i-j][j];
}
}
cout<<dp1[n][k]<<endl;
//第二行输出:
memset(dp2,0,sizeof (dp2));
for (int i=0;i<=n;i++)
//初始化,当k==0时,每个数字大小不超过k,
//则说明是不可能的,全为0;当n==0时,说明其将整个数都划分出去了
//又有dp[i][j]当i<j时dp[i][j]==dp[i][i],则干脆全初始化为1;
{
dp2[0][i]=1;
//dp2[i][1]=1;这条语句是不行的,因为划分成若干个不同正整数之和;
}
for (int i=1;i<=n;i++)
{
for (int j=1;j<=n;j++)
{
if (i<j)
{
dp2[i][j]=dp2[i][i];
}
else
{
dp2[i][j]=dp2[i-j][j-1]+dp2[i][j-1];
}
}
}
cout<<dp2[n][n]<<endl;
//第三行输出:
memset(dp3,0,sizeof (dp3));
for (int i=0;i<=n;i++)
{
dp3[0][i]=1;
dp3[i][1]=1;
}
for (int i=1;i<=n;i++)
{
for (int j=2;j<=n;j++)
{
if (i<j)
{
dp3[i][j]=dp3[i][i];
}
else
{
if (j%2==0)
{
dp3[i][j]=dp3[i][j-1];
}
else
{
dp3[i][j]=dp3[i-j][j]+dp3[i][j-1];
}
}
}
}
cout<<dp3[n][n]<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号