初学算法----分而治之

 

分治算法详解

 

CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接： https://blog.csdn.net/effective_coder/article/details/8697789

这位大佬把分治讲的很明白;

接下来是我内容:

对快速排序的理解:     (翁恺老师的代码)

 选取array[0]为基准-----

i,j两个指针-----

通过(奇数次交换则j向左扫,偶数次交换i向右扫)的规则,-------

会发现总会有一个指针指向基准,--------

这就保证了基准一定可以在正确的位置且,比基准小的在左边,比基准大的在右边.--------

代码如下:

 

#include<iostream>
#include<cstdio>
using namespace std;

void swap (int & a,int & b) //交换函数
{
int temp=a;
a=b;
b=temp;
}

void quicksort (int start,int finall,int array[])
{
int i=start,j=finall;
int key=array[start];
//递归出口条件,当只有一个元素时是绝对有有序的;
if (i>=j)//注意 这里不能写i==j ,还可能出现 i>j的情况,这时可能会发生数组越界
{
return ;
}
//当还有其他元素时:
while (i<j)
{
while (key<=array[j] && i<j) //因为基准为array[start],所以从最右边开始.
{
j--;
}
swap (array[i],array[j]);
while (key>=array[i] && i<j)
{
i++;
}
swap (array[i],array[j]);
}
quicksort (start,i-1,array);//没有i是因为i已经回到了他该去的地方了
quicksort (i+1,finall,array);
}

int main()
{
//获得测试数据
int array[1000]={};
int n;
scanf ("%d",&n);
for (int i=0;i<n;i++)
{
scanf ("%d",&array[i]);
}

//开始进行快速排序
quicksort (0,n-1,array);

//测试代码
for (int i=0;i<n;i++)
{
printf ("%d ",array[i]);
}

return 0;
}

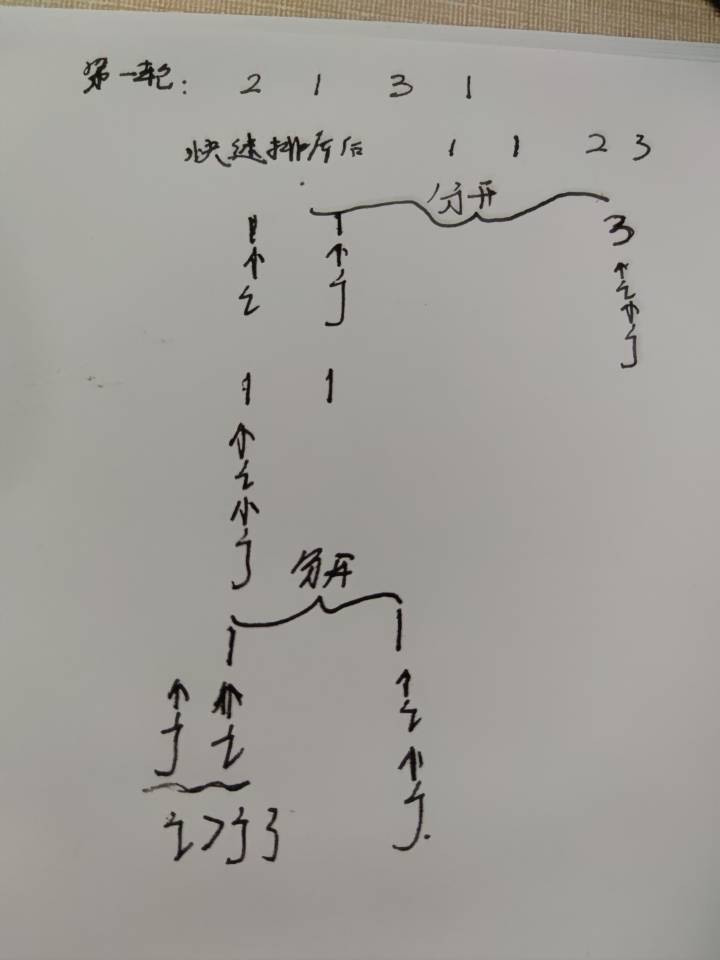
接下来说明一下 i>j的情况:

 //-----------------------------------------------------------------------------------------------

还有归并排序:

基本思想:

让一个数组的各一半的元素有序,然后归并,元素必然有序;

不断分半,直到只剩下一个元素,一个元素必然有序,经过比较,得到有序:

#include<iostream>
#include<cstdio>
using namespace std;
void merge(int data[],int start,int mid,int finall,int savedata[]);

void mergesort(int data[],int start,int finall,int savedata[]);

int main()
{
int data[1000],savedata[1000];
int n;
scanf ("%d",&n);
for (int i=0;i<n;i++)
{
scanf ("%d",&data[i]);
}
mergesort(data,0,n-1,savedata);
for (int i=0;i<n;i++)
{
printf ("%d ",savedata[i]);
}
return 0;
}

void merge(int data[],int start,int mid,int finall,int savedata[])
{
int line1=start;
int line2=mid+1;
int sub=0;
while (line1<=mid && line2<=finall)
{
if (data[line1]<=data[line2])
{
savedata[sub++]=data[line1++];
}
else if(data[line1]>data[line2])
{
savedata[sub++]=data[line2++];
}
}
while (line1<=mid)
{
savedata[sub++]=data[line1++];
}
while (line2<=finall)
{
savedata[sub++]=data[line2++];
}
for (int i=0;i<sub;i++)
{
data[start+i]=savedata[i];
}
}

void mergesort(int data[],int start,int finall,int savedata[])
{
if (start<finall)
{
int mid=start+(finall-start)/2;
mergesort (data,start,mid,savedata);
mergesort (data,mid+1,finall,savedata);
merge(data,start,mid,finall,savedata);
}
}