剑指offer_整数中1出现的次数

方法一

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {
        int sum = 0;
        for(int i=1;i<=n;i++){
           sum+=howmany(i);
        }
        return sum;
    }
    public int howmany(int i){
        int temp=0;
        while(i/10!=0){
            if(i%10==1) temp++;
            i=i/10;
        }
        if(i==1) temp++;
        return temp;
    }
}

方法二

public int NumberOf1Between1AndN_Solution(int n) {
int cnt = 0;
for (int m = 1; m <= n; m *= 10) {
int a = n / m, b = n % m;
cnt += (a + 8) / 10 * m + (a % 10 == 1 ? b + 1 : 0);
}
return cnt;
}

当n = 3141592时

 

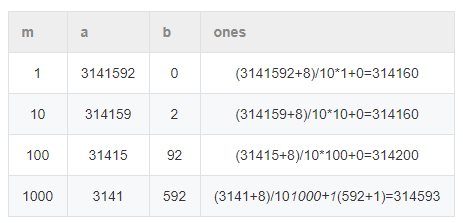
当然后面还有m=10000,100000,1000000三种情况，对应着万位，十万位， 百万位为1时的情况

下面说下a+8的意义：

当考虑个位，十位，百位这三位为1的情况时：

个位 2 ，当个位取值1时，前面的六位数字可由0~314159组成，即314160种情况

十位9，当十位取值1时，前面的五位数字可由0~31415组成，十位之后的一位可由0~9组成，组合情况31416*10=314160种情况

百位5，当百位取值为1时，前面的四位数字可由0~3141组成，百位之后的两位可由0~99组成，组合情况为3142*100=314200种情况

注意：当考虑千位1时：

千位1，千位取值即1，前面的三位数字可由0~314组成，但是当前面的值为314时，后面的三位只有0~592种情况(特殊情况)，其余的情况即为前面的值为0~313,后面三位有0~999,情况数为3141000，所以总情况数为3141000 + 593=314593种情况

这时可发现和代码中的公式算的情况是吻合的，a+8的巧妙之处在于当a的最后一位(当前分析位)为0或1时，加8不产生进位，这是为需要单独算的特殊情况做准备，而当前分析位为2~9时，不需要考虑特殊情况，所以允许加8产生的进位。