剑指offer_ 矩形覆盖

我们可以用 2*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩 形，总共有多少种方法？

解题思路，当n为1时，只有一种覆盖方法，当n为2时有两种覆盖方法

要覆盖 2*n 的大矩形，可以先覆盖 2*1 的矩形，再覆盖 2*(n-1) 的矩形；或者先覆盖 2*2 的矩形，再覆盖 2*(n-2) 的矩形。而覆盖 2*(n-1) 和 2*(n-2) 的矩形可以看成子问题。该问题的递推公式如下：

 

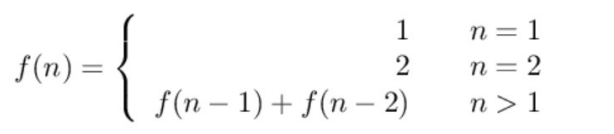
 显而易见，我们可以采用递归或循环

首先是递归

1 public class Solution {
2     public int RectCover(int n) {
3         if(n<=2) return n;
4         return RectCover(n-1)+RectCover(n-2);
5     }
6 }

算法简单但是运算速度和效率慢

再看看循环的方法

 1 public int RectCover(int n) {
 2 if (n <= 2)
 3 return n;
 4 int pre2 = 1, pre1 = 2;
 5 int result = 0;
 6 for (int i = 3; i <= n; i++) {
 7 result = pre2 + pre1;
 8 pre2 = pre1;
 9 pre1 = result;
10 }
11 return result;
12 }

这题主要要想到递推式就很容易解决了

posted @ 2019-08-13 09:05  chyblogs  阅读(95)  评论(0)    收藏  举报