剑指offer_二维数组中的查找

给定一个二维数组，其每一行从左到右递增排序，从上到下也是递增排序。给定一个数，判断这个数是否在该二维数 组中。

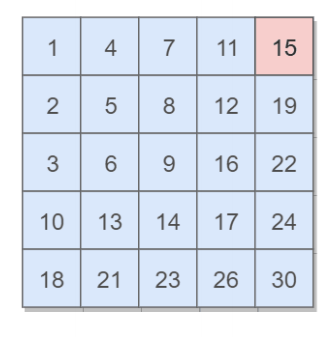
Consider the following matrix:

[

[1, 4, 7, 11, 15],

[2, 5, 8, 12, 19],

[3, 6, 9, 16, 22],

[10, 13, 14, 17, 24],

[18, 21, 23, 26, 30]

]

Given target = 5, return true.

Given target = 20, return false.

首先是司空见惯的暴力法：

public class Solution {
    public boolean Find(int target, int [][] array) {
        for(int i=0;i<array.length;i++){
            for(int j=0; j<array[i].length;j++){
                if(array[i][j]==target) return true;
            }
        }
        return false;
    }
}

暴力法是实在没思路的时候写上去的，实在没有太大意义。

要求时间复杂度 O(M + N)，空间复杂度 O(1)。其中 M 为行数，N 为 列数。 该二维数组中的一个数，小于它的数一定在其左边，大于它的数一定在其下边。因此，从右上角开始查找，就可以根 据 target 和当前元素的大小关系来缩小查找区间，当前元素的查找区间为左下角的所有元素。

 

public class Solution {
    public boolean Find(int target, int [][] array) {
       int rows=array.length;
       int cols=array[0].length;
       int r=0,c=cols-1;
       while(r<=rows-1 && c>=0){
           if(target==array[r][c]){
               return true;
           }else if(target>array[r][c]){
               r++;
           }else{
               c--;
           }
           
       } 
        return false;
    }
}