从 FFT 到 NTT——快速处理卷积
前置知识
卷积
符号为 \(*\)。
设多项式 \(A(x) = a_0 + a_1x + a_2x^2 + \cdots + a_nx^n, B(x) = b_0 + b_1x_1 + b_2x^2 + \cdots + b_nx^n\),则有
即 \((A * B)[n]\) 的意义是将两个多项式相乘后 \(n\) 次项的系数。
单位复根
定义
我们把满足 \(\omega^n = 1\) 的复数 \(\omega\) 称为 \(n\) 次单位复根,不难得到 \(n\) 次单位复根有 \(n\) 个。
由欧拉公式 \(e^{ix} = \cos x + i \sin x\) 可推知 \(e^{2\pi i} = \cos 2\pi + i\sin 2\pi = 1\),进而可以得到主 \(n\) 次单位根 \(\omega_n\) 的表达式:
任意 \(n\) 次单位复根都是主 \(n\) 次单位复根的整次幂,记作 \(\omega_n^k (0 \le k \le n - 1)\) 。
不难得出:
性质
-
特殊值:\(\omega_{2n}^n = -1, \omega_n^0 = \omega_n^n = 1(n \in \N^*)\)。
-
消去引理:
\[\omega_{dn}^{dk} = \omega_n^k (n, k, d \in \N^*) \] -
折半引理(前提条件:\(n\) 为偶数):
\[\omega_n^{k + \frac n 2} = \omega_n^k \times \omega_n^{\frac n 2} = -\omega_n^k \] -
求和引理:
\[\sum_{j = 0}^{n - 1}(\omega_n^k)^j = \begin{cases} 0, k \ne 0 \\ n, k = 0 \end{cases} \]
多项式的表示方法
系数表示法
以 \(A(x) = a_0 + a_1x + a_2x^2 + \cdots a_{n - 1}x^{n - 1}\) 描述的多项式。
点值表示法
若 \(A\) 为 \(n\) 次多项式,则以 \(y = A(x)\) 的图像上任意不同的 \((n + 1)\) 个点可将其唯一确定。
也即 \(A\) 可用点值表示法表示为 \(\{(x_i, y_i)~|~ 0 \le i \le n\}\)。
快速傅立叶变换(FFT)
作用
快速地将一个以系数表示法描述的多项式转化为以点值表示法描述的形式。
流程
令 \(n = 2^k, k \in \N^*\)。
现有一多项式 \(A(x) = \sum\limits_{i = 0}^{n - 1} (a_ix^i)\),考虑将其化为两个项数为 \(\dfrac n2\) 的多项式,即:
则有:
将 \(x = \omega_n^0, \omega_n^1, \cdots, \omega_{n}^{n - 1}\) 依次代入求得对应值。此时再套上 消去引理 和 折半引理,可以发现些有趣的性质。这里以 \(\omega_n^k(0 \le k < \frac n 2)\) 为例:
- 若通过递归的方式求解 \(A(\omega_n^k)\),\(n\) 每次都会减小 \(\dfrac 1 2\),时间复杂度为 \(\mathcal O(\log n)\)。
- \(A(\omega_n^k)\) 和 \(A(\omega_n^{k + \frac n 2})\) 的递归式只有一项常数不同,在 \(\mathcal O(\log n)\) 求解 \(A(\omega_n^k)\) 时可以 \(\mathcal O(1)\) 求出 \(A(\omega_n^{k + \frac n 2})\)。
优化
在递归版 FFT 的执行过程中,底层会反复进行出入栈操作,导致常数巨大,由此引出了迭代版 FFT。
我们定义在已知 \(A_0(\omega_\frac n2^k)\) 和 \(\omega_n^k A_1(\omega_\frac n2^k)\) 的情况下,\(\mathcal O(1)\) 求出 \(A(\omega_n^k)\) 和 \(A(\omega_n^{k + \frac n2})\) 的操作为一次 蝴蝶操作。
假设我们现在知道 FFT 迭代树中叶子的顺序。那么只需要模拟回溯的合并过程,可以就着代码理解迭代过程:
具体来说:
- \(A_0(\omega_{\frac n2}^k)\) 存在下标 \(k\) 处,\(A_1(\omega_{\frac n2}^k)\) 存在下标 \(k + \frac n2\) 处。
- \(A(\omega_{n}^k)\) 存在下标 \(k\) 处。
因此,利用蝴蝶操作,我们可以直接在原位置覆盖,不需要开新的数组。
可以就着代码理解:
for (int i = 1; i < len; i <<= 1) { // 枚举单段区间长度
Complex wn = {cos(PI / i), flag * sin(PI / i)}; // 求出主 n 次单位根
for (int j = 0; j < len; j += (i << 1)) { // 两段两段区间地枚举(便于合并)
Complex w = {1, 0};
for (int k = j; k < j + i; k++) { // 枚举区间内值并进行蝴蝶操作
Complex t = w * A[k + i]; // 求出后面的一项
// 注意:一定要先覆盖 A[k + i],因为 A[k] 会在 A[k + i] 的覆盖中用到
A[k + i] = A[k] - t;
A[k] = A[k] + t;
w = w * wn;
}
}
}
那么应如何求出叶子的顺序呢?
这就引出了另一个重要的定理—— 蝴蝶定理。
首先,我们可以画出迭代树,它大概是长这样:
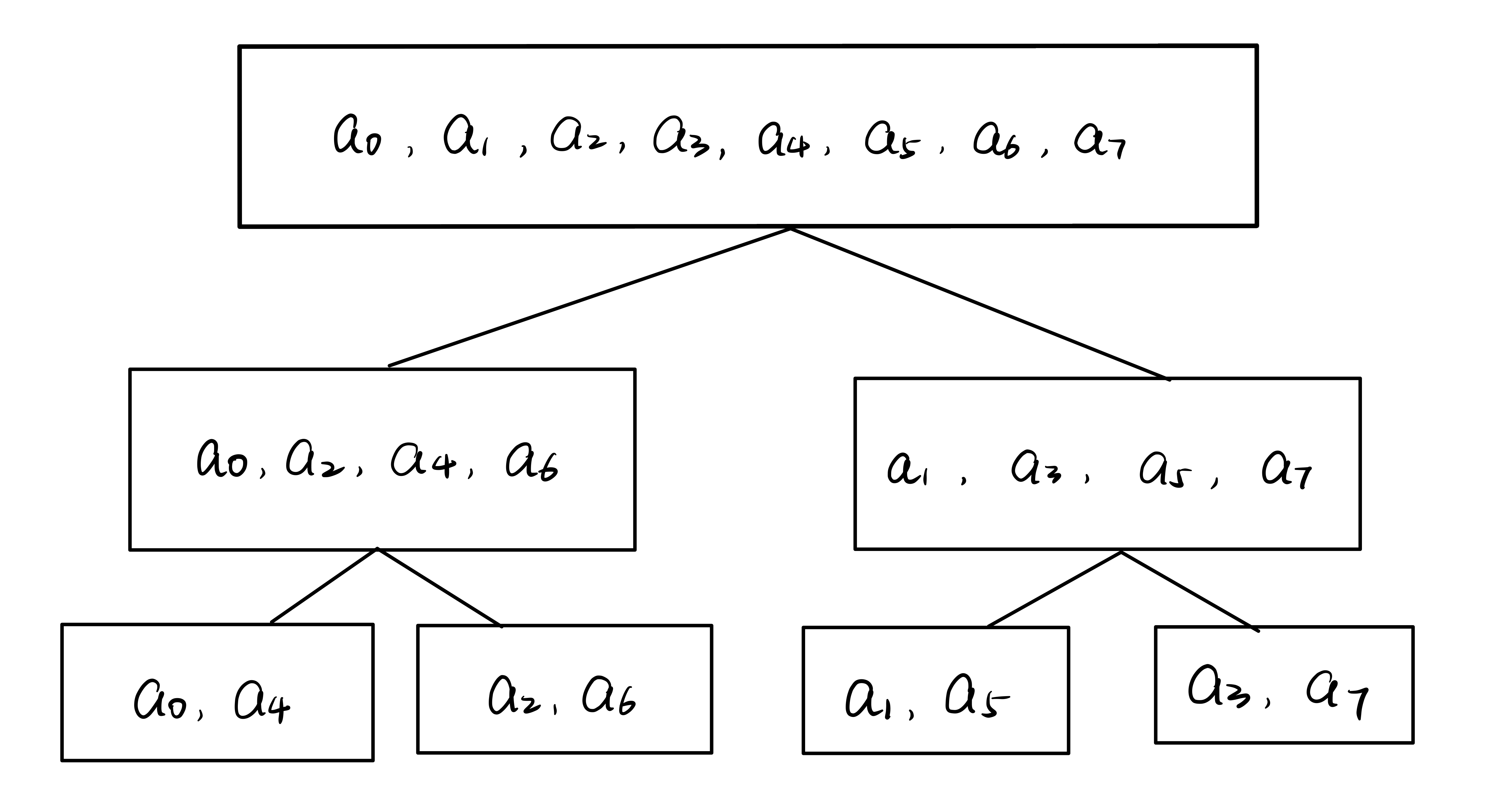
然后把叶子序列单拎出来和原序列对照着看,也就是:
0 1 2 3 4 5 6 7
0 4 2 6 1 5 3 7
再都换成二进制:
000 001 010 011 100 101 110 111
000 100 010 110 001 101 011 111
不难发现后者的每一项是前者对应项的反序,那么叶子序列也就可求了(求解叶子序列的位运算的式子特别难推,背板即可)。
设序列中最大值的二进制位数为 \(bits\),叶子序列为 \(rev\),则可以通过如下代码 \(\mathcal O(n)\) 求出叶子序列:
for (int i = 0; i < len; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bits - 1));
\(len\) 为满足 \(2^k \ge n + m\) 的最小的 \(2^k (k \in \N^*)\)。
于是有了 FFT 的代码:
void FFT(Complex A[]) {
for (int i = 0; i < len; i++) if (rev[i] > i) swap(A[i], A[rev[i]]); // if 保证只换一次
for (int i = 1; i < len; i <<= 1) {
Complex wn = {cos(PI / i), sin(PI / i)};
for (int j = 0; j < len; j += (i << 1)) {
Complex w = {1, 0};
for (int k = j; k < j + i; k++) {
Complex t = w * A[k + i];
A[k + i] = A[k] - t;
A[k] = A[k] + t;
w = w * wn;
}
}
}
}
时间复杂度
FFT 实际上就是一种类似于线段树的二分分治做法,时间复杂度为 \(\mathcal O(n \log n)\)。
快速傅立叶逆变换(IFFT)
推导过程
设我们上面求得的点值表示法下 \(A(x)\) 可表示为 \(\{(\omega_n^k, y_k)~|~ 0 \le k < n\}\)。
那么把 FFT 的过程写成矩阵乘法的形式就是:
要想求得 \(a_0, a_1, a_2, \cdots, a_{n - 1}\),只要等式两边同时乘上第一个大矩阵(范德蒙德矩阵)的逆矩阵即可。
考虑到范德蒙德矩阵和其逆矩阵 \(T\) 相乘后应为单位阵,即:
矩阵乘法后的结果只有 \(0, 1\) 两种取值,由此想到上面提到的 求和引理。
将范德蒙德矩阵每一项取倒数后与其相乘,则有:
于是有:
令 \(\theta = \dfrac{2k\pi i}n\),则 \(\dfrac 1{\omega_n^k} = \omega_n^{-k} = e^{i\theta} = \cos(-\theta) + i\sin(-\theta) = \cos \theta - i\sin\theta\),所以可以在 FFT 的代码中加入一个表示 \(i \sin\theta\) 符号的参数 \(flag\),\(flag = 1\) 时为 FFT,\(flag = -1\) 时为 IFFT。
代码:
void FFT(Complex A[], int flag) {
for (int i = 0; i < len; i++) if (rev[i] > i) swap(A[i], A[rev[i]]);
for (int i = 1; i < len; i <<= 1) {
Complex wn = {cos(PI / i), flag * sin(PI / i)}; // 整个函数唯一一次用到 flag
for (int j = 0; j < len; j += (i << 1)) {
Complex w = {1, 0};
for (int k = j; k < j + i; k++) {
Complex t = w * A[k + i];
A[k + i] = A[k] - t;
A[k] = A[k] + t;
w = w * wn;
}
}
}
}
时间复杂度
显然与 FFT 相同,为 \(\mathcal O(n \log n)\)。
快速数论变换(NTT)
引入
在 FFT 中,我们利用了单位复根的优秀性质把系数表示法和点值表示法的互换从 \(\mathcal O(n^2)\) 优化到了 \(\mathcal O(n \log n)\),但是因为用到了浮点数,FFT 无论是从常数上还是精度上都不那么理想。
有没有什么东西能代替复数呢?
还真有,叫 原根,它与 阶 密不可分。
阶
若 \(a, p\) 互质,且 \(p > 1\),对于 \(a^n \equiv 1 \pmod p\) 的最小的 \(n\),称 \(n\) 为 \(a\) 模 \(p\) 意义下的 阶,记作 \(\delta_p(a)\)。
例如:\(\delta_7(2) = 3\),因为 \(2^1 \bmod 7 = 2, 2^2 \bmod 7 = 4, 2^3 \bmod 7 = 1\)。
性质:
-
若 \(a, p\) 互质且 \(p > 1\),对于 \(a^n \equiv 1 \pmod p\),一定有 \(\delta_p(a)|n\)。证明显然。
-
\(\delta_p(a)|\varphi(p)\)
证明:由欧拉定理得 \(a^{\varphi(p)} \equiv 1 \pmod p\),又由第一条性质,得证。
原根
若 \(\delta_p(a) = \varphi(p)\),则称 \(a\) 为模 \(p\) 意义下的一个 原根。
例如:\(\delta_7(3) = 6 = \varphi(7)\),所以 \(3\) 是 \(7\) 的一个原根。
一个正整数 \(m\) 有原根的充要条件是 \(m = 2, 4, p^n, 2p^n\),其中 \(p\) 为奇素数,\(n\) 为正整数。
如何求一个大质数的原根?
原根一般都很小,所以可以从枚举 \(g\),枚举求 \(\delta_p(g)\) 太慢了,不妨利用阶的性质,枚举 \(\varphi(p)\) 的因数,这样单次求 \(\delta_p(g)\) 就是 \(\mathcal O(\sqrt p)\) 的了,实际实现的话很快就能求出原根。
既然想用原根替代单位复根,就要让原根具有单位复根一样的性质,即满足:
- \(\omega_{2n}^{2k} = \omega_n^k\)
- \(\omega_{n}^{k + \frac n2} = -\omega_n^k\)
- \(\sum\limits_{j = 0}^{n - 1}(\omega_n^k)^j = \begin{cases}n & k = 0 \\ 0 & k \ne 0 \end{cases}\)
结论:\(\omega_n \equiv g^{\frac{p - 1}n} \pmod P\)。
所以中 NTT 对模数 \(P\) 的一个硬性要求就是 \(2^{\lceil \log n \rceil} | (P - 1)\)。
所以在 NTT 中,我们一般用 \(P = 998244353\) 作模数,因为 \(998244353 = 2^{23} + 7 \times 17 + 1\),\(\mathcal O(n \log n)\) 的算法一般最多跑到 \(n \le 10^6\),而 \(2^{23} > 8 \times 10^6\),完全够用,它的一个原根是 \(g = 3\)。
剩下的就跟 FFT 一样啦~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号