Knight Tour Problem

哈密顿图

它是一个无向图，由天文学家哈密顿提出，由指定的起点前往指定的终点，途中经过所有其他节点且只经过一次。在图论中是指含有哈密顿回路的图，闭合的哈密顿路径称作为哈密顿回路，含有图中所有顶点的路径称作为哈密顿路径。

骑士巡逻(Knight's tour)

骑士巡逻是指按照国际象棋中骑士的规定走法走遍整个棋盘的每一个方格，而且每一个网格只能经过一次。假若骑士能够重新走回最初的位置，则称此巡逻为封闭巡逻，否则，称为开巡逻。

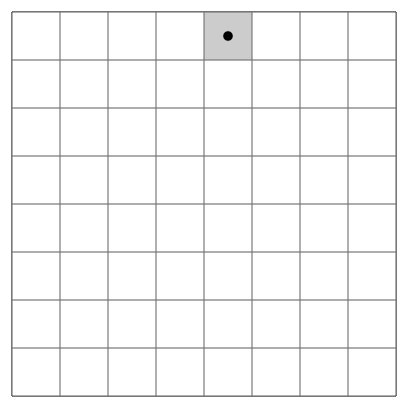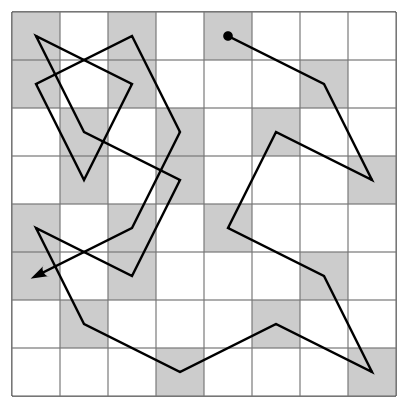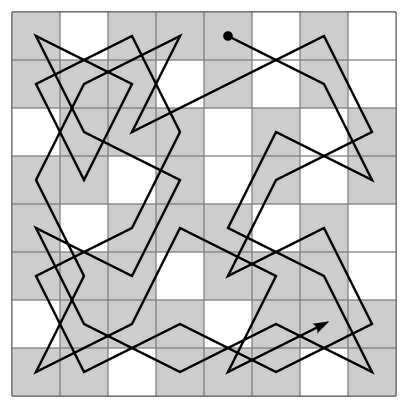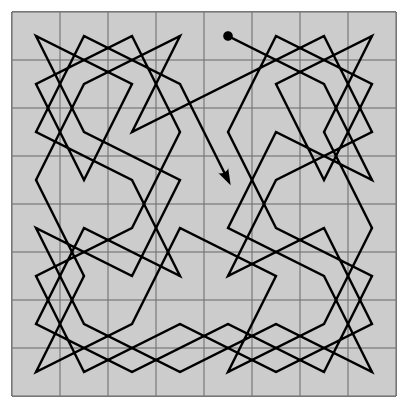
Knight's Tour Problem

Description :

The knight is placed on the first block of an empty board and , moving according to the rules of chess, must visit each square exactly once

Following is chessboard with 8 * 8 cells. Numbers in cells indicate move number of Knight.

注： 上面8 * 8 的表格表明一条路径，由 0 -> 1 -> 2 …… -> 63， 即由左上角->右上角

Backtracking Algorithm for Knight's tour

If all squares are visited 
	print the solution 
Else 
	a) Add one of the next moves to solution vector and recursively
	check if this move leads to a solution.(国际象棋中骑士只有8中走法，每次选择其中的一种)
	b) If the move chosen in the above step doesn't lead to a solution then remove this move from the solution vector and try other alternative moves
	c) If none of the alternatives work then return false("No solution exists")

Source code

#include <stdio.h>
#include <stdbool.h>

#define N 8

int solveKTUtil(int x, int y, int movi, int sol[N][N], int xMove[], int yMove[]);

/*
 * A utility function to check if i,j are valid indexes
 * for N * N chessboard
 */
bool isSafe(int x, int y, int sol[N][N])
{
    return (x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1);
}

/*
 * A utility function to print solution matrix sol[N][N]
 */
void printSolution(int sol[N][N])
{
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            printf(" %2d", sol[i][j]);
        }
        printf("\n");

    }
}

/*
 * This function solves the Knight tour problem using Backtracking
 * This function mainly uses solveKTUtil() to solve the problem
 * It return false if no complete tour is possible
 * otherwise return true and prints the tour
 * Note: this function prints one of the feasible solutions.
 */
bool solveKT()
{
    int sol[N][N];
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            sol[i][j] = -1;
        }
    }
    /* xMove[] and yMove[] define next move of Knight.
       xMove[] is for next value of x coordinate
       yMove[] is for next value of y coordinate */
    int xMove[8] = {  2, 1, -1, -2, -2, -1,  1,  2 };
    int yMove[8] = {  1, 2,  2,  1, -1, -2, -2, -1 };

    // Since the Knight is initially at the first block
    sol[0][0]  = 0;

    /* Start from 0,0 and explore all tours using
       solveKTUtil() */
    if (solveKTUtil(0, 0, 1, sol, xMove, yMove) == false)
    {
        printf("Solution does not exist");
        return false;
    }
    else
        printSolution(sol);

    return true;
}

/* A recursive utility function to solve Knight Tour
   problem */
int solveKTUtil(int x, int y, int movei, int sol[N][N],
                int xMove[N], int yMove[N])
{
    int k, next_x, next_y;
    if (movei == N*N)
        return true;

    /* Try all next moves from the current coordinate x, y */
    for (k = 0; k < 8; k++)
    {
        next_x = x + xMove[k];
        next_y = y + yMove[k];
        if (isSafe(next_x, next_y, sol))
        {
            sol[next_x][next_y] = movei;
            if (solveKTUtil(next_x, next_y, movei+1, sol,
                            xMove, yMove) == true)
                return true;
            else
                sol[next_x][next_y] = -1;// backtracking
        }
    }

    return false;
}

int main(int argc, char *argv[]){
    solveKT();
    return 0;
}

Output

  0  59  38  33  30  17   8  63
 37  34  31  60   9  62  29  16
 58   1  36  39  32  27  18   7
 35  48  41  26  61  10  15  28
 42  57   2  49  40  23   6  19
 47  50  45  54  25  20  11  14
 56  43  52   3  22  13  24   5
 51  46  55  44  53   4  21  12

主要内容源自https://www.geeksforgeeks.org/?p=12916