Codeforces Round #560 (Div. 3)

A. Remainder

这题唯一的坑点就是x哪一位不用判断是否为1，我就跳了进去

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long

int main(){
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	int n,x,y;
	while(cin>>n>>x>>y){
		string s;
		cin>>s;
		int l=s.length(); x++,y++; 
		int cnt=1,sum=0;
		for(int i =l-1 ;i>=0;i--){
			//cout<<cnt<<' '<<s[i]<<endl;
			if(cnt<y) {
				if(s[i]=='1') sum++ ;
			}
			else if(cnt==y&&s[i]=='0') sum++;
			else if(cnt>y&&cnt<x) {
				if(s[i]=='1') sum++;
			}
			else if(cnt==x){
			//	if(s[i]=='0') sum++;
				break;
			}
			cnt++;
		}
		cout<<sum<<endl;
	}
	return 0;
}

B. Polycarp Training

我写的复杂了
每次都从某个位置开始lower_bound
统计就好了

代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int a[N];
int main(){
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	int n;
	while(cin>>n){
		for(int i=0;i<n;i++)
		cin>>a[i];
		sort(a,a+n);
		int ans,ba=0;
		for(int i=1;;i++){
			int p=lower_bound(a+ba,a+n,i)-a;
			if(p==n) break;
			else ans=i;
			ba=p+1;
			if(ba==n) break;
		}
		cout<<ans<<endl;
	} 
	return 0;
}

C. Good String

直接暴力贪心往后删就ok了

代码

#include<bits/stdc++.h>
using namespace std;
int main(){
	int n;
	string s;
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	while(cin>>n){
		int sum=0;
		cin>>s;
		int j;
		for(int i=0;i<n-1;i=j+1){
			 j=i+1;
			while(j<n){
				if(s[i]!=s[j]){
					 break;
				}
				else{
					sum++; s[j]='*'; j++;
				}
			}
		}
		//cout<<sum<<endl;
		if((n-sum)&1){
			sum++; 
			cout<<sum<<endl;
			sum=n-sum;
			for(int i=0;i<n;i++)
			if(s[i]!='*'&&sum){
				cout<<s[i]; sum--;
			}
			cout<<endl;
		}
		else{
			cout<<sum<<endl;
			for(int i=0;i<n;i++)
			if(s[i]!='*')
			cout<<s[i];
			cout<<endl;
		}
	}
	return 0;
}

D. Almost All Divisors

这题明显就是考察数学的了
对于任何数你把所有因子全列出来。
并对因子排序。
d[i]*d[x-i+1]就等于这个数了。
然后就对给的所有因子都检查一遍，是否都包含在里面

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll a[410];
int main(){
	int t,n;
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
		scanf("%lld",&a[i]);
		sort(a+1,a+n+1);
		ll ans=a[1]*a[n];
		bool ok=1;
		for(int i=1;i<=n;i++)
		if(a[i]*a[n-i+1]!=ans) {
			ok=0; break;
		}
		for(ll i=2;i*i<=ans;i++)
		if(ans%i==0){
			n--;
			if(i*i!=ans)
			n--;
		}
		if(ok&&!n) printf("%lld\n",ans);
		else puts("-1");
	}
	return 0;
}`

E. Two Arrays and Sum of Functions

[http://codeforces.com/contest/1165/problem/E]
题意
给你两个长度相同长度的数组。
你只能重排第二个数组使得

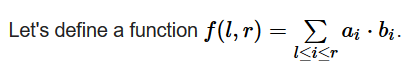
对于所有的l<=r上面表达式之和最小。

分析

首先一旦两个数组固定之后每个a[i]b[i]根据位置他们加的次数是一定的。假设是x次
那么该位置的贡献是xa[i]b[i]因为a[i]是固定的所以xa[i]是固定的。
你可以把a[i]=xa[i].那么只要对a,b一个大到小，一个小到大排相乘即可以了。
哪个次数我是找规律得到的。x=i(n-i+1);

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+10;
const ll mod=998244353;
ll a[N],b[N];
bool cp(ll x,ll y){
	return x>y;
}
int main(){
	int n;
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	while(cin>>n){
	   for(int i=1;i<=n;i++)
	   {
	   	cin>>a[i]; a[i]=(a[i]*i*(n-i+1));
	   }
	   for(int i=1;i<=n;i++)
	   cin>>b[i];
	   sort(a+1,a+n+1);
	   sort(b+1,b+n+1,cp);
	   ll ans=0;
	   for(int i=1;i<=n;i++)
	   ans=(ans+a[i]%mod*b[i]%mod)%mod;
	   cout<<ans<<endl;
	}
	return 0;
}

F1+F2. Microtransactions (hard version)

[http://codeforces.com/contest/1165/problem/F2]
题意
我转换一下，
有n种物品，有m种优惠。
每种物品都有a[i]个
初始物品都是两个金币
某种优惠是某一天某种物品价格打五折。
然后你每天开始你会获得1个金币。
问你最少需要多少天能把所有的物品买完

分析

这题的难点在于，如何二分，还有就是贪心。
我都注释在代码了，看看就知道了
至于为什么从后面的天开始看一下这组数据
2 3
1 1
1 1
1 2
2 1
如果你从前往后就得3天，后往前就两天。
就是前往后你当前的金币是不能最大化的。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
vector<int> ve[2*N];
int a[N],b[N],sum=0;
bool ok(int m,int n){
	int res=sum;//剩下的没购买的 
	int dres=0;//最后统计剩下的钱
	//m表示当前剩下的钱 
	for(int i=1;i<=n;i++) b[i]=a[i];
	for(int i=m;i>=1;i--){
		for(int j=0;j<ve[i].size();j++)
		while(m&&b[ve[i][j]]){
			m--,b[ve[i][j]]--;
			res--;
		}
		if(m>=i){//关键这里
		//如果当前剩下的钱不能在以后优惠的时间使用就只能原价买了 
		int c=m-i+1; 
			m-=c,dres+=c;
		}
	}
   return dres/2>=res;
}
int main(){
	int n,m,d,t;
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	cin>>a[i],sum+=a[i];
	for(int i=0;i<m;i++){
		cin>>d>>t;
		ve[d].push_back(t);
	}
	
	int l=sum,r=sum*2,ans;
	while(l<=r){
		int m=(l+r)>>1;
		if(ok(m,n)){
			ans=m,r=m-1;
		}
		else l=m+1;
	}
	cout<<ans<<endl;
	return 0;
}