计算机系统数据表示

计算机里面的基本单位有哪些？

• 位：bit，二进制数（binary digit）的英文缩写
• 字节：Byte，8位
• 字：计算机的字由两个或多个相邻字节构成，处理器访问和处理的时候是按照字为单位进行，即这些字节被当做一个整体处理。字的大小（Word size）表示特定架构有效处理的数据最大大小，常见大小有16位32位64位。
  • 比如16位可以表示的有符号位的最大整数是32767，32位可以表示的无符号位最大整数4294967295即2³²即内存大小限制4G，毕竟是要寻址的，再大无法表示地址。
  • 32位操作系统int类型的最大值是 2147483647。 在32位操作系统下int类型取值范围如下： Int32 //等于int, 占4个字节（-2147483648~2147483647）
• 半字节：8位字节可以对半分为两个4位，称为半字节，
  • 低半字节、高半字节：包含最小值二进制数字的半字节称为低半字节，另外半个字节为高半字节。

按位计数系统是什么？

positional numbering systems

数字的值可以通过增加基数（基或底radix）的幂来表示，也叫做加权计数系统weighted numbering system（每个位置是通过基数的幂加权得到的）

基数为n，则有效的数字为0到n-1这n个数字，可以将基数写在右下角来表示采用的计数系统

无符号整数的表示方法？

• 重复减法，这个其实是最快的以后用到的，熟记2进制里面八位每一位对应的十进制，从最高开始比较，就可以快速写出小于255的整数的二进制形式
• 
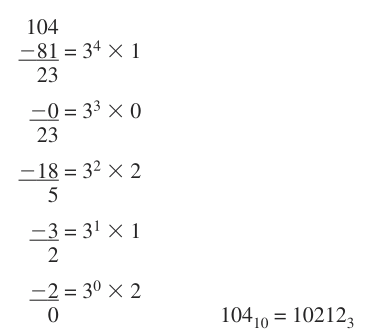
• 除法-余数。
• 

什么是溢出？

• 一个N位的二进制数可以表示从0～2^N-1范围内的无符号十进制整数。当对无符号的二进制数进行算数预算，结果超出给定位数的二进制数所能表示的数值范围，称作溢出。

分数（小数）进制转换？

• 重复减法：减去 基数的负幂 加权
• 
• 乘法-整数：先转换为十进制，再依次乘以基数取整数部分
• 

小数进制转换为什么说“用基数的负指数幂近似表示分数”？

十进制的分数自己本身转为小数的时候也会出现循环小数或者无限不循环小数，进制转换的时候，由重复减法可以看出来，因为每一次减去的是基数的负幂  加权，大多数情况是不能正好表示出来，一般都是近似值，只是达到精度要求就停止继续往下减

2/3在十进制中是无限循环小数，而在三进制中则表示为0.2(3)，即2*3^(-1)不再有数字循环

2、8、16进制相互转换？

二进制通常使用十六进制表示来增加可读性

从一个基转换为另一个基

• 2-》8：3个一组
• 2-》16：4个一组
• 8-》2：1个顶三
• 16-》2：1个顶四

无符号数的进位和溢出关系？

位的总数不够大不足以保存结果，发生溢出。进位是前提，溢出是结果，最左边位进位出来的

有符号数的表示方法？

二进制整数部分 原码补码反码表示方法：

• 原码：将最高位作为符号位（以0代表正，1代表负），其余各位代表数值本身的绝对值（以二进制表示）。

+7的原码为： 00000111

-7的原码为： 10000111

• 反码：一个数如果为正，则它的反码与原码相同；一个数如果为负，则符号位为1，其余各位是对原码取反。

+7的反码为：00000111

-7的反码为： 11111000

• 补码：一个数如果为正，则它的原码、反码、补码相同；一个数如果为负，则符号位为1，其余各位是对原码取反，然后整个数加1。为了简单起见，我们用1个字节来表示一个整数：

+7的补码为： 00000111

-7的补码为： 11111001

二进制小数部分 原码补码反码表示方法：

• 原码：一样
• 反码：一个数如果为正，则它的反码与原码相同；一个数如果为负，则符号位为1，其余各位是对原码取反。

正数的反码为：本身

负数x的反码为： 2-2^-n + x

• 补码：

正数的补码为： 本身

负数x的补码为：2+x，例如-0.1对应的补码为10.0-0.1=1.0

原码补码反码表示原理

• 原码：N位能够表示的范围为-2^(N-1)+1~2(N-1)-1，八位字可表示整数范围-127～127。通过这种方法表示0会有两种可能：10000000或00000000，造成逻辑和电路上的复杂性。
• 补码：时钟指向6点，想要指向3点，可以-3圈，也可以+9圈。这里的-3和+9对于时钟的作用是一致的。对于他们而言，在时钟整体的运行机制中模就是12。如果是15点则12会自动丢失，留下3。
  • 只要确定了模，就找到了与负数等价的正数（这个正数就是负数对于模的补数），用这个正数来代替负数把减法运算用加法实现。
  • 正数相对于模的补数是他本身，负数相对于模的补数是“模-|负数|”
  • 在r进制中，如果被减数有d位数字，如果数字N ≠ 0，减数N的补码定义为r^d - N，如果N = 0，则N的补码就是0。(这是补码有含义的计算方式，上面的表示方法只是值一样)
• 反码：在r进制中，如果规定有d位数字，则数字N，的反码为（r^d - 1）- N。
  • 对于十进制数，r=10，则2468的反码就是10^4 - 1 - 2468 = 7531。
  • 对于二进制来说，只需要将所有位翻转。

二进制原码补码反码运算方法

运算过程中，不同的符号位和数值位构成的编码决定了运算的不同方式，即原码补码反码由于符号位和数值位的含义不同，在运算时遵循的规则也不一样

• 原码：
  • 如果符号相同，大小相加，结果取相同的符号；
  • 如果符号相反，先比较幅值的大小，符号位由幅值较大的操作数决定，幅值为大幅值减去小幅值；
  • 从右往左算术运算，加法可能进位，减法可能借位，如果最高位有进位则说明发生了溢出。
• 补码：先把减法转换为补码对应的加法，相加之后得到补码，如果是正数就直接转换为十进制，如果是负数，先减1，在除去首位全部翻转，得到原码，再转换为十进制
• 反码：其算术运算规则遵循高低两端进位循环（end carry-around）：如果最高位有进位（0或1），就把进位加到最低位上。

有符号数的进位和溢出关系？

如果进入符号位和从符号位出来的进位不同，就是发生溢出

整数乘除运算方法

乘法运算

• 竖式运算：写一个十进制竖式就明白二进制的了，是一样的。设置一个指针指向乘数的最低位，从右向左读，指针每向左移动一位，被乘数也整体左移一位。结果初始化时为0，根据指针指向的乘数当前位是否为1决定是否加上被乘数。
• 移位运算：乘2的幂，相当于左移幂个位置；
  • 算术左移：符号位发生改变，操作溢出，说明两个数相乘的结果用现有的位数不足以表示。例如使用8位有符号数的2的补码来表示数据，求66*2。对应01000010，左移之后是10000100，太大变成负数发生溢出，使用9位有符号数的2的补码表示就不会溢出

除法运算

• 迭代从被减数减去分母：整数除法和浮点除法有显著区别，可能引起计算机系统崩溃，如尝试除以0，或者两个操作数大小相差悬殊。当除数远小于被除数时，会产生“除法下溢”，即被等效视为被0除。
• 移位运算：除以2的幂，相当于右移幂个位置，余数不能被存储
  • 算术右移：左边补得数字和符号位一致
  • 是整数除法，-15/2得到的是-8

浮点表示法：  

采用浮点仿真，浮点数由三部分组成，符号位、指数部分（2的幂指数，指数部分的二进制一般使用移码来表示）、小数部分（有叫有效数或者尾数，小数部分写的时候按照规格左边第一位必须是1写完之后后面补0直到占满位数即可）。

对于14位模型，最高位为符号位，之后5位为指数位，最后8位为有效数。

明确这里用的是整数来模拟浮点运算，在软件的角度来解决问题，FPU是从硬件的角度解决问题。浮点运算器（floating point unit，缩写FPU）是运行浮点运算的结构。一般是用电路来实现，应用在计算机芯片中。是整数运算器之后的一大发展，因为在浮点运算器发明之前，计算机中的浮点运算是都是用整数运算来模拟的，效率十分不良。浮点运算器一定会有误差，但科学及工程计算仍大量的依靠浮点运算器——只是在程序设计时就必需考虑精确度问题。

什么是移码？

用于整数来模拟浮点数的时候，指数使用移码来表示，防止负指数幂无法表示。以偏移值作为基准0，小于偏移值为负数，大于偏移值为正数，偏移值一般通过表示的最大位数除以2 来得到

所以一个有5位的二进制数，可以表示最大32，那么0-31是范围，分成两半0-15和16-31，0-15为负数，16到31为正数，则偏移量为15（大家都相对于0偏移），则偏移值为15的移码表示方法就是：给定数字5，他的移码就是5+15=20，给定-1，他的移码就是-1+15=14。这样负指数就表示出来了

浮点运算方法：

• 对于加减法，先将参与运算的两个数表示成具有同一基数的相同指数形式，然后通过移位将两个数对齐，得到的结果重新进行规格化处理，保留较大的指数。
• 乘法和除法采用与十进制相同的法则。

什么是浮点误差？

使用的位数越多，表示越精确。

例如一个14位模型，对应的浮点模型就是1个符号位，5的指数位，8个有效数，想要保存128.5的时候，对应的二进制数字是10000000.1，一共9位，但是只有8位有效数，所以最低阶的数字就会丢弃最终出来的是10000000.0，后面的0还会出来是因为指数域并没有丢失，所以只是把低阶丢失得到了一个近似值

无论系统设计的多么大，用有限的系统表示实数集必然会引入不同程度的浮点误差。误差会传递，可能引起严重偏差。

什么是IEEE-754浮点标准？

IEEE制订了关于浮点数的表示标准IEEE-754，指定表示和运算浮点数的标准

• 单精度浮点数标准：总字长为32位。偏移量127（即指数域有8位，所以移码的偏移量为127，大于127位正数，小于为负数），如果指数超出偏移量，则使用正负无穷大或NaN表示（一个非实数的值，通常用作错误标识）；
• 
• 双精度****浮点数标准：总长64位。采用11位指数和52位有效数字，偏移量1023，指数为2047时表示NaN。

无论单双精度都有两种表示0的方法，当指数部分和有效数都为0时，无论符号位都是0

• 

表数范围、精度和准确度的区别是什么？

表数范围在上面图中间隔线可以找到，

精度是使用多少信息来表示一个数字

准确度是表示的数字和真实值之间的差距，精度和准确度之间没有准确关系，无限不循环小数的准确度取决于精度。

浮点错误不是很理解。。

https://blog.csdn.net/a519781181/article/details/52412024

字符编码

• 二进制编码的十进制数（binary-coded decimal，BCD）：最初在IBM主流机型和中间过渡机型上使用，将每个十进制数字编码成一个4位的二进制数形式。如果按照8位字节的形式存储，则高4位称为区位（zone），低四位称为数字（digit）。主流BCD包含属于位置编码系统的8421码，5421码，2421码，以及非位置编码系统的余3码，格雷码。8位存储时的区位分别为1111（无符号数），1100（正数），1101（负数）。因为BCD编码数的数字只占半字节，因此多个相连的数字放入相邻的半字节时只需要留下一个5位的半字节作为符号，这个过程称为压缩。
  • EBCDIC：在开发IBM System/360前，IBM一直使用6位BCD编码表示字符和数字。为保证兼容性，后来采取了扩展的二-十进制编码的交换代码，将6位拓展到8位。
  • ASCII：美国信息交换标准代码（American Standard Code for Information Interchange）是从电传打字设备的编码方案中直接衍生出来的，20世纪60年代，ISO设计了一种7位的编码方案，称为第5国际字母。1967年成为官方标准。
  • 统一字符编码标准：1991年，统一字符编码协会建立了新的国际信息交换代码Unicode，为16位编码字母表，可以向下兼容ASCII码和拉丁-1字符集，并与ISO/IEC 10646-1国际字母表相一致，能够对全世界所使用的每一种语言的大多数字符进行编码。统一字符编码目前是美式计算机系统唯一使用的字符编码。

2. 用于数据记录和传递的编码方式（在把宿舍写入到某种类型的记录介质如磁带或磁盘，或者将数据进行长距离传送时，二进制信号可能会变得模糊不清，尤其是一长串的0或1）：
   • 不归零编码（non-return-to-zero，NRZ）：用高电压表示1，低电压表示0。对于长串的0或1，如果接收器同步较慢或者定时系统发生错位，很容易丢失编码。
   • 反转不归零编码（non-return-to-zero-invert，NRZI）：采用信号的转变，或者从高到低，或者从低到高的变化表示二进制的1，没有变化则表示0。虽然消除了二进制数1的丢失问题，但仍面临长串0的问题。
   • 相位调制编码（phase modulation，PM），对编码的每一位都提供一个信号转变，二进制1由上升转变的信号给出，0则伴随一个下降转变的信号（如果需要，还会在每个位单元的边界提供一个额外的信号转变）。相位调制编码通常用于数据传送，如局域网，但不足以运用于数据存储，因为PM需要两倍于NRZ编码的位数。
   • 频率调制编码（frequency modulation，FM），类似于相位调制编码，在每个位单元中至少提供一个信号跃变，这些同步的跃变发生在每个位单元的开始处，除此之外如果对二进制1编码，还要在位单元的中间提供一个额外的信号跃变。相对于数据存储而言，FM只是比PM好一点。FM可以延伸出一种改进的频率调制（MFM），这种方法只对具有连续的0的编码才在位单元的边界提供信号跃变。因为MFM编码需要的信号跃变数比PM少，比NRZ多；错误控制和经济角度又较为高效，因此多年来MFM编码是硬盘存储中使用的唯一编码方式。
   • 运行长度限制编码（Run-Length-Limited，RLL）是一种对由字符编码组成的字进行分块的编码方式。比如把ASCII码或EBCDIC码翻译成一族特殊设计的编码字，限制连续0出现的数目，如RLL（d，k）编码允许在任何一对相邻的1之间出现最少d个，最多k个0。显然RLL编码字必须包含比原来的字符编码更多的位数，但RLL在磁盘上采用NRZI方式编码，因此RLL编码的数据在磁介质上占更少的空间，因为这种编码涉及到的磁通量的转变少的多。RLL（2,7）是磁盘系统中使用的主流编码方式，它是一个8位的ASCII或EBCDIC字符的16位映射，但比MFM编码高出50%的存储效率。理论上，RL是一种Huffman编码的数据压缩形式，核心思想是使用最短的编码字的位组合方式来对尽可能多的信息位的组合方式进行编码

错误检测与校正

1. 循环冗余码校验（cyclic redundancy check，CRC）可以决定在一大块或者一长串信息字中是否出现一个错误，要检测的数据字块的规模越大，要求的校验和就越大，并且需要对求校验和的方法提供某种适当的保护，求校验和的方法以及CRC方法都是一种系统性的误差检测（systematic error detection）方案，即将错误校验位夹在原始信息数据位的后面。组成错误校验位的位组合称为校正子。CRC采用模2算术，假设信息字节为I = 1001011（可以是任意大小的字节），发送器和接收器都对某个任意的二进制位组合模式达成协议，如P=1011（如该位组合模式的开始和结束位都是1则效果最好），记P的位数为n = 4，将I左移n-1位，并用新的I作为被除数，P作为除数进行模2除法，得到余数r，将余数r加到移位后的I上，组成要发送的信息M。在本例中，r = 100，I + r = M = 1001011100。接受端将M使用模2除法除以P，如果无法严格整除则传送过程中有错误发生。常用的P可以为CRC-CCITT（ITU-T）：0001 0001 0000 0010 0001；CRC-12：0001 0000 0000 1111；CRC-16（ANSI）：0001 1000 0000 0000 0101；CRC-32：1 0000 0100 1100 0001 0001 1101 1011 0011。前三种是对字节操作，CRC-32是对4字节操作，适用于32位字系统。
2. 海明编码（Hamming code）具有校正错误的能力，采用奇偶校验。普通的奇偶校验只能检错（且无法检测双位出错）无法纠错。通常使用在随机错误最可能发生的情形（假定每一位出错的几率都是固定的，与其他位的出错没有关联）。海明编码的奇偶校验位（冗余位）根据信息字本身的位数决定。最后形成的编码字由m位信息字本身和r位校验位组成，满足m + r + 1 <= 2^r。两个编码字之间不同的位的位置数目称为两个编码字的海明距离，对于一种编码方法中任意一对编码的最小海明距离（minimum Hamming distance），用D（min）表示。海明编码可以检测出D（min）-1个单位错误，能够纠正[（D（min）-1）/2]个错误。因此如果要纠正k个错误，最小海明距离必须大于2k+1。
   • 创建海明编码的方法：首先根据公式确定编码所需的校验位数目r，算出编码字的位长度n = m + r，从右向左从1开始编号。位数是2的指数幂的位设置为奇偶校验位，其他位为数据位。对于各个编码位置，第b位编码由满足b = b1 + b2 + … + bj的奇偶校验位b1，b2，…，bj检测。
     例如：对ASCII字符K编码，K为01001011，m=8，r=4。从1开始从右向左编号，第1，2，4，8位为奇偶校验位，1 = 1，2 = 2，3 = 2 + 1，4 = 4，5 = 4 + 1，6 = 4 + 2，……，10 = 8 + 2，11 = 8 + 2 + 1，12 = 8 + 4。因为第1、3、5、7、9、11位的求和表达式中含有1，所以第一位（最低位）的奇偶校验位将检测这几个位置的奇偶特性，同理，第2位对2、3、6、7、10、11位作用，第4位对4、5、6、7、12位作用，第8位对8、9、10、11、12作用。分别对各自对应的位数奇偶校验，产生编码字010011010110。假如在传递编码字的过程中发生了一个错误，如发生在第9位，则接收到的为010111010110。接受端可以发现第1位、第8位的奇偶校验位出错，而第2位、第4位没有出错。因此可以推测出出错的码位是1 + 8 = 9位。取反即可。海明编码在出错率非常低的正常情况非常有效，但如果发生成块的错误（相邻数据位），则无效。
3. 里德-所罗门编码（Reed-Soloman，RS）针对区块错误（突发错误），如因为操作不当和外界环境影响导致存储设备发生相邻数据位损坏。RS编码属于CRC类型的编码，是一种系统编码方式，在信息字节块上加入奇偶校验位。RS（n，k）编码中的参数定义为：s = 一个字符所占位的数目，k = 构成数据块的s位字符的数目，n = 编码字的位的数目。RS（n，k）可以在k个信息字节组成的编码字中校正（n-k）/2个错误。流行的RS（255,233）编码方式是采用223个8位信息字节加上32个错误校正字节构成255字节的编码字。