洛谷P5521 [yLOI2019] 梅深不见冬 「题解」

P5521 [yLOI2019] 梅深不见冬

题目背景

风，吹起梅岭的深冬；霜，如惊涛一样汹涌；
雪，飘落后把所有烧成空，像这场，捕捉不到的梦。
醒来时已是多年之久，宫门铜环才长了铁锈，也开始生出离愁。

——银临《梅深不见冬》

题目描述

扶苏从深冬的梅岭走出，来到了一棵有 \(n\) 个节点的有根树上。

如果你不知道什么是树，可以认为树是一个边数恰好比节点个数少一的简单无向连通图。

如果我们规定 \(x\) 是树 \(T\) 的根，那么定义任意一个节点 \(y\) 到根的路径就是从 \(y\) 出发不重复经过节点到达 \(x\) 所经过的所经过的点构成的点集。可以证明这样的点集有且仅有一个。

定义一个节点 \(u\) 是节点 \(v\) 的孩子，当且仅当 \(u\) 与 \(v\) 相连且 \(u\) 不在 \(v\) 到根的路径中。如果 \(u\) 是 \(v\) 的孩子，那么定义 \(v\) 是 \(u\) 的家长节点。

如果我是 @_rqy 那种毒瘤神仙的话，可能会问你每个节点的孩子数不超过 \(k\) 的 \(n\) 个节点的带标号无根树一共有多少个，可惜这个问题我也不会，所以我不会问你这么毒瘤的问题。

扶苏从这棵 \(n\) 个节点的树的 \(1\) 号节点出发，沿着树上的边行走。当然我们规定 \(1\) 号节点是这棵树的根。他所行走的规定是：当扶苏在节点 \(u\) 时，扶苏要么在 \(u\) 的孩子中选择一个没有到达过的节点 \(v\) 并行走到 \(v\)，要么选择回到 \(u\) 的家长节点。

现在给每个节点一个权值 \(w\)，其中 \(i\) 号节点的权值为 \(w_i\)。他想给这棵树的某个节点放上从梅岭带出的梅花。我们规定扶苏能在节点 \(u\) 放上梅花当且仅当满足如下条件：

扶苏当前在节点 \(u\)。

对于 \(u\) 的所有孩子 \(v\)，节点 \(v\) 被放上了 \(w_v\) 朵梅花。

同时，扶苏可以在任意时刻收回任意节点上的梅花，在收回梅花时不需要走到对应节点。

现在扶苏想问问你，对于每个节点，如果他想在 \(i\) 号节点上放 \(w_i\) 朵梅花，那么他最少要从梅岭带出多少朵梅花。

输入格式

每个输入文件中都有且仅有一组测试数据。

数据的第一行是一个整数 \(n\) 代表树的节点个数。

第二行有 \(n-1\) 个用空格隔开的整数，第 \(i\) 个整数 \(p_i\) 代表第 \(i+1\) 号节点的家长节点编号。

第三行有 \(n\) 个用空格隔开的整数，第 \(i\) 个整数代表 \(w_i\)。

输出格式

输出一行 \(n\) 个用空格隔开的整数，第 \(i\) 个整数代表想在 \(i\) 号节点上放 \(w_i\) 朵梅花需要准备的梅花个数。

输入输出样例 #1

输入 #1

3 
1 2 
1 1 1

输出 #1

2 2 1

输入输出样例 #2

输入 #2

3
1 1
1 1 1

输出 #2

3 1 1

输入输出样例 #3

输入 #3

6
1 1 2 3 4
3 14 1 5 12 15

输出 #3

21 20 13 20 12 15

说明/提示

输入输出样例 1 解释

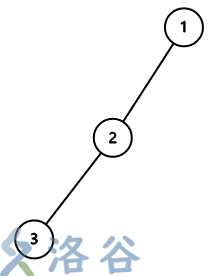
样例 1 的输入如上图，每个节点都需要放一朵梅花。

如果在 1 号节点放梅花，则从 1 号点运动到 2 号点，然后运动到 3 号点，在 3 号点上放一朵梅花，返回 2 号点，在 2 号点上放一朵梅花，同时收回 3 号点的梅花，然后返回 1 号点，将从 3 号点收回的梅花放到 1 号点即可。一共需要两朵梅花。

在 2、3 号节点放梅花的方案类似。

输入输出样例 3 解释

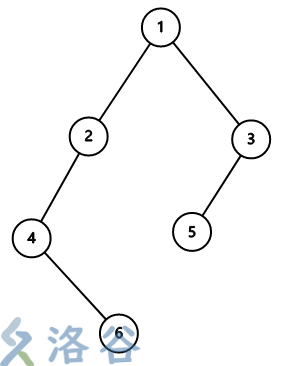
样例 3 的输入如左图。

先从 1 号节点运动至 3 号节点，再运动至 5 号节点，在 5 号节点上放置 \(12\) 朵梅花，然后返回 3 号节点，在 3 号节点上放置 \(1\) 朵梅花，收回五号节点的 \(12\) 朵梅花，返回 1 号节点。

然后运动到 2 号节点，通过 4 号节点运动到 6 号节点，放下 \(15\) 朵梅花，返回 4 号节点放下 \(5\) 朵梅花，此时树上有的梅花数为 \(5 + 15 + 1 = 21\)，分别在 4 号、6 号和 3 号节点上。然后收回 6 号节点的梅花，返回 2 号节点，放下 \(14\) 朵梅花，收回 4 号节点的，返回 1 号节点，在 1 号节点上放置 \(3\) 朵梅花，即可达到在 1 号节点上放梅花的目的。

可以验证最小花费为 \(21\)。其他节点的答案同理。

请注意，其他节点的答案不一定是按照该节点的运动路径行走得到的。

---

数据规模与约定

测试点编号	$n = $	测试点编号	$n = $
1	\(1\)	11	\(100003\)
2	\(8\)	12	\(100003\)
3	\(8\)	13	\(100003\)
4	\(8\)	14	\(100003\)
5	\(8\)	15	\(100004\)
6	\(100000\)	16	\(100004\)
7	\(100000\)	17	\(100004\)
8	\(100002\)	18	\(100004\)
9	\(100002\)	19	\(100004\)
10	\(100002\)	20	\(100004\)

• 对于测试点 5、6，满足特殊性质：每个节点的孩子结点个数不超过 \(2\)。
• 对于测试点 8 到测试点 10，满足特殊性质：每个节点的孩子节点个数不超过 \(5\)。
• 对于测试点 11 到测试点 14，满足特殊性质：任意一个节点到根的路径上的点数不超过 \(3\)，也即树高不超过 \(3\)。
• 对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 10^5 + 4,~1 \leq p_i \leq i,~1 \leq w_i \leq 1000\)。

---

提示

• \(n\) 的末位数字可以帮助你快速的判断测试点所具有的的特殊性质。

题解

记在 \(i\) 节点放置梅花的最小花费为 \(dp_i\) ，\(i\) 节点的权值为 \(w_i\) 。因为

\[dp_u=\max\{ \max_{v\in sons(u)}\{ dp_v + \sum_{k\in sons(u)\ \bigcap\ k\ before\ v}w_k \},\ \ w_u + \sum_{v\in sons(u)} w_v \} \]

我们要求出最优的一种排列使得该式的值最小：

• 对于节点 \(u\) 假设他有两个按顺序的孩子节点 \(v_1,v_2\)。
• 不交换顺序时(即 \(v_1\ ->v_2\))：\(dp_u = \max\{dp_{v_1}, \ dp_{v_2} + w_{v_1} \}\)
• 交换后(即 \(v_2\ ->v_1\))：\(dp_u = \max\{dp_{v_2}, \ dp_{v_1} + w_{v_2} \}\)
• 前者更优则有：\(\max\{dp_{v_1}, \ dp_{v_2} + w_{v_1} \}\le dp_u = \max\{dp_{v_2}, \ dp_{v_1} + w_{v_2} \}\)
  • 若左侧取 \(dp_{v_2} + w_{v_1}\) 则右侧必须取 $dp_{v_1} + w_{v_2} $ 才能满足条件，可以推出 \(dp_{v_1}-w_{v_1}\ge dp_{v_2}-w_{v_2}\)。
  • 假设左侧取 \(dp_{v_1}\) ，因为 \(dp_{v_1} + w_{v_2} > dp_{v_1}\) ，所以无论右侧如何取值该式均成立。
• 综上，贪心排序的策略为：将 \(dp_{i}-w_{i}\) 大的排在前面。时间复杂度为 \(O(n\log n)\)。

点击查看AC代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 5;

int n, w[N], dp[N];
vector<int> g[N];

bool cmp(int a, int b){
    return dp[a] - w[a] > dp[b] - w[b];
}

void dfs(int x){
	dp[x] = w[x];
	for (int i = 0; i < g[x].size(); i++){
		dfs(g[x][i]); 
        dp[x] += w[g[x][i]]; // 所有w相加
    }
    sort(g[x].begin(), g[x].end(), cmp);   // 排序出儿子节点遍历顺序 
    int sum = 0;
	for (int i = 0; i < g[x].size(); i++){   // 即按顺序放花时中间的最大值要考虑
        dp[x] = max(dp[x], dp[g[x][i]] + sum);
        sum += w[g[x][i]];
    }
}

void solve(){
    cin >> n;
    for(int i = 2; i <= n; i++){
        int p; cin >> p;
        g[p].emplace_back(i);
    }
    for(int i = 1; i <= n; i++) cin >> w[i];

    dfs(1);
    for(int i = 1; i <= n; i++) 
        cout << dp[i] << " \n"[i==n];
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    solve();
    return 0;
}