背包九讲学习笔记
2019-09-30
用了两天把背包九讲看完了,学习笔记如下,不确之处欢迎指正
一、一切背包的基础——01背包
将 $ N $ 件物品放入容量为 $ V $ 的背包,第 $ i $ 件物品的体积(也就是花费)是 $ C_i $ ,价值是 $ W_i $,且每个物品只有一个,求可以达到的最大价值。
定义 $ F ( i, v ) $ 为用第 $1$ 到第 $ i $ 件物品来装一个容量为 $ v $ 的背包可以得到的最大价值,则对于第 $ i $ 件物品,有状态转移方程:
$ F(i, v)=\max\limits_{C_{i}<v\leqslant V}\{F(i-1, v), F(i-1,v-C_i)+W_i\} $
如果放弃第 $ i $ 件物品就取第一项,也就是说和用第 $ 1 $ 到第 $ i-1 $ 件物品来装一个容量为 $ v $ 的背包的问题没什么两样;如果要放入第 $ i $ 件物品则取第二项,获得$ W_i $ 价值的同时体积也得减少$ C_i $ ,留下子问题变为用第 $ 1 $ 到第 $ i-1 $ 件物品来装一个容量为 $ v-C_i $ 的背包。
for (int i = 1; i <= N; i++)
for (int v = C[i]; v <= V; v++)
F[i][v] = max(F[i - 1][v], F[i - 1][v - C[i]] + W[i]);
时间复杂度为$ O(NV) $
空间复杂度优化:注意到每次状态转移都只涉及到F的第$ i $和第$ i-1 $项,所以可以把下标$i$去掉,把F降维成$F[v]$。但是应该看到:在第$i$轮循环里,算原$F[i][v]$要用到$F[i-1][v-C_i]$, 就是说不能还从比较小的v更新,否则算$F[v]$用的就是这一轮的原$F[i][v-C_i]$了。代码:
for (int i = 1; i <= N; i++)
for (int v = V; v >= C[i]; v--)
F[v] = max(F[v], F[v - C[i]] + W[i]);
这里可以把一次计算看成一个函数(即抽象过程),它的功能是对于每一个背包容量$v$,确定选不选第$i$件物品,$F[v]$是对应最优值。
void ZeroOnePack (int F[], int C, int W)
{
for (int v = V; v >= C; v--)
F[v] = max(F[v], F[v - C] + W);
}
初始化:$\Big\{^{F[0] = 0}_{ \forall i \in \{1, 2, ..., N\}, F[i] = -\infty}$对应恰好装满背包问题,而 $ \forall i \in \{0, 1, 2, ..., N\}, F[i] = 0$对应不必须把背包装满,只是求价值最大。
一种想法是初始化时,F就是没东西可以放进去的合法状态。因为递推式里面取max,所以设成$-\infty$。但应该注意到这里面的负无穷是真的无穷,加上任何数还是负无穷。这样写代码不方便,不如设成-1然后在写循环的时候作特殊处理。
常数级优化:这一点因为原文有错而且网上众说纷纭,想了好长时间才完全弄对。
正确的下限应该是$\max\{V-\sum^{N}_{j=i+1}C_j, C_i\}$。
有人还认为下标是从$i$开始,也有人对此的解释太感性了,说剩下的可以全装下就不要管了。我画了一个表,把问题想清楚了:
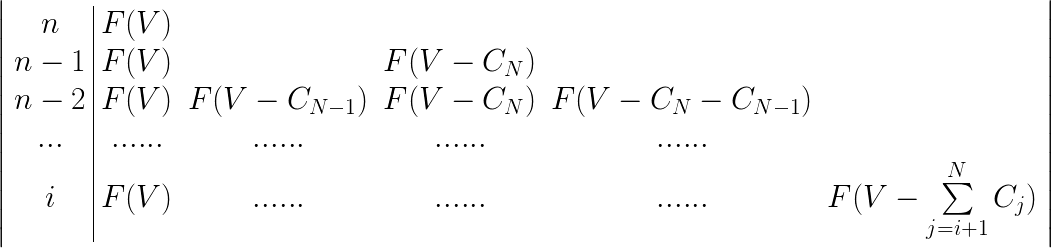
也就是说, 我们只要求$F(V)$的话,就不用管$V-\sum^{N}_{j=i+1}C_j$之后的,因为它们对$F(V)$是一定没有影响的。
考虑到另一个下限,综合来看的常数优化应该是到$\max\{V-\sum^{N}_{j=i+1}C_j, C_i\}$,当背包体积特别大时还是可以优化不少的。
二、“简单”的背包——完全背包
将 $ N $ 件物品放入容量为 $ V $ 的背包,第 $ i $ 件物品的体积(也就是花费)是 $ C_i $ ,价值是 $ W_i $,每个物品可以无限取,求可以达到的最大价值。
第一眼看上去的做法就是把每个物品变成价值相同的$ V/C_i $件物品,然后再跑01背包,状态转移方程为:
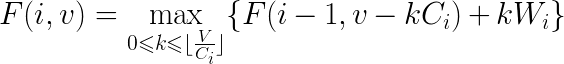
但是,这样时间复杂度为$O(NV\sum{V\over {C_i}})$,代价太大。
一个简单的优化是先贪心,只保留费用相同的物品中价值最高的那一个而剩下的不管,具体实现上可以仿照计数排序,先开一个下标和费用相关的数组,然后每个费用对应的数组值为价值最大的那个物品的下标,最后只看剩下的那些下标来计算。
也可以用二进制拆分来简化复杂度,但是有一个更简单而且复杂度更低的办法,就是在01背包上稍作改动:
for (int i = 1; i <= N; i++)
for (int v = C[i]; v <= V; v++)
F[v] = max(F[v], F[v-C[i]]+W[i]);
这个算法是$O(VN)$的,和01背包的一维形式只有循环次序上的不同。
为什么这样可以凑效呢?可以这样想:当时我们要倒过来正是因为要避免和这一轮的$F[i][v-C_i]$有联系,如今装了第$i$个物品我们还能再装一个第$i$个物品进去,所以要考虑到之前可能已经装了$i$在里面的情况,必须递增循环。并且因为物品可以无限取,每次循环相当于只有背包容量可能变化,面对的子问题选物品都一样,所以也可以对于不同背包容量考虑每一个物品,所以循环次序可以颠倒,可能有常数上的优化。
也可以抽象出来函数,表示对每一个背包容量考虑放体积为$C$、价值为$V$的物品值不值:
void CompletePack (int F[], int C, int W)
{
for (int v = C; v <= V; v++)
F[v] = max(F[v], F[v - C] + W);
}
三、二进制或单调队列优化——多重背包
与完全背包的第一个方程类似,只是每个 $k$ 有范围:
$ F(i,v)=\max\limits_{0\leqslant k\leqslant M_i}\{F(i-1,v-kC_i)+kW_i\}$
但这样全看成一个一个的独立物品来跑01背包的时间复杂度是$O(V \sum M_i)$,$M_i$比较大时会超时。
可以用二进制改进:用$1,2,2^2,...,2^{k-1},M_i-2^k+1$,其中$k$要使最后一项大于0。
和一个纯$2$的幂构成的基底,最后一项取成$M_i-2^k+1$有什么好处呢?第一,这样确实可以用更少的数来表示出小与$M_i$的所有正整数;第二,他们全相加和为$M_i$,避免以后还要处理基底相加结果大于$M_i$的情况。这样再来跑01背包,时间复杂度可以优化为$O(V \sum logM_i)$。
同样,把这个过程抽象出来,对每一个$v$确定对于$M$个价值为$W$,体积为$C$的物品的选择策略:
void MultiplePack(int F[], int C, int W, int M)
{
if (C * M >= V) //如果物品太多了,直接当成完全背包
{
CompletePack(F, C, W);
return;
}
int k = 1;
while (k < M) //这里用到了一个技巧
{
ZeroOnePack(F, k * C, k * W);
M -= k; //M最后会取到最后一个基底
k = 2 * k;
}
ZeroOnePack(F, C * M, W * M);//对最后一个基底来考虑
}
用01背包来处理的原因是,他们
因为倒数第二个数只取到$2^{k-1}$,而最后一轮为第$n$轮,$M$已经缩小到了$M-(1+2+2^2+...+2^{n-1})=M-2^n+1$,$k$为$2^{n-1}$,循环结束后再把$M-2^n+1$处理一下即可。
一个稍微有点复杂的办法是传说中的单调队列优化,可以均摊$O(1)$时间内就求出$F(i,v)$,从而用$O(NV)$的时间复杂度求解。
其实它的思想很简单:可以想象手在一根写满数字的长纸条上滑动,要求手所覆盖的那一段纸带上的最大数字。
我们可以构造一个队列,先开始只有第一个数字,每次滑动如果队首不在手里面,就要出列;每次从后面再加进去一个数字,这个数字要把队列里面不大于它的所有数字全挤掉。这样,每次只要取队首即为这段区间上的最大数字。
这样,取队首要$O(1)$时间,维护队首和新进队元素也要$O(1)$时间,总的来说均摊$O(1)$可以求解。
这和多重背包问题有什么联系呢?我们站在带余除法的观点上,再来看一下原递推方程:
设$v=qC_i+r$
则$ F(i,v)=\max\limits_{0\leqslant k\leqslant M_i}\{F(i-1,v-kC_i)+kW_i\}=\max\limits_{0\leqslant k\leqslant M_i}\{F(i-1,(q-k)C_i+r)+kW_i\}$
设$m=q-k$
有$F(i,v)=\max\limits_{q-M_i\leqslant m\leqslant q}\{F(i-1,mC_i+r)-mW_i\}+qW_i$
降维成滚动数组的话,还可以这样看:
$F(v)=F(qC_i+r)=\max\limits_{q-M_i\leqslant m\leqslant q}\{F(mC_i+r)-mW_i\}+qW_i$
单调队列负责解决的就是上一轮那$M_i$个$F(mC_i+r)-mW_i$的最大值。
到了这一步,就直接把$v$给抛弃掉了,先遍历$v \equiv r ( mod \ c_i) $当中的余数$r$(即遍历剩余类),再遍历$q$。
注意到$k\leqslant q$,也就是说只要维护$q$和之前的$M_i$个数的单调队列。
void HumdrumQueueMultiPack(int F[], int C, int W, int M)
{
if (V / C < M)
M = V / C;// 确定最大可取物品数目
struct
{
int Pos;
int Value;
}que[M+5];
int head = 0,tail = 0;// head队首,tail超尾
for (int r = 0; r < C; r++)// 余数
{
head = tail = 0;
for (int q = 0; q <= (V - r) / C; q++)// 上限的来历:v = q*C+r <= V
{
int x = q;// 设x和y是为了方便
int y = F[q * C + r] - q * W;
// 单调队列维护
// 先看队首是不是要出队,再看新加进来的要淘汰几个之前的老元素
// 解析中的m不会出现
while (head < tail && que[head].Pos < q - M)
head++;
while (head < tail && que[tail - 1].Value <= y)
tail--;
que[tail].Value = y;
que[tail].Pos = x;
tail++;
// 加上那个常数
F[q * C + r] = que[head].Value + q * W;
}
}
}
for (int i=0; i<N; i++)
HumdrumQueueMultiPack(F, C[i], W[i], M[i]);
如此,总时间复杂度为$O(NC_i{V \over {C_i}})=O(NV)$,每个$F(i,v)$均摊$O(1)$。
如果算法只要求是否可以填满背包,即不考虑价值的话,还有一种比较直观$O(NV)$的做法。
我们更改$ F(i,v) $的定义,让其等于“用前$i$种物品填满容量为$v$的背包以后,最多还剩下几个第$i$种物品”。但要注意:有可能填不满背包,所以有些状态无解,取成$-1$;其他状态下$F(i,v)\in [0,M_i]$。
// 总初始化
F[0][0] = 0;// 只有容量为0的背包才能在无物品可用的情况下装满,此时剩下0个物品
for (int i = 1; i <= V; i++)
F[0][i] = -1;
for (int i = 1; i <= N; i++)
{
// 动态规划初始化
for (int v = 0; v <= V; v++)
if (F[i-1][v] >= 0)
F[i][v] = M[i];// 用第1~i-1个物品就能填满,不需要i,第i个物品剩下M[i]个
else
F[i][v] = -1; // 否则,先认为它不可能,设其为-1
// 动态规划
for (int v = 0; v <= V-C[i]; v++)// 必须从小到大
if (F[i][v] > 0) // 如果用前i个物品装容量为v的背包有剩下的,那么可以用来装j+C[i]背包
F[i][v+C[i]] = max(F[i][v+C[i]], F[i][v]);
}
可以这样来理解:在动态规划初始化部分,$F(i,v)$中有一部分从$F(i-1,0...V)$中继承了家产,剩下的则全是赤贫的“负产阶级”。而在动态规划部分,“继承者们”要先富带后富,“负产阶级”当中有一部分或者全部就也获得了财富;当有多个继承者给予同一个“负产者”时,只留下最多的那一个。
四、前面三种背包的混合
如果只是01背包和完全背包的结合,那很容易,只要改变循环顺序即可;如果三者兼有,也不是特别麻烦。这里就体现出抽象的威力了:
//约定物品属于01背包时 Id[i]=1,属于完全背包时 Id[i]=2,属于多重背包时 Id[i]=3。
for (int i=1, i<=N, i++)
{
if (Id[i]==1)
ZeroOnePack(F, C[i], W[i]);
else if (Id[i]==2)
CompletePack(F, C[i], W[i]);
else
MultiplePack(F, C[i], W[i], M[i]);
}
五、升维——二维背包
现在考虑一个物品有两种花销,比如它的体积和装进背包所需的力气。正如背包的体积是有限的一样,一个人的力气也是有限的。求这种情况下可以获得的最大价值。
实际上,有一类NP难问题就是$MDKP (multidimensional knapsack problem)$,这方面的新算法研究层出不穷。但对于二维背包,我们只要简单地加一个维度即可。
状态转移方程:$ F(i, v, u)=\max\{F(i-1, v, u), F(i-1,v-C_i, u-D_i)+W_i\} $
同样,空间复杂度可以优化到$O(N^2)$,把$i$给去掉。如果都是01背包则对$u$和$v$都逆序;如果都是完全背包则全升序(代码如下);如果$u$是01背包而$v$是完全背包则对应逆顺序。
for (int i = 1; i <= N; i++)
for (int v = C[i]; v <= V; v++)
for (int u = D[i]; u <= U; u++)
F[v][u] = max(F[v][u], F[v-C[i]][u-D[i]]+W[i]);
还有一种隐含的二维背包是物品总个数有限制:比如说最多取到$L$件物品。这个时候可以考虑每个物品还有件数花销$1$,总共不能超过$L$。
六、简单但有深意——分组背包
在01背包的基础上,又已知所有物品被分为$K$组,每组里面最多选一个。
就这一题而言,一个直观的算法是:
for (int k = 1; k <= K; k++)
for (int v = V; v >=0; v--)
for (每一个在第k组里面的物品i)
F[v] = max(F[v], F[v-C[i]]+W[i]);
可以先进行贪心优化,见第二节。
深意在于,它告诉我们:可以将一堆物品看成一个组来求解,前提是这些物品互相冲突。第七节就是一个例子。
七、泛化的开始——元素间有依赖的背包
如果装包包的时候装有些物品之前必须先装另一些物品怎么办呢?比如说,想在宾馆里面健身先要有房卡,但是有房卡的可以不去再花钱跑到宾馆的健身房锻炼。
简化的问题是,“附件”只能有一个“主件”,也没有附件的附件。
直接做的话,因为一个主件的$n$个附件对应了$2^n+1$种取法,指数级会超时。
但是想一想这些策略都是互相冲突的,可以先贪心只留下费用相同的策略中价值最大的那一个。具体是:
先假设装上这个主件$i$,对它的附件跑容积为$V-C_i$的01背包,确定对于容积从$0$到$V-C_i$的最优策略,其中总费用为$C_i+v$的物品价值为$F(i,v)+W_i$,然后直接用第六节的算法解题即可。
设有$k$个主件,$N-k$个附件,第$i$个主件有$Num_i$个附件
则时间复杂度为$O(\sum\limits_{i=1}^k ({Num_i(V-C_i)+V(V-C_i+1)})=O(kV^2+NV-V\sum\limits_{i=1}^k C_i(Num_i+1))$
最坏情况下,每个主件花费为$1$,时间复杂度为$\Omega (kV^2+NV-V-N+k)=\Omega (kV^2+NV)$。
如果附件还可以再有附件,则可以把整个物品组看成一个树,进行树形动态规划,即求父节点时先要把所有子节点的最大价值求出来。但实际上,可以用泛化物品的概念来避免建树
八、函数式思维的威力——泛化物品
泛化物品建就是把价值看成费用的一个函数。
对01背包,它是单点函数$h(C_i)=W_i;
对完全背包,它是$h(x)=W_i {\frac {x}{C_i}}, C_i|x$;
对多重背包,它是$h(x)=W_i {\frac {x}{C_i}}, C_i|x$且${{x}\over{C_i}}\leqslant M_i$;
对分组和有依赖的背包,一个物品组看成一个物品,它是对所有的$v$不同策略可以取到的最大价值。
总之,不论有何种分组和依赖关系,都可以看成函数,也就是泛化物品。
两个泛化物品的和函数为:$f(c)=\max\limits_{0 \leqslant k \leqslant v} {h(k)+l(v-k)}$。这样一直合并下去直到只有一个函数$Final(v)$,$Final(V)$就是答案。
这样做,时间复杂度为$O(V^2)$。
PS:背包九讲作者看的可能是SICP,从而发现了这种办法。
九、背包相关
要输出方案的话,就不可以进行空间优化了。
int v = V; for (int i=N; i>0; i--) { if (F[i][v]==F[i-1][v]) printf("0");// 未选 else { printf("1");// 已选 v-=C[i]; } }
输出字典序最小的方案时,可以反过来循环然后再用上面的代码展示:
for (int i = N; i > 0; i--)
for (int v = V; v >= C[i]; v--)
F[i][v] = max(F[i + 1][v], F[i + 1][v - C[i]] + W[i]);
求装满背包或者将背包装至某一容量的方案总数的话,可以直接改$F(i,v)$的定义:用前$i$个物品装到$v$的方案数:
for (int i = 1; i <= N; i++)
for (int v = C[i]; v <= V; v++)
F[i][v] = F[i - 1][v]+ F[i][v - C[i]];
如果求最优方案总数,可以再定义一个数组$G(i,v)$表示用前$i$个物品装到$v$的最优方案数:
for (int i = 1; i <= N; i++)
G[i][0] = 1;
for (int i = 1; i <= N; i++)
for (int v = C[i]; v <= V; v++)
{
F[i][v] = max(F[i - 1][v], F[i - 1][v - C[i]] + W[i]);
G[i][v] = 0;
if (F[i][v] == F[i - 1][v])
G[i][v] += G[i - 1][v];
else
G[i][v] += G[i - 1][v - C[i]];
}
求次优解、第$K$优解,复杂度要乘以$K$,可以升一维,合并的时候有点像归并排序里面的$Merge$过程,取两个数组中最大的$K$个数形成新的数组:
for (int k=0; k<=K; k++)
F[i-1][v-C[i]][k] += W[i];
Merge(F[i-1][v], F[i-1][v-C[i]], F[i][v]);
要注意策略不同但权值相同的两 个方案是看作同一个解还是不同的解。如果是同一个解,则要保证队列里面没有重复的。
十、真实背包——体积为实数的01背包
注意到$F(i,v)$当中$v$为实数时是连续变量,没办法再用二维数组来解。但是递归式是成立的,而且因为每次都取max,$i$固定时$F(i,v)$是$v$的单调不减阶梯状函数。
可以用一个$p[i]$存储$i$所有的跳跃点$(v,F(i,v))$,由递推式注意到$p[i]$其实可以从$p[i-1]$生成:
十一、背包展望
除了动态规划以外,其实还有一些演化近似算法,有些非强NP难问题甚至还有完全多项式时间近似方案(fully polynomial time approximation scheme, FPTAS)。但是因为这已经超出了ACM竞赛的范围,而且有时候还不能求得全局最优解,就不细说了。关键是,虽然已经可以解决很多不同的背包问题,我们也不能因此得意起来,要想在多项式时间内解决它们,目前看来还遥遥无期——这正是现代算法研究的一个前沿课题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号