决策单调性优化 DP
前言
为了一道题目,前前后后大约搞了三个小时,当然还是没有看懂,为了巩固知识,遂出此笔记。
定义
决策单调性
在转移方程 \(dp[i]=\min/\max\{dp[j]+w(i,j)\}(1\le j< i)\) 中,其中 \(L_i\) 与 \(R_i\) 单调递增,若函数 \(w()\) 满足四边形不等式,则 \(dp[]\) 具有决策单调性。
四边形不等式
\(w(x, y)\) 为定义在整数集合上的一个二元函数,若 \(\forall a \leq b \leq c \leq d,\; w(a,c) + w(b,d) \leq w(a,d) + w(b,c)\),那么函数 \(w\) 满足四边形不等式。
为什么叫做四边形不等式呢?在 \(w(x,y)\) 函数的二维矩阵中挖一块四边形,左上角加右下角小于等于左下角加右上角。
定理
四边形不等式
\(w(x, y)\) 为定义在整数集合上的一个二元函数,若 \(\forall a < b,\; w(a,b) + w(a+1,b+1) \le w(a+1,b) + w(a,b+1)\),那么函数 \(w\) 满足四边形不等式。
证明:
上下两式相加,有:
以此类推 \(\forall a \le b \le c,\; w(a,c) + w(b,c+1) \le w(a,c+1) + w(b,c)\)
同理 \(\forall a \le b \le c \le d,\; w(a,c) + w(b,d) \le w(a,d) + w(b,c)\)
决策单调性
在转移方程 \(f[i] = \min/\max\left\{f[j] + w(j,i)\right\},\; j \in [0,i)\)(为方便描述,以下都使用 \(\min\) 作正,\(\max\) 同理) 中,若函数 \(w\) 满足四边形不等式,则 \(f\) 具有决策单调性。
定义 \(p[i]\) 表示 \(i\) 的最优决策点。
根据 \(p[i]\) 为 \(i\) 的最优决策点,则有
因为 \(w\) 满足四边形不等式,则有
移项,可得
与第一个不等式相加,可得
即 \(i'\) 的最优决策点一定大于等于 \(p[i]\)。故 \(dp[]\) 具有决策单调性。
应用
那么知道其有决策单调性后,有什么应用呢?
既然其有决策单调性,定义 \(p[i]\) 表示 \(i\) 的最优决策点,则 \(p\) 内一定是非严格单调递增的。
那么根据此性质,满足决策单调性的题目主要有两种处理手法。
方法一:单调队列
用单调队列维护单调的决策点,二分找到最优决策点。
以 P3515 Lightning Conductor 为例。
题目大意:在给定长度为 \(n\) 的序列 \(a\) 中,对于每一个 \(i\),找到最小的自然数 \(p_i\) 满足对于任意的 \(j \in [1,n]\),均有
把这个式子变形:
即
也可以拆分为:
可以发现里面两个 \(\max\) 可以视为同一个问题(只要把序列翻转一下就可以了),所以只需要考虑求出对于每一个 \(i\) 的 \(\max_{j \in [1,i]}\left\{a_j + \sqrt{i-j}\right\}\)。
设
那么我们会得到 \(n\) 个关于 \(i\) 的函数,且
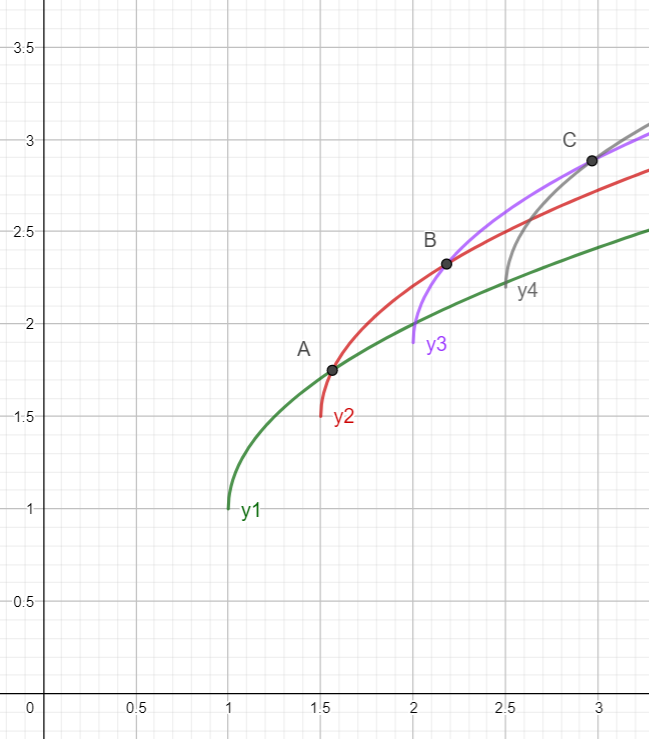
将样例画出来,如图:
可知当 \(i=4\) 时,直线 \(x=4\) 与 \(y_1 = a_1 + \sqrt{x-1}\) 的交点即为 \(p_4\)。
在上图中,对于任意 \(j \in [1,n]\),\(y_1\) 总是在最上面,也就是说下面的其他函数可以踢掉不要,但由于 \(\text{sqrt}\) 函数的增速递减,会出现如图中 \(y_2,y_4\) 的情况,即存在一个交点使得在该点两边两条直线的位置关系不同。此时如果没有上面的 \(y_1\),\(y_2,y_4\) 都有可能成为答案,所以不能乱踢。
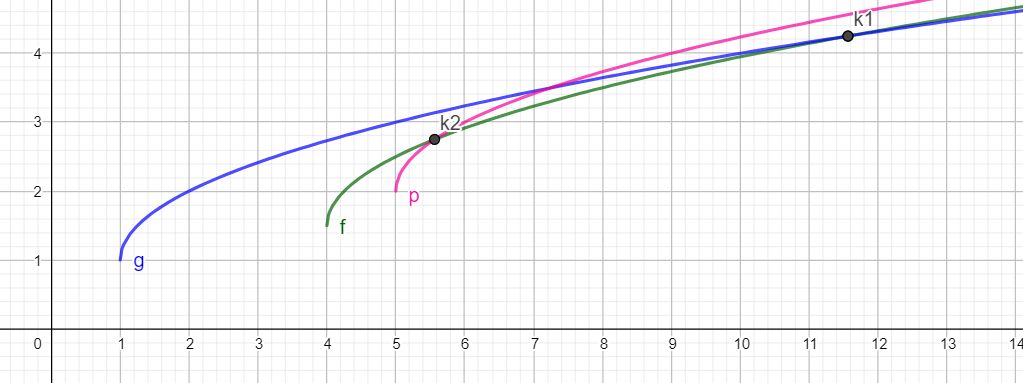
看下面这种情况:
设 \(k_1\) 为 \(y_1,y_2\) 的交点,\(k_2\) 为 \(y_2,y_3\) 的交点。
此时 \(k_1 > k_2\),可以发现 \(y_2\) 始终在其他直线的下面,可以放心的将其踢掉。
所以维护出来的决策集合大概就是酱紫的:
对于不同的 \(i\) 来说,都有一个互不不同的直线在最上方,所以该决策集合里的直线都是有用的。可以从图中看出,最优决策点单调递增。
维护决策集合用单调队列,查找直线交点用二分,随便搞搞就行了。
方法二:分治
假设已知 \([l, r]\) 的最优决策在 \([L, R]\) 上。
定义 \(mid = \frac{l+r}{2}\),设 \(dp[mid]\) 的最优决策为 \(p\),根据决策单调性,可知 \([l, mid-1]\) 的最优决策在 \([L, p]\) 内,\([mid+1, r]\) 的最优决策在 \([p, R]\) 内。
于是将问题分割成了同类型的规模更小的问题,便可递归分治。
复杂度均为 \(O(n\log n)\)。
代码实现
方法一:单调队列
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, a[N];
double dp[N], sqr[N];
int head, tail;
int Q[N], poi[N];
double get(int i, int j) {
return (double)a[j] + sqr[i - j];
}
int Find(int j1, int j2) { // 找到两个直线的交点 i
int l = j2, r = n, mid;
int ans = n + 1;
while (l <= r) {
mid = (l + r) >> 1;
// 当前这个位置 i 使得直线 j1 的纵坐标小于直线 j2 的纵坐标,说明这个点 i 在交点的右方,所以右边界要缩小
if (get(mid, j1) <= get(mid, j2)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return ans;
}
void DP() {
head = 1, tail = 0;
for (int i = 1; i <= n; i++) {
// 满足上图情况:即队尾 y2 彻底没用的情况
while (head < tail && Find(Q[tail], i) <= poi[tail - 1]) --tail;
int cp = Find(Q[tail], i);
poi[tail] = cp, Q[++tail] = i; // 由于 i 本身也是一个决策点,所以要先入队再取答案择优
// 找到第一个位置 j 使得直线 Q[j] 与直线 Q[j + 1] 的交点大于 i,
// 那么直线 Q[j] 就是 i 前面在最上面的直线,即答案
while (head < tail && p[head] <= i) ++head;
dp[i] = max(dp[i], get(i, Q[head]));
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
sqr[i] = sqrt(i);
}
DP();
for (int i = 1; i <= n / 2; i++) {
swap(a[i], a[n - i + 1]);
swap(dp[i], dp[n - i + 1]);
}
DP();
for (int i = n; i >= 1; --i)
cout << (int)ceil(dp[i]) - a[i] << endl;
return 0;
}
方法二:分治
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, a[N];
double dp[N], sqr[N];
double w(int j, int i) {
return double(a[j]) + sqr[i - j];
}
void work(int l, int r, int L, int R) {
if (l > r) return;
int mid = l + r >> 1, p;
double maxn = 0;
for (int i = L; i <= min(mid, R); i++) {
if (w(i, mid) > maxn) {
maxn = w(i, mid);
p = i;
}
}
dp[mid] = max(dp[mid], maxn);
work(l, mid - 1, L, p);
work(mid + 1, r, p, R);
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
sqr[i] = sqrt(i);
}
work(1, n, 1, n);
for (int i = 1; i <= n / 2; i++) {
swap(a[i], a[n - i + 1]);
swap(dp[i], dp[n - i + 1]);
}
work(1, n, 1, n);
for (int i = n; i >= 1; i--) {
cout << (int)ceil(dp[i]) - a[i] << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号