2025年12月09日 模拟赛总结

Treasure Hunt

前面 \(k(x+y)\) 米都不用管，只有判断最后不到 \(x+y\) 米就可以了。

#include <bits/stdc++.h>
using namespace std;

int x, y, a;
void solve() {
    cin >> x >> y >> a;
    
    int lst = a % (x + y);
    if (lst < x) cout << "NO\n";
    else cout << "YES\n";

}

int main() {
    int T;
    cin >> T;

    while (T--) solve();
    return 0;
}

Pushing Balls

如果一个球的左边与上边都没有全部填满，那么就绝对不可能成功，因此用二维前缀和维护就可以了。

#include <bits/stdc++.h>
using namespace std;

int n, m;
int a[55][55];
int pre[55][55];
bool flag;
char c;

int main() {
    int t;
    cin >> t;
    while (t--) {
        flag = false;
        cin >> n >> m;

        // 读取矩阵数据（处理输入中的空白字符）
        for (int i = 1; i <= n; i++) {
            while (c != '0' && c != '1') c = getchar();
            for (int j = 1; j <= m; j++) {
                a[i][j] = c - '0';
                c = getchar();
            }
        }

        // 计算二维前缀和
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                pre[i][j] = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] + a[i][j];
            }
        }

        // 检查每个1的位置是否符合条件
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (a[i][j] == 1) {
                    if (pre[i][j] - pre[i][j - 1] != i && pre[i][j] - pre[i - 1][j] != j) {
                        cout << "NO\n";
                        flag = true;
                        break;
                    }
                }
            }
            if (flag) break;
        }

        if (flag) continue;
        cout << "YES\n";
    }
    return 0;
}

Dining Hall

下图表示到达大厅中的所有桌子（灰色部分）所需的最小步数：

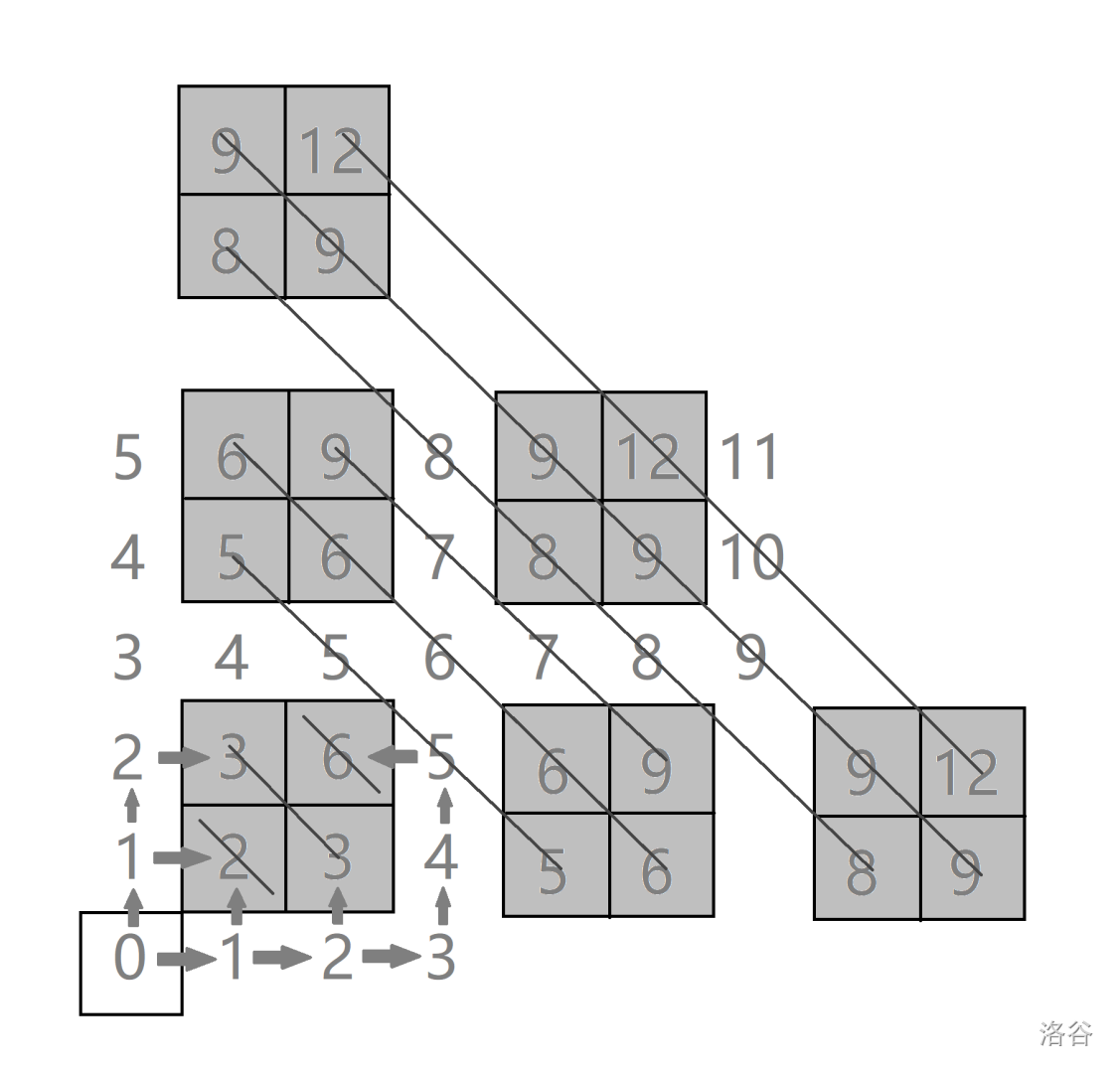
由此可以发现相同步数的位置呈斜向排列，我们可以得到：到达一个桌子上的位置 \((x,y)\) 的步数，等同于到达另一张桌子上的位置 \((x+3,y-3)\) 的步数。

为了找到当前距离最小的点，可以用优先队列维护。为了防止堆空情况，我们还有维护一个目前可能的最优位置，这个位置所在的桌子没有人。

具体如下：

• 如果当前客人需要空位置，我们就去优先队列里找（前提是堆不为空，并且要求队顶距离要小于目前已知并且可以提供的最小距离），那么就把优先队列队顶的元素给予这位客人，并且弹出。
• 如果上述条件没有满足，则把目前可能的最优位置所在桌子的另外三个位置塞入队列，并把目前可能的最优位置给予这位客人，然后更新可能的最优位置。

#include <bits/stdc++.h>
#define ll long long
using namespace std;

struct node {
    int dis, x, y;
    bool operator<(const node t) const {
        if (dis != t.dis) return dis > t.dis;
        if (x != t.x) return x > t.x;
        if (y != t.y) return y > t.y;
    }
};

ll T, n;

int main() {
    cin >> T;
    while (T--) {
        priority_queue<node> pq;
        ll x = 1, y = 1, now = 2;
        cin >> n;
        
        vector<pair<ll, ll>> ans(n + 1);
        
        for (ll i = 1, xx; i <= n; i++) {
            cin >> xx;
            
            if (xx && !pq.empty() && pq.top().dis < now) {
                auto p = pq.top();
                pq.pop();
                ans[i] = { p.x, p.y };
            } else {
                ans[i] = { x, y };
                
                pq.push({x + y + 1, x + 1, y});
                pq.push({x + y + 1, x, y + 1});
                pq.push({x + y + 4, x + 1, y + 1});
                
                if (y - 1) x += 3, y -= 3;
                else swap(x, y), y += 3;
                
                now = x + y;
            }
        }
        
        for (ll i = 1; i <= n; i++)
            cout << ans[i].first << " " << ans[i].second << endl;
    }
    return 0;
}