【学习笔记】线段树合并
前言
线段树合并是指对于多棵区间相同的线段树，将他们的信息合并到一棵线段树上。
每次合并两棵，合并的结果就附在其中一棵线段树上。
看起来挺神秘的，其实也不难。
前置知识
权值线段树
我们知道线段树维护的是区间上的信息，如最大值、最小值、区间和等信息。它维护的对象是数组，一般情况下，线段树维护的区间是数组下标对应的区间。
而权值线段树是指以值域为区间建立的线段树，它维护的区间是一段值域。所以称为权值线段树。
动态开点线段树
因为维护的是值域，而值域可能范围很大，且值域中许多位置是空的，没有对应的元素。我们只需要将存在的元素插入到线段树中即可。
此时，叶节点的数量就是有效的元素值的数量。每个叶节点的祖先最多 \(\log m\) 个，这棵线段树的节点数量也不超过 \(n\log m\)。其中 \(n\) 是元素个数，\(m\) 是值域大小。
当然，如果在此基础上使用离散化优化的话，常数可以变得小一些，即结点数量会从 \(n\log m\) 降到 \(n\log n\)。
动态开点线段树已经不符合完全二叉树的性质了，所以，不能再用 \(i\times 2\) 表示 \(i\) 的左儿子，\(i\times 2 + 1\) 表示 \(i\) 的右儿子了。
因此我们需要对每个结点另存两个变量：每个结点的左儿子和右儿子。
struct node {
int l, r, lc, rc, cnt;
// l, r 表示当前结点控制的区间 [l, r]
// lc, rc 表示当前结点的左儿子与右儿子
// cnt 表示当前结点的出现次数
};
那么到底应该如何去理解这个过程呢？下面这个例子或许可以帮到你。
给定一个 \(n\)，请画出 \(1\sim 1,1\sim 2,1\sim 3,...,1\sim n\) 的线段树。
为方便理解，这里我们假设 \(n=4\)。
那么我们将会画出下面的图：
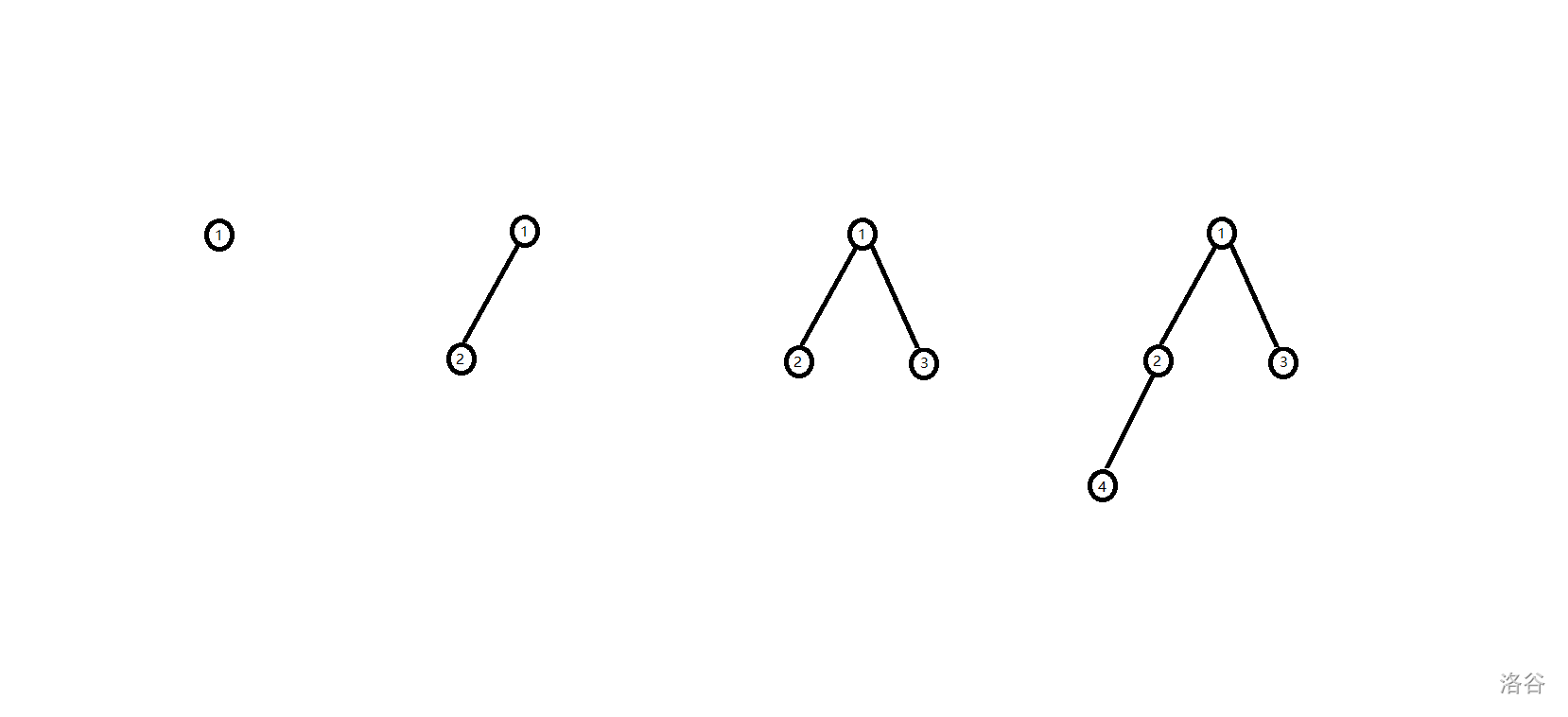
这里我们需要使用的结点其实只有 \(4\) 个，但是我们却耗费了 \(10\) 个结点的空间，非常浪费。
因此我们可以考虑在建立前一棵线段树的基础上再多加一条链，这样就可以避免空间的极度浪费了。
如图，这样就可以节省很多空间了：
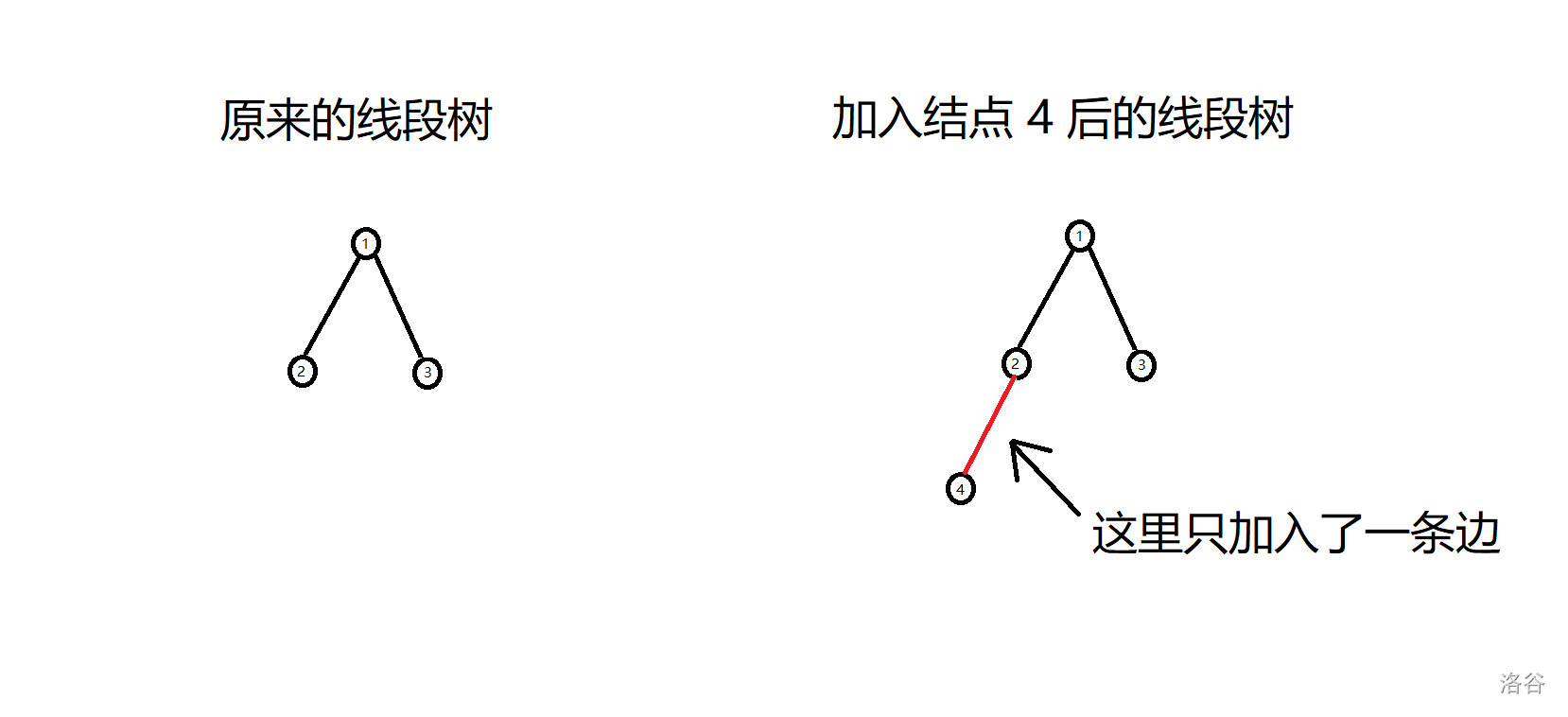
线段树合并
一般情况
考虑将两棵线段树合并，具体而言，如下：
- 如果两颗线段树都有共同的一个结点，那么将两颗线段树在这个结点上的信息进行合并
- 如果两颗线段树中只有一棵线段树有一个结点，而另一个线段树没有，那么就将新的线段树连向这个结点
举个例子，这里的合并就用权值相加来理解：
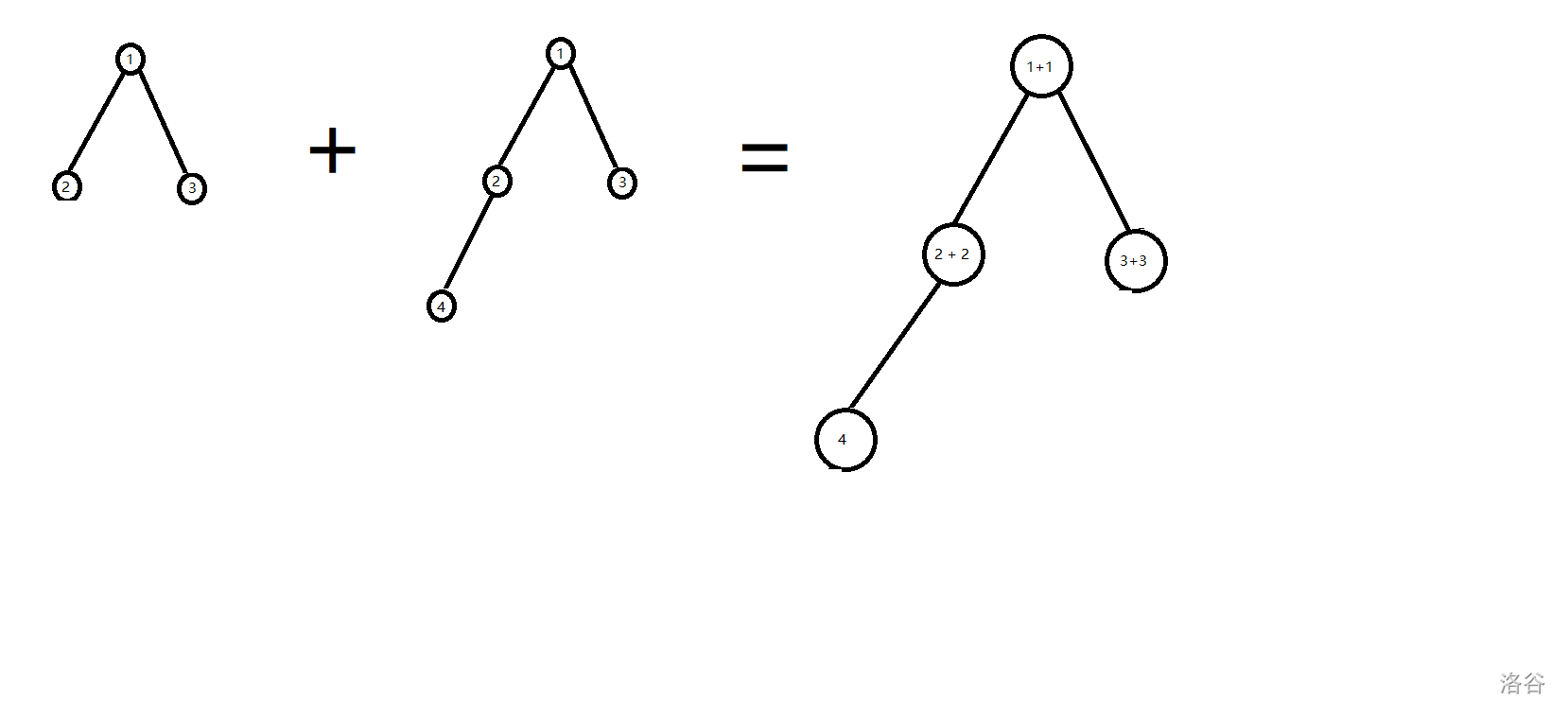
复杂度分析
将两个线段树合并时，遇到空节点直接返回，也就是只有两个线段树的重合部分会被 Dfs 到。所以总的合并次数不会超过较小的线段树的节点数。即单次合并复杂度不会超过 \(O(n\log n)\)。
如果进行了很多次合并，那么时间复杂度依然是 \(O(n\log n)\)，原因是如果将两个线段树合并，事实上不会增加新的节点，而较小的线段树永远的消失了，也就是对于每一棵线段树，在合并一次后，要么对方消失，要么自己消失。即所有的节点都只会被合并一次。那么无论合并多少次，总的时间复杂度就是 \(O(n\log n)\)。
由上可知，空间复杂度也为 \(O(n\log n)\)，不过具体大小随题目的变换会有常数上的变动。
树上合并
和一般情况其实并没有什么区别。用树上前缀和的思想，将一个节点所有儿子对应的线段树合并，然后再和它自身合并即可。
相关例题
P4556 【模板】线段树合并
对于每一个节点，开一颗权值线段树，维护值域最大值。修改时利用树上差分进行修改。然后进行树上前缀和合并即可。
时空复杂度 \(O(n\log n)\)，注意空间有四倍的常数。
#include <bits/stdc++.h>
#define ll long long
#define lson tree[id].ls
#define rson tree[id].rs
#define mid ((l + r) / 2)
using namespace std;
const int N = 1e5 + 10;
const int R = 1e5;
int n, m;
int ccnt; // 动态开点计数器
int root[N * 80]; // 以 i 号节点为根的权值树的根节点编号
int deep[N], fa[N][20];
int ans[N];
vector<int> linker[N];
// 权值树节点结构
struct node {
int ls, rs; // 左右儿子
int sum, lei; // 最大值的大小和种类
} tree[N * 80]; // 权值树数组
void add(int u, int v) {
linker[u].push_back(v);
}
// LCA 预处理
void init(int now, int father) {
fa[now][0] = father;
deep[now] = deep[father] + 1;
for (int i = 1; i <= 18; i++)
fa[now][i] = fa[fa[now][i - 1]][i - 1];
for (int v : linker[now]) {
if (v == father) continue;
init(v, now);
}
return ;
}
int lca(int u, int v) {
if (deep[u] != deep[v]) {
if (deep[u] < deep[v]) swap(u, v);
for (int i = 18; i >= 0; i--)
if (deep[fa[u][i]] >= deep[v])
u = fa[u][i];
}
if (u == v) return u;
for (int i = 18; i >= 0; i--) {
if (fa[u][i] != fa[v][i]) {
u = fa[u][i];
v = fa[v][i];
}
}
return fa[u][0];
}
// 向上更新
void pushup(int id) {
if (lson == 0) {
tree[id].sum = tree[rson].sum;
tree[id].lei = tree[rson].lei;
return ;
}
if (rson == 0) {
tree[id].sum = tree[lson].sum;
tree[id].lei = tree[lson].lei;
return ;
}
// 如果相等，则选左儿子，因为左儿子的类型绝对小于右儿子
if (tree[lson].sum >= tree[rson].sum) {
tree[id].sum = tree[lson].sum;
tree[id].lei = tree[lson].lei;
} else {
tree[id].sum = tree[rson].sum;
tree[id].lei = tree[rson].lei;
}
}
// 单点更新：某个节点上增加一袋 v 类型的救济粮
void change(int &id, int l, int r, int v, int val) {
if (!id) id = ++ccnt;
if (l == r) {
tree[id].sum += val; // l == r 时，此区间只有一种救济粮，可以直接相加
tree[id].lei = v; // 类型变化
return ;
}
if (v <= mid) change(lson, l, mid, v, val);
else change(rson, mid + 1, r, v, val);
pushup(id);
}
// 合并两棵权值树：将 v 合并到 u 上
int merge(int u, int v, int l, int r) {
if (!u || !v) return u + v;
if (l == r) {
tree[u].sum += tree[v].sum; // 信息合并
tree[u].lei = l; // l == r时，此区间只有一种救济粮，可以直接相加
return u;
}
// 递归合并左右子树
tree[u].ls = merge(tree[u].ls, tree[v].ls, l, mid);
tree[u].rs = merge(tree[u].rs, tree[v].rs, mid + 1, r);
pushup(u);
return u;
}
// 统计答案：后序遍历合并子树的权值树
void cacl(int id, int fa) {
for (int v : linker[id]) {
if (v == fa) continue;
cacl(v, id);
root[id] = merge(root[id], root[v], 1, R);
}
// 处理当前节点的答案
if (tree[root[id]].sum == 0) ans[id] = 0;
else ans[id] = tree[root[id]].lei;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
// 建边
for (int i = 1, a, b; i < n; i++) {
cin >> a >> b;
add(a, b), add(b, a);
}
// LCA 预处理
init(1, 0);
// 处理修改操作（树上差分）
for (int i = 1, x, y, z; i <= m; i++) {
cin >> x >> y >> z;
change(root[x], 1, R, z, 1);
change(root[y], 1, R, z, 1);
change(root[lca(x, y)], 1, R, z, -1);
change(root[fa[lca(x, y)][0]], 1, R, z, -1);
}
// 统计答案
cacl(1, 0);
for (int i = 1; i <= n; i++)
cout << ans[i] << "\n";
return 0;
}
CF600E Lomsat gelral
题意：求以 \(1\) 为根时，每个子树中出现次数最多的颜色编号之和。
对于每个结点，存储 num 与 ans 两个值，分别表示出现次数最多的次数与出现次数最多的颜色编号之和。
合并的时候，对于点 \(u\) 左儿子 lc 与右儿子 rc，考虑三种情况：
lc.num > rc.num，那么将lc的信息放到 \(u\) 上lc.num < rc.num，那么将rc的信息放到 \(u\) 上lc.num = rc.num，那么 \(u\) 的num为lc.num或rc.num，ans就是lc.ans + rc.ans
注：本题可以使用树上启发式合并解决，空间消耗大幅度减少。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5 + 10;
int n, m, tot, cnt;
int c[N], rt[N];
ll ans[N];
vector<int> linker[N];
struct tree {
// lc 和 rc 分别表示左右儿子
// num 表示区间内颜色最多的节点个数
// ans 表示区间内的答案
int lc, rc, num;
ll ans;
} tree[N * 60];
void add(int x, int y) {
linker[x].push_back(y);
linker[y].push_back(x);
}
void pushup(int p) {
int ls = tree[p].lc, rs = tree[p].rc;
if (tree[ls].num > tree[rs].num) {
tree[p].num = tree[ls].num;
tree[p].ans = tree[ls].ans;
}
if (tree[ls].num < tree[rs].num) {
tree[p].num = tree[rs].num;
tree[p].ans = tree[rs].ans;
}
if (tree[ls].num == tree[rs].num) {
tree[p].num = tree[ls].num;
tree[p].ans = tree[ls].ans + tree[rs].ans;
}
return ;
}
int merge(int p, int q, int l, int r) {
if (!p || !q) return p + q;
if (l == r) {
tree[p].num += tree[q].num;
tree[p].ans = l;
return p;
}
int mid = (l + r) >> 1;
tree[p].lc = merge(tree[p].lc, tree[q].lc, l, mid);
tree[p].rc = merge(tree[p].rc, tree[q].rc, mid + 1, r);
pushup(p);
return p;
}
void update(int &p, int l, int r, int x) {
if (!p) p = ++cnt;
if (l == r) {
tree[p].num++;
tree[p].ans = l;
return ;
}
int mid = (l + r) >> 1;
if (x <= mid) update(tree[p].lc, l, mid, x);
else update(tree[p].rc, mid + 1, r, x);
pushup(p);
}
void dfs(int u, int fa) {
for (int v : linker[u]) {
if (v == fa) continue;
dfs(v, u);
rt[u] = merge(rt[u], rt[v], 1, N);
}
update(rt[u], 1, N, c[u]);
ans[rt[u]] = tree[rt[u]].ans;
}
int main() {
cin >> n, cnt = n;
for (int i = 1; i <= n; i++) {
cin >> c[i];
rt[i] = i;
}
for (int i = 1, x, y; i < n; i++) {
cin >> x >> y;
add(x, y);
}
dfs(1, 0);
for (int i = 1; i <= n; i++)
cout << ans[i] << " ";
return 0;
}
P3224 [HNOI2012] 永无乡
- 合并操作：使用并查集维护关系，然后使用
merge()进行根与根的合并 - 查询操作：记录区间内元素个数，然后针对
kth进行二分查找
#include <bits/stdc++.h>
#define ll long long
//#define lson tree[id].ls
//#define rson tree[id].rs
//#define mid ((l + r) / 2)
using namespace std;
const int N = 1e5 + 10;
const int R = 1e5;
int n, m, Q, ccnt;
int p[N], fa[N], ans[N];
int root[N * 80]; // 以 i 号节点为根的权值树的根节点编号
// 权值树节点结构
struct node {
int ls, rs; // 左右儿子
int sum; // 区间内元素的个数
} tree[N * 80];
int findroot(int x) {
if (fa[x] == x) return x;
else return fa[x] = findroot(fa[x]);
}
void pushup(int x) {
tree[x].sum = tree[tree[x].ls].sum + tree[tree[x].rs].sum;
}
int insert(int u, int l, int r) {
int rt = ++ccnt;
tree[rt].sum = 1;
if (l == r) return rt;
int mid = (l + r) >> 1;
if (u <= mid) tree[rt].ls = insert(u, l, mid);
else tree[rt].rs = insert(u, mid + 1, r);
return rt;
}
int merge(int u, int v, int l, int r) {
if (!u || !v) return u + v;
if (l == r) {
tree[u].sum += tree[v].sum;
return u;
}
int rt = ++ccnt, mid = (l + r) >> 1;
tree[rt].sum = tree[u].sum + tree[v].sum;
tree[rt].ls = merge(tree[u].ls, tree[v].ls, l, mid);
tree[rt].rs = merge(tree[u].rs, tree[v].rs, mid + 1, r);
return rt;
}
int query(int x, int k, int l, int r) {
if (tree[x].sum < k) return -1;
int mid = (l + r) / 2;
if (l == r) return ans[l];
if (tree[tree[x].ls].sum >= k) return query(tree[x].ls, k, l, mid);
else return query(tree[x].rs, k - tree[tree[x].ls].sum, mid + 1, r);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1, x; i <= n; i++) {
fa[i] = i, cin >> x;
root[i] = insert(x, 1, R);
ans[x] = i;
}
for (int i = 1, x, y; i <= m; i++) {
cin >> x >> y;
int p = findroot(x), q = findroot(y);
if (p != q) {
root[q] = merge(root[p], root[q], 1, R);
fa[p] = q;
}
}
char c;
int x, y;
cin >> Q;
while (Q--) {
cin >> c >> x >> y;
if (c == 'Q') cout << query(root[findroot(x)], y, 1, R) << "\n";
else {
int p = findroot(x), q = findroot(y);
if (p != q) fa[p] = q, root[q] = merge(root[p], root[q], 1, R);
}
}
return 0;
}
浙公网安备 33010602011771号