【学习笔记】李超线段树

前言

请问一下，\(\textup{Link-Cut Tree}\) 与李超树不是同一个东西吗？它们好像都是 \(\textup{LCT}\)，那应该没区别吧（迷雾）

当然今天讲的不是大名鼎鼎的 \(\textup{Link-Cut Tree}\)，不过名气与它也差不多。OK，废话不多说，开始进入我们的主题！

原理

李超线段树的定义：李超线段树是一种用于维护平面直角坐标系内线段关系的数据结构。

李超线段树的经典应用：给定一个平面直角坐标系，支持动态插入一条线段，对于每一个询问，给一条竖线，问这条竖线与所有线段的最高的交点（即 \(y\) 值最大），题目传送门。

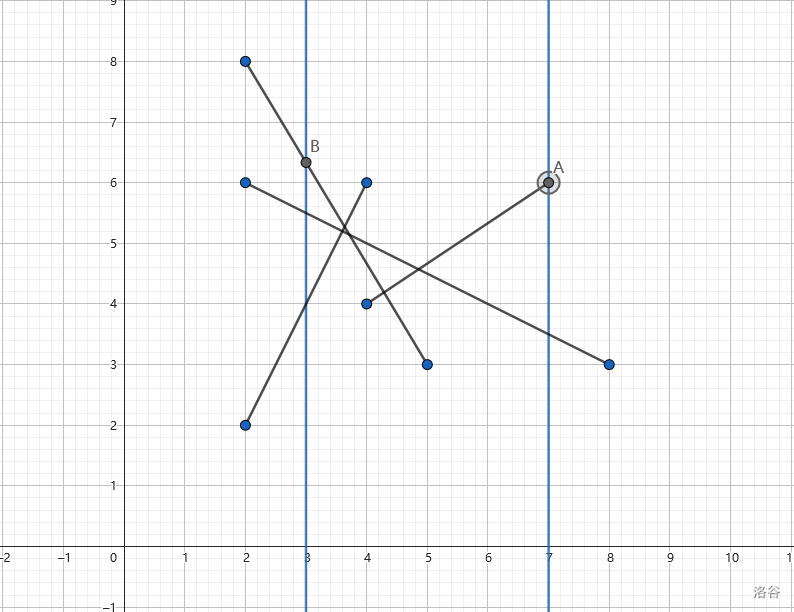
如上图，两条蓝色的直线就是两个询问，那么答案分别就是 \(A\) 点和 \(B\) 点。

这里我们要引入一个概念：最优势线段。最优势线段的定义：当前区间中点处最高的线段。

李超线段树维护的是有可能成为当前区间的最优势线段。某个节点的最优势线段在这个节点到根节点路径上所有最优势线段的之中。

为何要维护这个东西呢？因为如果你不维护它的话，那么你每加入一条线段就要把整个区间跑一遍，时间复杂度飞到 \(O(n^2)\)。

而如果像我们这样子维护的话，我们就不用每次加入线段都遍历整个区，而是可以在一个可以替换的区间停下。

---

OK，我们先看看如何插入线段。

我们可以找到以下几种情况：

• 该线段与当前线段树枚举到的区间不相交，此时直接返回即可。

• 该线段部分覆盖到了当前线段树枚举到的区间，递归到左右子区间继续处理，使得最后的线段能完全覆盖线段树上的区间。

• 该线段完全覆盖到了当前线段树枚举到的区间，则接着分讨：

  • 该线段在两个端点处值均比当前区间的最优势线段更大，则将当前区间的最优势线段设为该线段，然后返回（此时旧的最优势线段已经无用了）
  • 该线段在两个端点处的值均比当前区间的最优势线段更小，则返回（此时我们新加的线段也已经无用了）
  • 现在只剩下一个端点新加入的线段大，另一个端点区间的最优势线段大的情况，我们可以这样考虑。
    由于我们的线段树维护的是中点的最优势线段，所以我们需要判断一下新加入的线段和原先区间的最优势线段在中点位置的大小，并且更新改区间的最优势线段。
    因为这两个线段不能互相替代，所以我们并不能直接将一个线段舍弃，也就是说我们要将没被记录的线段往两边递归，以发挥它们的最大作用。但是由于在中点处未被记录的线段更小，所以在某一边该线段是完全小于被记录的线段的，所以不需要往该边递归，只需要往另一边递归即可。（被记录的线段指的是被存储到该区间的最优势线段，未被记录的线段指的是另一条线段）

这样子我们动态插入线段就搞定了，可以参照下面代码理解理解：

bool cmp(int i, int j, int x) {
    if (seg[i].k * x + seg[i].b - (seg[j].k * x + seg[j].b) > eps) return 1;
    if (seg[j].k * x + seg[j].b - (seg[i].k * x + seg[i].b) > eps) return 0;
    return i < j;
}

void change(int &x, int l, int r, int sl, int sr, int now) {
    if (r < sl || sr < l) return ; // 完全无连接
    if (!x) x = ++Tcnt; // 动态开点 
    if (sl <= l && r <= sr) { // 完全覆盖 
    	// 整个 [l, r] 都覆盖了 
        if (cmp(now, tree[x].id, l) && cmp(now, tree[x].id, r)) {
            tree[x].id = now; // 更新 
            return ;
        }
        
        // 什么用都没有，直接返回 
        if (cmp(tree[x].id, now, l) && cmp(tree[x].id, now, r))
            return ;
        
        int mid = (l + r) >> 1;
        
        // 这里原始最优势线段与新加入线段不能相互代替，因此要不断递归，发挥这两条线段的作用 
        if (cmp(now, tree[x].id, mid)) swap(now, tree[x].id); // 让中点较小的那个点作为 now，使接下来的更新更方便 
        if (cmp(now, tree[x].id, l)) change(tree[x].ls, l, mid, sl, sr, now); // 尽管中点更小，但是左端点更大。有用，因此递归 
        if (cmp(now, tree[x].id, r)) change(tree[x].rs, mid + 1, r, sl, sr, now); // 尽管中点更小，但是右端点更大。有用，因此递归 
    } else { // 部分覆盖（继续递归至完全覆盖） 
        int mid = (l + r) >> 1;
        change(tree[x].ls, l, mid, sl, sr, now), change(tree[x].rs, mid + 1, r, sl, sr, now);
    }
}

查询就更简单了，直接往下找到该区间，并且将路径上所有区间的最优势线段都拿出来比较一下，可以参照下面代码理解。

void solve(int x, int l, int r, int s) {
    if (!x || r < s || s < l) return ; // 遇到不合法的线段（即不包含 s 的线段）要返回 
    if (cmp(tree[x].id, ansid, s)) ansid = tree[x].id; // 往这一条路上一直找答案 
    if (l == r) return ;
    
    int mid = (l + r) >> 1;
    solve(tree[x].ls, l, mid, s), solve(tree[x].rs, mid + 1, r, s);
}

到这里，李超线段树就完成了！！！

考虑一下时间复杂度，我们知道线段会在线段树上分成 \(\log_2 n\) 个区间，而看到我们插入操作，分成的每个区间不会再分裂，而只会往一边更新，最多更新 \(\log_2 n\) 层，所以时间复杂度是 \(O({\log^2}_n)\)。

然后我们就可以来看这道板题，没什么好说的，直接上代码。

唯一的坑点就是精度问题。

#include <bits/stdc++.h>
using namespace std;

const double eps = 1e-8;
const int N = 1e5 + 10;

const int mod1 = 39989;
const int mod2 = 1e9;

int T, Lastans, n = 39989, m, Tcnt, Rt, ansid;
struct Line { double k, b; } seg[N * 4];
struct Tree { int ls, rs, id; } tree[N * 4];

bool cmp(int i, int j, int x) {
    if (seg[i].k * x + seg[i].b - (seg[j].k * x + seg[j].b) > eps) return 1;
    if (seg[j].k * x + seg[j].b - (seg[i].k * x + seg[i].b) > eps) return 0;
    return i < j;
}

void change(int &x, int l, int r, int sl, int sr, int now) {
    if (r < sl || sr < l) return ; // 完全无连接 
    if (!x) x = ++Tcnt; // 动态开点 
    if (sl <= l && r <= sr) { // 完全覆盖 
    	// 整个 [l, r] 都覆盖了 
        if (cmp(now, tree[x].id, l) && cmp(now, tree[x].id, r)) {
            tree[x].id = now; // 更新 
            return ;
        }
        
        // 什么用都没有，直接返回 
        if (cmp(tree[x].id, now, l) && cmp(tree[x].id, now, r))
            return ;
        
        int mid = (l + r) >> 1;
        
        // 这里原始最优势线段与新加入线段不能相互代替，因此要不断递归，发挥这两条线段的作用 
        if (cmp(now, tree[x].id, mid)) swap(now, tree[x].id); // 让中点较小的那个点作为 now，使接下来的更新更方便 
        if (cmp(now, tree[x].id, l)) change(tree[x].ls, l, mid, sl, sr, now); // 尽管中点更小，但是左端点更大。有用，因此递归 
        if (cmp(now, tree[x].id, r)) change(tree[x].rs, mid + 1, r, sl, sr, now); // 尽管中点更小，但是右端点更大。有用，因此递归 
    } else { // 部分覆盖（继续递归至完全覆盖） 
        int mid = (l + r) >> 1;
        change(tree[x].ls, l, mid, sl, sr, now), change(tree[x].rs, mid + 1, r, sl, sr, now);
    }
}

void solve(int x, int l, int r, int s) {
    if (!x || r < s || s < l) return ; // 遇到不合法的线段（即不包含 s 的线段）要返回 
    if (cmp(tree[x].id, ansid, s)) ansid = tree[x].id; // 往这一条路上一直找答案 
    if (l == r) return ;
    
    int mid = (l + r) >> 1;
    solve(tree[x].ls, l, mid, s), solve(tree[x].rs, mid + 1, r, s);
}

int main() {
    cin >> T;
    while (T--) {
        int id, x, sx, sy, ex, ey;
        cin >> id;
        if (id == 0) {
            ansid = 0;
            cin >> x, x = (x + Lastans - 1) % n + 1;
            solve(1, 1, n, x), Lastans = ansid;
            cout << ansid << endl;
        } else {
            cin >> sx >> sy >> ex >> ey;
            
            sx = (sx + Lastans - 1) % mod1 + 1, sy = (sy + Lastans - 1) % mod2 + 1;
			ex = (ex + Lastans - 1) % mod1 + 1, ey = (ey + Lastans - 1) % mod2 + 1;
            
			if (ex < sx) swap(sx, ex), swap(sy, ey); // 不写这个的就是 bangbangt 
            if (ex != sx) m++, seg[m].k = 1.0 * (ey - sy) / (ex - sx), seg[m].b = 1.0 * sy - seg[m].k * sx;
            else m++, seg[m].k = 0, seg[m].b = max(sy, ey);

            change(Rt, 1, n, sx, ex, m);
        }
    }
    return 0;
}