BUAA_OO_2021_第一单元总结博客
第一单元总结博客
一.历次作业分析
-
第一次作业
(1)程序结构分析
第一次作业可谓是让人头大,第一次接触面向对象的题目非常不适应,所以我的第一次作业完全是以面向过程的思想来完成的。在这里提个醒,我由于脑子不太清晰,截止前十五分钟内交了一版没有通过中测的代码(原来的版本已经通过了中测),导致第一次直接与互测说拜拜,所以这里提醒各位不要犯一些这样的低级错误。
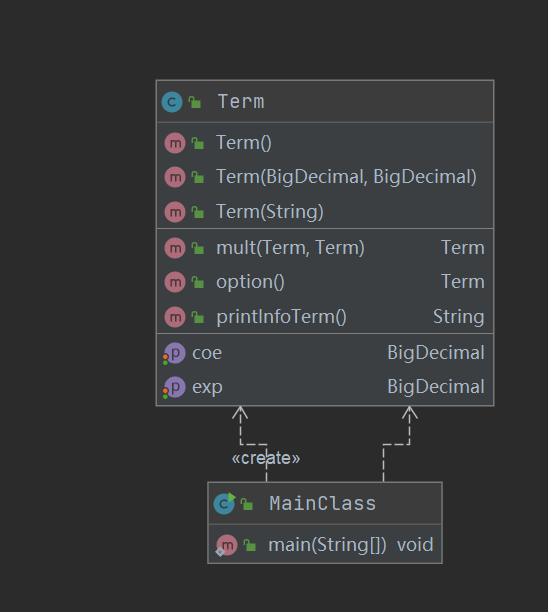
对于第一次作业,我直接采用了化整为零的想法,先将由加减号连接的每一项分开,再将由乘号相连的每一个因子(第一次作业里面只有常数和x的幂次方),将每一项进行合并,得到一个带有系数的“类幂次数”,然后直接通过加法法则得到导函数。由于思路简陋,所以只用到了两个类,极其丑陋。在数据存储方面,我使用了Arraylist进行存储,遍历和添加起来还是比较方便的。
![image]()
在这里我只设计了一个Term类,有系数和指数,所以我在处理输入串的时候,其实是把每一项都合并到一个Term的对象中,这样做非常不可取,因为强行将两个属性不一样的类扯成一个类,在设计上是不明智的,所以在第二次作业中,我就改掉了这个设计。
(2)bug分析
由于我的第一次作业全程面向过程,所以也有一些难以避免的错误。最严重的就是一个数组越界的错误。这主要是因为我在对每一项求导的时候,由于每一项前面有一个符号,而我在存储这个符号的时候,使用了char[],进行初始化以后,这个东西的大小就固定了,而由于存在表达式中的第一项前面没有符号的情况,所以在我的程序中可能存在对这个字符数组的最前面进行添加的操作,在这个时候,显而易见的就是字符数组由于我的这个操作会越界。
其次,由于第一次作业没有检查格式的要求,所以我实际上把所有的空格,tab以及连续的正负号和指数符号**都进行了处理,这样对后面是非常不利的,所以我充分建议各位对于输入串不要进行处理,而采用我后文提到的递归下降的思路。
(3)复杂度分析
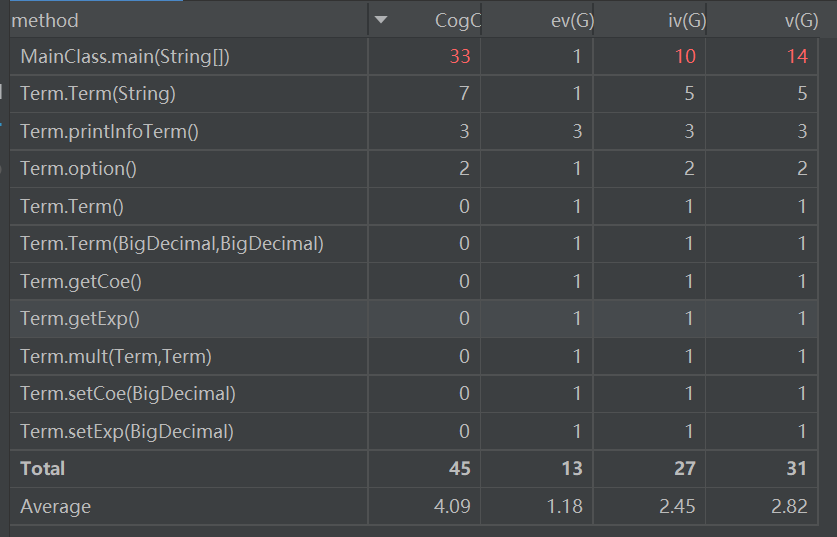
可见,由于第一次作业完全面向过程,方法的复杂度由于总共才两个类,看上去貌似还行?当然不可避免的就是main()的极多调用了。
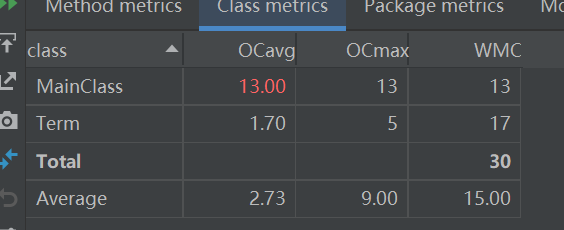
主类的复杂度不可避免的爆表了,全是面向过程的锅啊……全部以面向过程的思想来解析输入的字符串会使主类疯狂调用(也和我只设计了一个Term类有关),所以总结来说,应该更加明确“对象”到底是什么,不能模糊地就把常数和x的幂次就混到一起。
-
第二次作业
(1)程序结构分析
第二次作业相比于第一次作业只能说是难度上的爆炸。不仅添加了sin和cos(里面的因子只能是x,这里还比较良心),还添加了表达式的嵌套规则,这一下子就使得我们的表达式的类型变得非常丰富,理论上括号可以达到无数层(当然在我们的题目中是限制了输入串的长度的)。我最开始没有任何思路,后来根据指导书的“化整为零”的思想,准备采取这样的思路:先将每一个项根据每一个不在括号内的加减号分开,然后将每一个项中的每一个因子(包括表达式因子)通过每一个不在括号内的乘号分开,然后利用双重for循环,通过乘法法则和加法法则,得到导函数。但是我们在这里需要考虑一个非常严重的问题,就是当我们在这里其实是把表达式因子看成与sin,cos和常数以及x的幂次相同地位的“因子”,那我们在项这个类中存储因子的时候使用了一个因子的容器,然后,由于表达式又是由每一个项组成,所以我们需要另一个容器来存储每一项,这时候细想就会发现一个非常严重的问题:ExprTerm和NormalTerm发生了循环嵌套。我最开始觉得这里是一个死胡同,但经过分析发现,尽管这里有着逻辑上的错误,但是,我们的目的是通过递归得到一个导函数(其本质上就是一个字符串),而且由于第二次作业也不需要格式检查,所以这里我们的输入一定有对应的输出,所以只要这个输入得表达式是正确的,无论递归多少次,总会返回一个字符串,因为即使是有嵌套的表达式类,递归的重点就是这些最基本的类;想到这里我豁然开朗,就开始了这种递归的思路,最后也成功通过了中测。在这一次作业中我使用的类的数量就非常多了,整体程序也有了面向对象的思想。
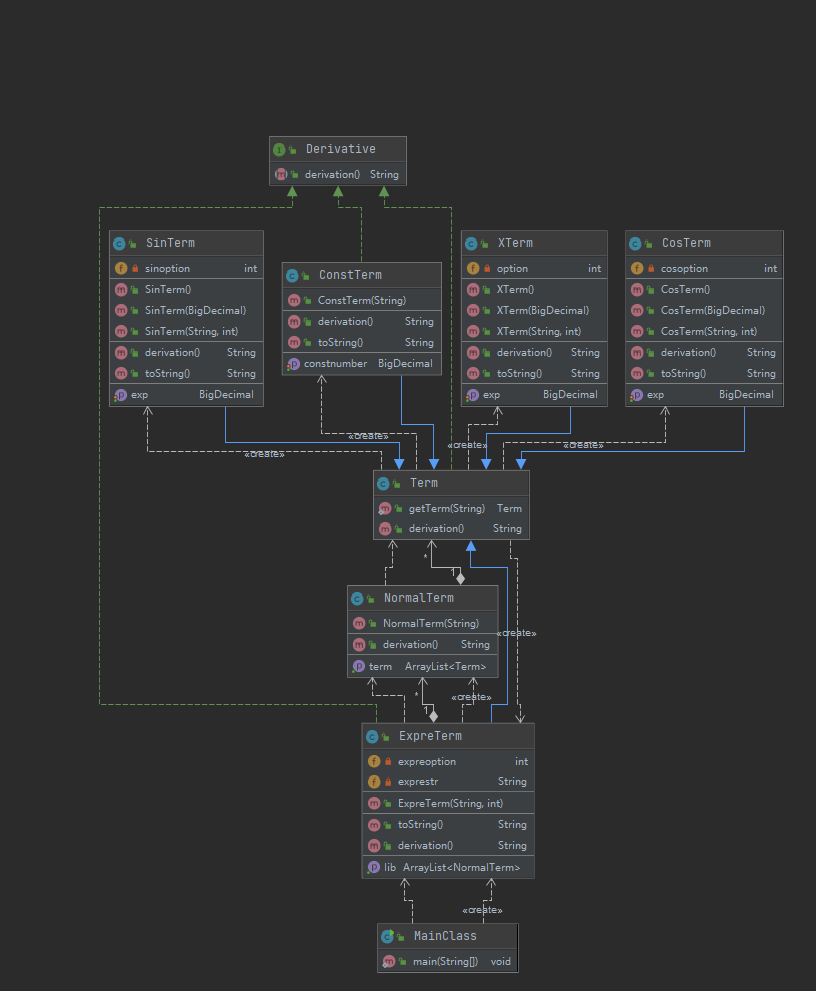
![image]()
类图上还是比较清晰的,但是项这个类和因子类的关联似乎不是很大。我设置了一个公共父类,最开始的想法只是想单纯给所有的子类继承一个求导方法,甚至没有把表达式因子从Term中继承。但是写到一半我发现,一旦我把表达式因子也归到Term的子类中,我不就可以实现我的递归的思路了吗?比如,我在对每个因子求导的时候需要调用每一个因子自己的求导方法,那当我对一个表达式因子求导的时候,不久正好可以又像上文所说的那样从项开始,接着到因子层面,递归到最后返回一个字符串,也就完美解决了嵌套求导这个问题。写到后来我发现,其实Term的意义绝不仅仅是一个给其他银子类继承一个方法这么简单,实际上是,这个Term,充当了一个抽象父类的作用,所以我在NormalTerm(项)这个类中声明容器的时候,就可以直接生命Arraylist
,这样实际上我可以把所有Term的子类都存到这个容器里面;写到这,我才真正意识到Term这个父类的真正作用,统一管理所有因子类并且为子类提供求导方法(不过我在这里还是用求导接口实现了……手动捂脸hhhhh)。在这里我可以对比一下我这种递归思路和递归下降思路,递归下降是一种非常自然的思想,不需要对输入做任何处理,直接递归调用每一层的parse函数,但我的这种递归方法,实际上是对输入进行一定处理以后,从类的结构组成上进行递归,所以我的这种递归的前提必须是输入串要是合法的。很明显,递归下降如果parse函数没有写错,基本不会有出错的可能,但由于我对输入串进行过处理,在这些处理中有非常多的情况需要考虑,一旦考虑不周(比如忽略tab只考虑空格,或者只考虑两个符号相连忽略三个符号相连)就会出错,所以第三次作业我就直接采取了递归下降的做法。 (2)bug分析
说到这个bug分析,只能说,由于我完成的太快,有点飘,根本没有做认真的测试,最后直接没通过强测,没错,第二周我还是没有见到互测的界面(手动捂脸)。主要的问题在于我在处理表达式因子的时候,在“去除其可能存在在的括号”的时候,我是直接判断这个表达式的第一个和最后一个是不是分别为“(”和“)”,这样就有可能直接将“(1+x)*(2+x)”这种数据变成了不合法的,报错RE也就不奇怪了;除了这个大bug以外,还有就是我对于每一项前面的符号的处理,由于一个下标的失误,所以负号我都没有考虑,直接导致大部分数据点都是WA;这两个看似低级的错误实际上体现了我思路的局限性,后来我直接先对每个表达式先加一层括号,解决了这个问题。
(3)复杂度分析
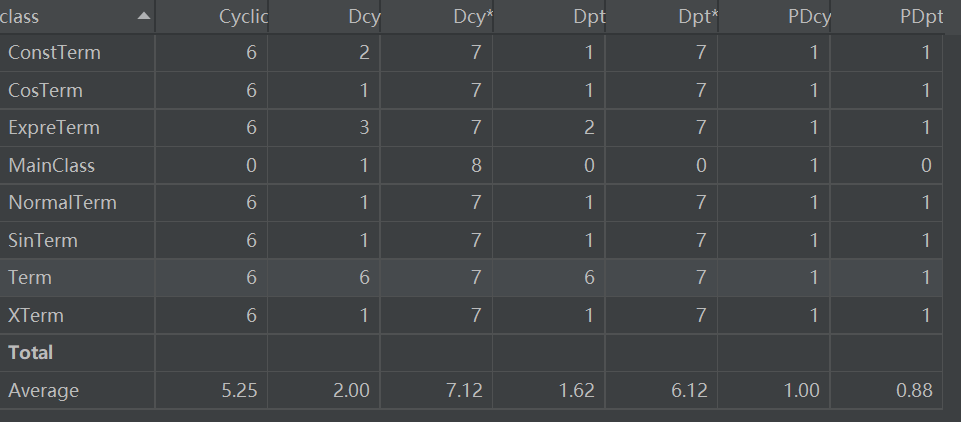
相关性还是挺高的;
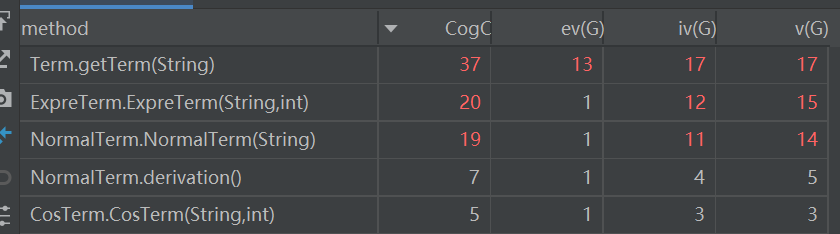
可见,这次作业的构造方法是一个大问题,还是比较复杂的,主要是因为我前面提到的循环嵌套的问题,导致了非常多的递归构造。表达式中嵌套表达式,内层的表达式又会嵌套表达式,这样一直调用,最后导致复杂度上升非常快。
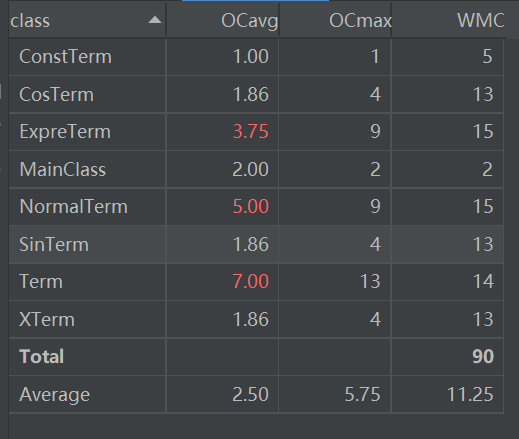
在类度量图中可以发现,ExpreTerm和NolmalTerm以及Term的圈复杂度还是比较高的,主要原因是前面所讲到的“循环嵌套”的问题导致递归层数过多导致的。
-
第三次作业
(1)程序结构分析
第三次作业,好家伙,又是一波重构。这次增加我认为最阴间的要求,格式检查,因为我前面两次作业全都对输入的字符串进行了处理,这样在需要格式检查的时候直接凉凉了。解决这个问题最好的办法就是递归下降。对于我这种普通学生,初次听到递归下降的时候完全没有头绪,后来还是通过研讨课的大佬的ppt才完整地了解了这个思路。这个思路其实就是,对于每一个语法结构,分析其终止符,比如对于表达式中的每一项,终止符就是“+”和“-”,然后利用while语句,对输入字符串进行递归的解析,也就是说,对于每一个语法成分,我们都需要写一个parse函数,比如对于表达式类ExprTerm,我们需要parseExpr,对于项这个类我们需要parseTerm,对于因子我们需要parseFactor,类似的,对于sin,cos等我们也需要相应的parse函数,那么递归下降最核心的思想是什么呢?我通过这一小段代码的实例来解释这个问题:
int parseTerm(){ int ans = parseTerm(); while(str[sign]=='+'||str[sign]=='-'){ if (str[sign]=='+'){ ans += parseTerm; sign++; } else{ ans -= parseTerm; sign++; } } return ans; }我们可以发现,按照Expr->Term->Factor->x,const,sin,cos,Expr这个层次把所以的parse函数像我上面这段代码一样写完以后就形成了一个绝妙的结构,那就是,顶层的parse函数递归调用底层的parse函数,每一层根据while循环(这里是一个比较重要的东西,叫做“左递归”的问题,后文会继续分析)继续往下解析调用下一层的parse函数,最后完成整个输入串的解析。如果对于上文的所有思想已经了解透彻的话,可以非常敏锐地发现,如果在这个过程中,某一个成分遇到了不符合题目要求的字符,我们就可以直接判断“WRONG FORMAT!”了,而这也就是递归下降的最大好处,它是一个非常自然的解析过程,先默认输入串合法,进行递归地解析,然后对于每一层,如果出现了不合法的内容,直接抛出异常,完美解决了我们的作业要求。
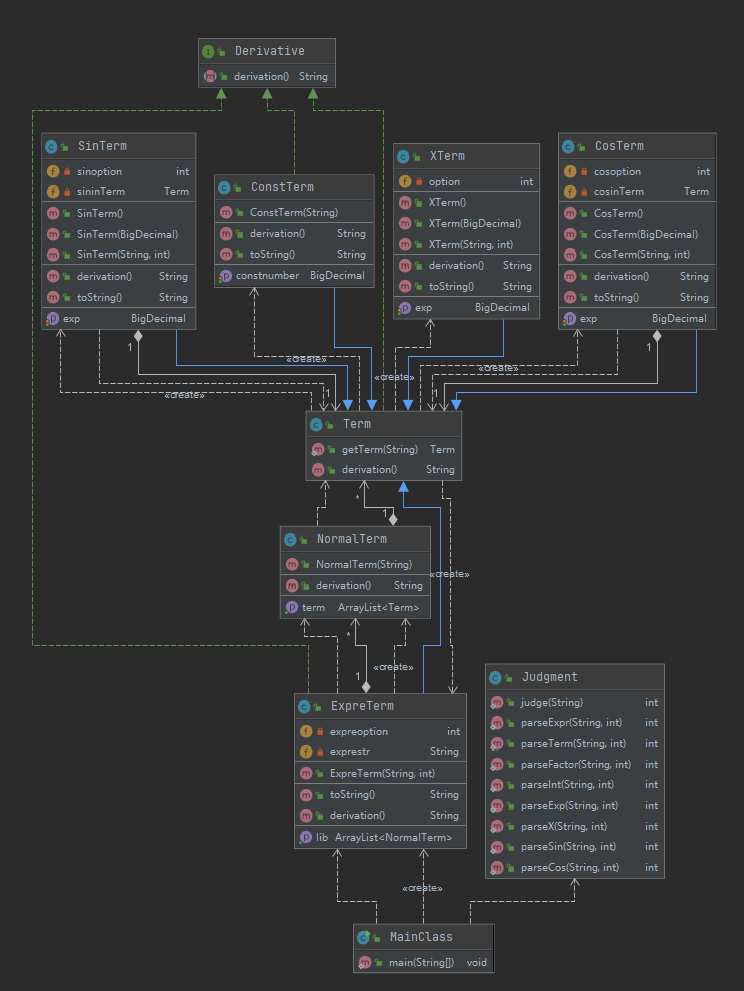
从类图中我们可以看到,结构还是比较清晰的,所有基本的因子类都是继承自一个公共的父类,这与第二次作业的类的设计基本是一致的,除此之外,由于我第三次作业有点偷懒,所以就直接加了一个判断模块,所以Judement和几个主要的类也没有关联。大体思路是,利用递归下降对输入串进行解析,如果合法,就传给我在第二次作业中的递归求导,如果不合法,直接就判断WF了。
(2)bug分析
这里仅存的一个bug就是我没有考虑指数可能存在超过int范围的情况,主要也是由于整个工程太大,根本没有考虑这些细节,在以后的作业中要努力改正这个缺点。除此之外,由于递归下降的思路完美适应了我们的作业要求,所以只要parse函数没有写错,判断格式和求导不会有什么大问题(在这里我偷懒,直接加了一个判断模块,如果合法的话,就跟第二次作业一样的处理,只不过改了一下sin和cos的嵌套求导问题)。
(3)复杂度分析
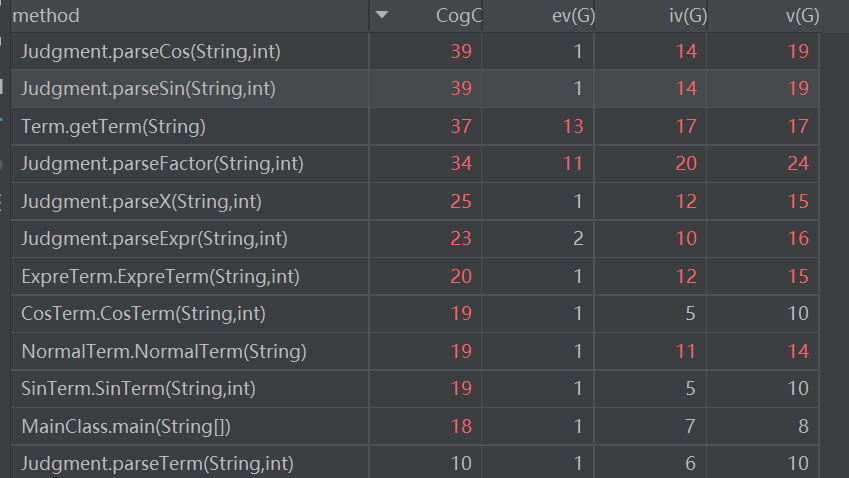
显而易见的就是我的每一个类的构造方法都非常复杂,而且递归下降的parse方法也比较复杂,分析认为还是因为在构造的时候也是一个递归的过程,而没有采用在递归下降的过程中一起实现构造的原因。
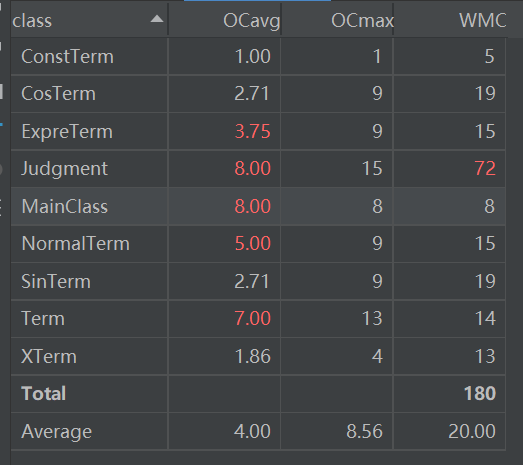
由于第三次作业的求部分实际上与第二次作业没有什么不同,所以ExpreTerm和NolmalTerm以及Term的圈复杂度还是比较高(主要也是因为求导部分没有进行重构导致),同时Judgment由于采用递归下降的思想,递归层数也比较多,导致其圈复杂度也比较高。
(4)发现别人程序bug策略
第三次作业我终于见到了互测的界面(……估计也没谁了),但是非常有意思的是,好像第三周大家找bug的兴趣都不是很高,全程就只有一位同学交了一份数据,我也没被hack到。我读了几位同学的代码,有的同学其实不适用递归下降写的判断,而是用一种类似穷举的方法,这就很好找出毛病了,只要把已知的存在的样例拿去hack就行,但这次我用评测机跑了几位同学的代码都没有什么太大的问题,所以也没有成功hack到别人。
二.重构经历总结
我的每一次作业都没有重构,但是在作业之间还是有一些比较大的调整的,我也把这些调整归为“重构”,在这一节进行分析。主要的调整就是在第一次作业和第二次作业之间的大调整。第一次作业在前面的分析中已经可以看到,完全面向过程,导致main()方法调用过多;所以我在第二次作业的时候,调整了类的数量(当然这也跟三角函数的加入有关),对每一个不同的类真正实现了继承的关系,除此之外,还调整了求导的算法,从强行把一个项变成一个一个因子,变成用容器来装同一个项里面的每一个因子对象,然后用两重for循环解决求导的问题,很明显的是,在第二次作业的复杂度中,main()方法的调用没有第一次作业中那么离谱,但是由于还是没有采用完全的递归下降的解析方法,所以表达式类的构造方法的复杂度还是比较高,但这是由于递归调用过多导致的问题,这也是在我的预期之内的。总体来说,整个调整过程还是很自然的,适应了题目变化,但还是没有综合考虑的思想,导致到了第三次作业的时候就只能直接加一个新的模块单独判断合法性,这样整体上来看这个判断模块就显得有点格格不入。整体考虑的思想还要在以后的单元作业中更加贯彻。
三.心得体会
- 个人体会最大的一点就是:面向对象的思想在我的编程习惯中,从几乎没有到有了很大体现。从接触编程开始我所有的思维方式都是面向过程,把重点放在每一个函数的实现上,但学习了第一单元OO以后,我对每个类具体的方法倒不是那么关心,反而会去操心各个类之间的关联,以及怎么设计父类和继承关系或者接口。完成第三次作业以后,对比自己的第一次的类图,只能说第一次的自己是一个OO上的婴儿,现在至少已经在蹒跚学步了,第二单元多线程电梯作业拿上就要开始了,希望我们能在这个接下来的单元的学习中更加深化自己面向对象的思想,并将OO的思想带到以后的学习工作中,高效地解决问题。
- 除此之外,还提前学习了一些大三编译中的递归下降的语法分析的方法。在这里也非常感谢几位研讨课上积极分享的同学,如果没有这几位热心的同学,我是不可能在这么短的时间内把递归下降算法搞明白的。同时,我也希望助教可以再花一些时间给我们讲授一些作业需要用到的相关背景和知识,或者提供一些博客资料给我们,个人觉得助教在我们写作业的过程中的作用不是特别大。
- 总体来说,第一单元的OO学习确实给了自己比较大的提升,面向对象的思想也在代码中慢慢地培养,希望我们都能在接下来的单元学习中继续探索面向对象思想的更深层次的奥义,各位同学共勉!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号