回溯 rating 1900~2200
P1
给定一个非负整数数组 A,如果该数组每对相邻元素之和是一个完全平方数,则称这一数组为正方形数组。
返回 A 的正方形排列的数目。两个排列 A1 和 A2 不同的充要条件是存在某个索引 i,使得 A1[i] != A2[i]。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/number-of-squareful-arrays
- 剪枝要尽可能提前
- 注意计算结果是否超过类型范围
示例 1:
输入:[1,17,8]
输出:2
解释:
[1,8,17] 和 [17,8,1] 都是有效的排列。
提示:
1 <= A.length <= 12
0 <= A[i] <= 1e9
class Solution {
bool isSqure(int val) {
int left = 0;
int right = val;
while (left < right) {
int mid = left + (right - left + 1) / 2;
if ((long)mid * mid <= val) {
left = mid;
} else {
right = mid - 1;
}
}
return (long)left * left == val;
}
void dfs(vector<int>& nums, int idx, vector<int>& buf, vector<int>& visit, int& res) {
if (idx == nums.size()) {
res += 1;
return;
}
for (int i = 0; i < nums.size(); ++i) {
if (visit[i]) {
continue;
}
if (i > 0 && nums[i] == nums[i - 1] && !visit[i - 1]) {
continue;
}
if (idx > 0 && !isSqure(nums[i] + buf.back())) {
continue;
}
buf.emplace_back(nums[i]);
visit[i] = 1;
dfs(nums, idx + 1, buf, visit, res);
visit[i] = 0;
buf.pop_back();
}
}
public:
int numSquarefulPerms(vector<int>& nums) {
int n = nums.size();
int res = 0;
vector<int> buf;
vector<int> visit(n);
sort(nums.begin(), nums.end());
dfs(nums, 0, buf, visit, res);
return res;
}
};
P2
游戏中存在两种角色:
好人:该角色只说真话。
坏人:该角色可能说真话,也可能说假话。
给你一个下标从 0 开始的二维整数数组 statements ,大小为 n x n ,表示 n 个玩家对彼此角色的陈述。具体来说,statements[i][j] 可以是下述值之一:
0 表示 i 的陈述认为 j 是 坏人 。
1 表示 i 的陈述认为 j 是 好人 。
2 表示 i 没有对 j 作出陈述。
另外,玩家不会对自己进行陈述。形式上,对所有 0 <= i < n ,都有 statements[i][i] = 2 。
根据这 n 个玩家的陈述,返回可以认为是 好人 的 最大 数目。
输入:statements = [[2,1,2],[1,2,2],[2,0,2]]
输出:2
解释:每个人都做一条陈述。
- 0 认为 1 是好人。
- 1 认为 0 是好人。
- 2 认为 1 是坏人。
以 2 为突破点。 - 假设 2 是一个好人:
- 基于 2 的陈述,1 是坏人。
- 那么可以确认 1 是坏人,2 是好人。
- 基于 1 的陈述,由于 1 是坏人,那么他在陈述时可能:
- 说真话。在这种情况下会出现矛盾,所以假设无效。
- 说假话。在这种情况下,0 也是坏人并且在陈述时说假话。
- 在认为 2 是好人的情况下,这组玩家中只有一个好人。
- 假设 2 是一个坏人:
- 基于 2 的陈述,由于 2 是坏人,那么他在陈述时可能:
- 说真话。在这种情况下,0 和 1 都是坏人。
- 在认为 2 是坏人但说真话的情况下,这组玩家中没有一个好人。
- 说假话。在这种情况下,1 是好人。
- 由于 1 是好人,0 也是好人。
- 在认为 2 是坏人且说假话的情况下,这组玩家中有两个好人。
在最佳情况下,至多有两个好人,所以返回 2 。
注意,能得到此结论的方法不止一种。
- 说真话。在这种情况下,0 和 1 都是坏人。
- 基于 2 的陈述,由于 2 是坏人,那么他在陈述时可能:
n == statements.length == statements[i].length
2 <= n <= 15
statements[i][j] 的值为 0、1 或 2
statements[i][i] == 2
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/maximum-good-people-based-on-statements
class Solution {
int cal(int n, vector<int>& buf, vector<vector<int>>& statements) {
for (int i = 0; i < n; ++i) {
if (buf[i] != 1) {
continue;
}
for (int j = 0; j < n; ++j) {
if ((statements[i][j] == 0 && buf[j] == 1) || (statements[i][j] == 1 && buf[j] == 0)) {
return 0;
}
}
}
return accumulate(buf.begin(), buf.end(), 0);
}
void backtrack(vector<vector<int>>& statements, int idx, int n, vector<int>& buf, int& res) {
if (idx == n) {
res = max(res, cal(n, buf, statements));
return;
}
buf.emplace_back(0);
backtrack(statements, idx + 1, n, buf, res);
buf.pop_back();
buf.emplace_back(1);
backtrack(statements, idx + 1, n, buf, res);
buf.pop_back();
}
public:
int maximumGood(vector<vector<int>>& statements) {
int res = 0;
int n = statements.size();
vector<int> buf;
backtrack(statements, 0, n, buf, res);
return res;
}
};
P3
你被安排了 n 个任务。任务需要花费的时间用长度为 n 的整数数组 tasks 表示,第 i 个任务需要花费 tasks[i] 小时完成。一个 工作时间段 中,你可以 至多 连续工作 sessionTime 个小时,然后休息一会儿。
你需要按照如下条件完成给定任务:
如果你在某一个时间段开始一个任务,你需要在 同一个 时间段完成它。
完成一个任务后,你可以 立马 开始一个新的任务。
你可以按 任意顺序 完成任务。
给你 tasks 和 sessionTime ,请你按照上述要求,返回完成所有任务所需要的 最少 数目的 工作时间段 。
测试数据保证 sessionTime 大于等于 tasks[i] 中的 最大值 。
https://leetcode.cn/problems/minimum-number-of-work-sessions-to-finish-the-tasks/description/
输入:tasks = [3,1,3,1,1], sessionTime = 8
输出:2
解释:你可以在两个工作时间段内完成所有任务。
- 第一个工作时间段:完成除了最后一个任务以外的所有任务,花费 3 + 1 + 3 + 1 = 8 小时。
- 第二个工作时间段,完成最后一个任务,花费 1 小时。
n == tasks.length
1 <= n <= 14
1 <= tasks[i] <= 10
max(tasks[i]) <= sessionTime <= 15
class Solution {
int recursive(int need, vector<int>& tasks, int sessionTime) {
int res = INT_MAX;
if (need == 0) {
return 0;
}
if (cache[need]) {
return cache[need];
}
if (times[need] <= sessionTime) {
return 1;
}
for (int sub = (need - 1 ) & need; sub; sub = (sub - 1) & need) {
int rest = need ^ sub;
cache[sub] = recursive(sub, tasks, sessionTime);
cache[rest] = recursive(rest, tasks, sessionTime);
res = min(cache[sub] + cache[rest], res);
}
return cache[need] = res;
}
public:
int minSessions(vector<int>& tasks, int sessionTime) {
int n = tasks.size();
int need = 1 << n;
memset(cache, 0, sizeof(cache));
for (int i = 0; i < need; ++i) {
int sum = 0;
for (int j = 0; j < n; ++j) {
if ((1 << j) & i) {
sum += tasks[j];
}
}
times[i] = sum;
}
return recursive(need - 1, tasks, sessionTime);
}
private:
int cache[32000];
int times[32000];
};
P4
给你一个由正整数组成的数组 nums 和一个 正 整数 k 。
如果 nums 的子集中,任意两个整数的绝对差均不等于 k ,则认为该子数组是一个 美丽 子集。
返回数组 nums 中 非空 且 美丽 的子集数目。
nums 的子集定义为:可以经由 nums 删除某些元素(也可能不删除)得到的一个数组。只有在删除元素时选择的索引不同的情况下,两个子集才会被视作是不同的子集。
https://leetcode.cn/problems/the-number-of-beautiful-subsets/
输入:nums = [2,4,6], k = 2
输出:4
解释:数组 nums 中的美丽子集有:[2], [4], [6], [2, 6] 。
可以证明数组 [2,4,6] 中只存在 4 个美丽子集。
1 <= nums.length <= 20
1 <= nums[i], k <= 1000
class Solution {
void backtrack(int idx, vector<int>& nums, int k, int cnt, int& res) {
if (idx == nums.size()) {
res += static_cast<int>(cnt != 0);
return;
}
backtrack(idx + 1, nums, k, cnt, res);
int num = nums[idx];
if (buf[num + k] || (num - k >= 0 && buf[num - k])) {
return;
}
++buf[num];
backtrack(idx + 1, nums, k, cnt + 1, res);
--buf[num];
}
public:
int beautifulSubsets(vector<int>& nums, int k) {
int res = 0;
int cnt = 0;
memset(buf, 0, sizeof(buf));
backtrack(0, nums, k, 0, res);
return res;
}
private:
int buf[3000];
};
P5
给你 nums ,它是一个大小为 2 * n 的正整数数组。你必须对这个数组执行 n 次操作。
在第 i 次操作时(操作编号从 1 开始),你需要:
选择两个元素 x 和 y 。
获得分数 i * gcd(x, y) 。
将 x 和 y 从 nums 中删除。
请你返回 n 次操作后你能获得的分数和最大为多少。
函数 gcd(x, y) 是 x 和 y 的最大公约数。
https://leetcode.cn/problems/maximize-score-after-n-operations/description/
输入:nums = [3,4,6,8]
输出:11
解释:最优操作是:
(1 * gcd(3, 6)) + (2 * gcd(4, 8)) = 3 + 8 = 11
提示:
1 <= n <= 7
nums.length == 2 * n
1 <= nums[i] <= 106
class Solution {
int gcd(int a, int b) {
if (a < b) {
return gcd(b, a);
}
return a % b == 0 ? b : gcd(b, a % b);
}
int dfs(int mask, int i, unordered_map<int,int>& buf) {
int res = 0;
if (mask == 0) {
return 0;
}
if (cache[mask][i] != 0) {
return cache[mask][i];
}
for (auto&& [key, value] : buf) {
if ((mask & key) == key) {
res = max(res, value * i + dfs(mask ^ key, i + 1, buf));
}
}
return cache[mask][i] = res;
}
public:
int maxScore(vector<int>& nums) {
int n = nums.size();
int limit = 1 << n;
vector<int> temp;
unordered_map<int,int> buf;
memset(cache, 0, sizeof(cache));
for (int i = 0; i < limit; ++i) {
if (__builtin_popcount(i) == 2) {
temp.clear();
for(int j = 0; j < n; ++j) {
if ((1 << j) & i) {
temp.emplace_back(nums[j]);
}
}
buf[i] = gcd(temp[0], temp[1]);
}
}
return dfs((1 << n) - 1, 1, buf);
}
private:
int cache[16385][8];
};
P6
给你一个整数 n ,请你找到满足下面条件的一个序列:
整数 1 在序列中只出现一次。
2 到 n 之间每个整数都恰好出现两次。
对于每个 2 到 n 之间的整数 i ,两个 i 之间出现的距离恰好为 i 。
序列里面两个数 a[i] 和 a[j] 之间的 距离 ,我们定义为它们下标绝对值之差 |j - i| 。
请你返回满足上述条件中 字典序最大 的序列。题目保证在给定限制条件下,一定存在解。
一个序列 a 被认为比序列 b (两者长度相同)字典序更大的条件是: a 和 b 中第一个不一样的数字处,a 序列的数字比 b 序列的数字大。比方说,[0,1,9,0] 比 [0,1,5,6] 字典序更大,因为第一个不同的位置是第三个数字,且 9 比 5 大。
链接:https://leetcode.cn/problems/construct-the-lexicographically-largest-valid-sequence
示例 1:
输入:n = 3
输出:[3,1,2,3,2]
解释:[2,3,2,1,3] 也是一个可行的序列,但是 [3,1,2,3,2] 是字典序最大的序列。
提示:
1 <= n <= 20
class Solution {
void backtrack(int n, int idx, vector<int>& buf, vector<int>& used, vector<int>& res) {
if (idx == 2 * n - 1) {
res = buf;
return;
}
if (buf[idx] != 0) {
if (!res.empty() && res[idx] > buf[idx]) {
return;
}
backtrack(n, idx + 1, buf, used, res);
return;
}
for (int i = n; i >= 1; --i) {
if (used[i] || (i != 1 && idx + i >= (2 * n - 1)) || (i != 1 && buf[idx + i] != 0) || (!res.empty() && res[idx] > i)) {
continue;
}
buf[idx] = i;
if (i != 1) {
buf[idx + i] = i;
}
used[i] = 1;
backtrack(n, idx + 1, buf, used, res);
used[i] = 0;
buf[idx] = 0;
if (i != 1) {
buf[idx + i] = 0;
}
}
}
public:
vector<int> constructDistancedSequence(int n) {
vector<int> buf(2 * n - 1);
vector<int> used(n + 1);
vector<int> res;
backtrack(n, 0, buf, used, res);
return res;
}
};
P7
我们有 n 栋楼,编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节,部分员工想要换一栋楼居住。
给你一个数组 requests ,其中 requests[i] = [fromi, toi] ,表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。
一开始 所有楼都是满的,所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ,一个员工要离开楼 1 ,一个员工要离开楼 2 ,如果该请求列表可行,应该要有两个员工搬入楼 0 ,一个员工搬入楼 1 ,一个员工搬入楼 2 。
请你从原请求列表中选出若干个请求,使得它们是一个可行的请求列表,并返回所有可行列表中最大请求数目。
https://leetcode.cn/problems/maximum-number-of-achievable-transfer-requests/
示例 1:
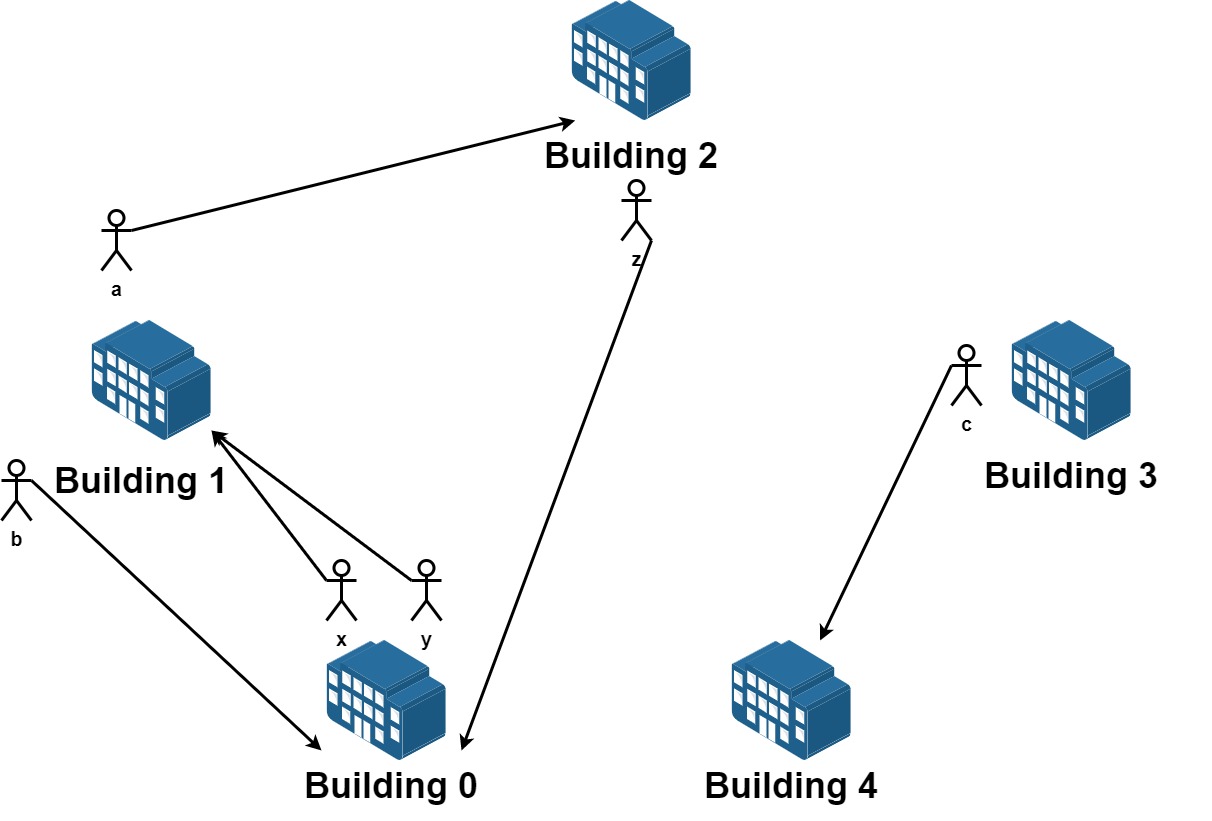
输入:n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出:5
解释:请求列表如下:
从楼 0 离开的员工为 x 和 y ,且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ,且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ,且他想要搬到楼 0 。
从楼 3 离开的员工为 c ,且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼,以满足他们的请求。
我们可以让 y,a 和 z 三人在三栋楼间交换位置,满足他们的要求。
所以最多可以满足 5 个请求。
提示:
1 <= n <= 20
1 <= requests.length <= 16
requests[i].length == 2
0 <= fromi, toi < n
class Solution {
public:
int maximumRequests(int n, vector<vector<int>>& requests) {
int m = requests.size();
int limit = 1 << m;
int res = 0;
vector<int> cnts(n);
for (int i = 0; i < limit; ++i) {
int size = __builtin_popcount(i);
if (size <= res) {
continue;
}
fill(cnts.begin(), cnts.end(), 0);
for (int j = 0; j < m; ++j) {
if ((1 << j) & i) {
--cnts[requests[j][0]];
++cnts[requests[j][1]];
}
}
if (count(cnts.begin(), cnts.end(), 0) == n) {
res = max(res, size);
}
}
return res;
}
};
P8
给你一张 无向 图,图中有 n 个节点,节点编号从 0 到 n - 1 (都包括)。同时给你一个下标从 0 开始的整数数组 values ,其中 values[i] 是第 i 个节点的 价值 。同时给你一个下标从 0 开始的二维整数数组 edges ,其中 edges[j] = [uj, vj, timej] 表示节点 uj 和 vj 之间有一条需要 timej 秒才能通过的无向边。最后,给你一个整数 maxTime 。
合法路径 指的是图中任意一条从节点 0 开始,最终回到节点 0 ,且花费的总时间 不超过 maxTime 秒的一条路径。你可以访问一个节点任意次。一条合法路径的 价值 定义为路径中 不同节点 的价值 之和 (每个节点的价值 至多 算入价值总和中一次)。
请你返回一条合法路径的 最大 价值。
注意:每个节点 至多 有 四条 边与之相连。
https://leetcode.cn/problems/maximum-path-quality-of-a-graph/
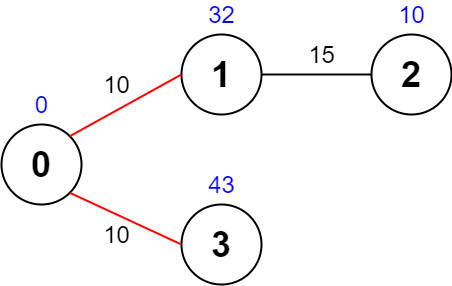
输入:values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
输出:75
解释:
一条可能的路径为:0 -> 1 -> 0 -> 3 -> 0 。总花费时间为 10 + 10 + 10 + 10 = 40 <= 49 。
访问过的节点为 0 ,1 和 3 ,最大路径价值为 0 + 32 + 43 = 75 。
n == values.length
1 <= n <= 1000
0 <= values[i] <= 108
0 <= edges.length <= 2000
edges[j].length == 3
0 <= uj < vj <= n - 1
10 <= timej, maxTime <= 100
[uj, vj] 所有节点对 互不相同 。
每个节点 至多有四条 边。
图可能不连通。
class Solution {
public:
int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {
int n = values.size();
vector<vector<pair<int, int>>> g(n);
for (const auto& edge: edges) {
g[edge[0]].emplace_back(edge[1], edge[2]);
g[edge[1]].emplace_back(edge[0], edge[2]);
}
vector<int> visited(n);
visited[0] = true;
int ans = 0;
function<void(int, int, int)> dfs = [&](int u, int time, int value) {
if (u == 0) {
ans = max(ans, value);
}
for (const auto& [v, dist]: g[u]) {
if (time + dist <= maxTime) {
if (!visited[v]) {
visited[v] = true;
dfs(v, time + dist, value + values[v]);
visited[v] = false;
}
else {
dfs(v, time + dist, value);
}
}
}
};
dfs(0, 0, values[0]);
return ans;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号