网络延迟时间

题目

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

示例 1：

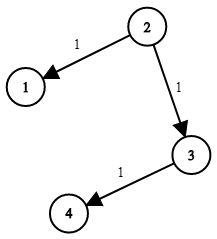
输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2
示例 2：

输入：times = [[1,2,1]], n = 2, k = 1
输出：1
示例 3：

输入：times = [[1,2,1]], n = 2, k = 2
输出：-1

提示：

1 <= k <= n <= 100
1 <= times.length <= 6000
times[i].length == 3
1 <= ui, vi <= n
ui != vi
0 <= wi <= 100
所有 (ui, vi) 对都 互不相同（即，不含重复边）

思路：

一开始是想着用回溯探索的方式去做的，但是会超时，所以用dijstra算法实现

代码

#define dijkstra
#ifdef huisu
class Solution {
private:
    //前面的拓扑排序用的是图的邻接表，两者虽然都是二维矩阵，但是意义是不一样的
    vector<vector<int>> graph;
    int nsize;//表示的是graph实际用得到的大小
    //int timenode[101] = {INT_MAX};//有误，不能这么初始化，这样都变成0了
    int timenode[101];

private:
    void dfs(int k, vector<bool>& used, int time) {
        //遍历的时候有可能很多次遍历到，但是记录最小的一次时间
        timenode[k] = min(timenode[k], time);

        for(int i = 1; i <= nsize; i++) {
            if(graph[k][i] != INT_MAX && used[i] == false) {
                used[i] = true;
                dfs(i, used, time + graph[k][i]);
                used[i] = false;
            }
        }
    }
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        //初始化所有的元素都是无穷大,初始化实际用到的大小
        graph = vector<vector<int>>(101, vector<int>(101, INT_MAX));
        nsize = n;
        for(int i = 0; i < 101; i++) {
            timenode[i] = INT_MAX;
        }
        //将times存进邻接矩阵
        for(auto it : times) {
            graph[it[0]][it[1]] = it[2];
        }

        //从k点开始遍历，这个点标记为已经使用过了
        //used用于树枝去重
        vector<bool> used = vector<bool>(101, false);
        used[k] = true;
        dfs(k, used, 0);

        int ans = -1;
        for(int i = 1; i <= n; i++) {
            if(timenode[i] == INT_MAX) {
                return -1;
            }else {
                cout << timenode[i] << " ";
                ans = max(ans, timenode[i]);
            }
        }
        return ans;
    }
};
#endif


#ifdef dijkstra
class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        //所有的图的题目开始之前先把图存下来,有向带权图，使用邻接矩阵
        vector<vector<int>> graph(n + 1, vector<int>(n + 1, INT_MAX));
        for(auto it : times) {
            graph[it[0]][it[1]] = it[2];
        }

        //从k点到该点的距离
        vector<int> dist(n + 1, INT_MAX);
        dist[k] = 0;

        //是否被标记
        vector<bool> used(n + 1, false);

        //当前循环中正在已经标记好的点
        for(int k = 1; k <= n; k++) {//这里的循环仅仅代表次数
            //距离k最小的点的下标
            int min = INT_MAX, minj;
            //在所有的没有确定标记的点中寻找距离最小的点
            for(int j = 1; j <= n; j++) {
                if(!used[j] && dist[j] < min){
                    minj = j;
                    min = dist[j];
                }
            }

            used[minj] = true;

            for(int i = 1; i <= n; i++) {
                //用minj这个点去更新与其相邻的节点
                if(graph[minj][i] != INT_MAX) {
                    if(dist[minj] + graph[minj][i] < dist[i]) {
                        dist[i] = dist[minj] + graph[minj][i];
                    }
                }
            }
        }
        int ans = -1;
        for(int i = 1; i <= n; i++) {
            ans = max(ans, dist[i]);
        }
        return ans == INT_MAX ? -1 : ans;

    }
};
#endif