01背包详解

记住，最重要的一点就是不管是二维数组还是一维数组，都是要遍历物品之后遍历背包大小，两个都是需要的，在知道一维数组和二维数组的结构之后，最重要的是知道先遍历物品，之后遍历背包的大小

基本信息

物品编号	物品重量	物品价值
0	1	15
1	3	20
2	4	30

二维数组的方法

二维数组的dp的含义：dp[i][j]表示的是在编号0-i的物体中随意装进大小为j背包中，得到的最大的价值

• 初始化操作
  
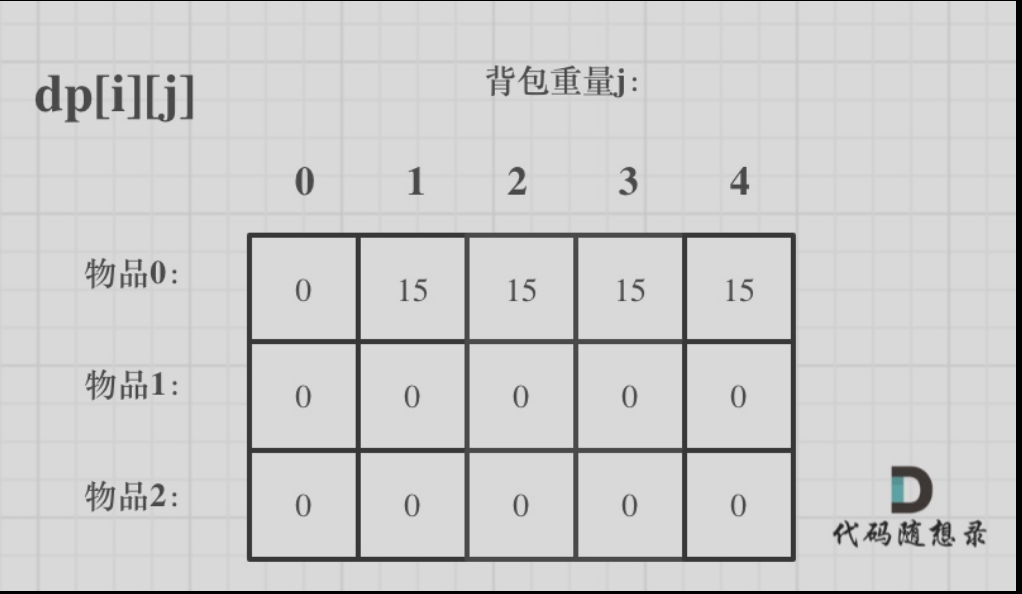
  以上的初始操作是达到一个目的，是为了使得dp[i][j] 呈现以上的效果
  初始化代码：

  // 初始化 dp
  vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
  for (int j = weight[0]; j <= bagweight; j++) {
    dp[0][j] = value[0];
  }
  

• 遍历顺序以及代码
  遍历顺序有两种，但是为了方便理解，我们使用的是先遍历物品，之后遍历背包的大小
  代码：

  /*其中代码判断j < weight[i] 是为了跳过中间间隔的重量
    举一个例子来说就是你的重量是1，3，4，那么合起来的重量就是1，4，5，7
    这样的重量跳转，中间的状态2，3，6只需要继承之前i-1层的价值即可，因为你
    加不进去背包，重量只有到了质变点之后才会改变,也就是加不进去重物了
  */
  for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + 
  value[i]);
  
    }
  }
  

一维数组的方法

一维数组dp的含义： dp[j]表示的是背包大小为j，所装得物体最大的价值是dp[j],
其实就是从二维数组中演变而来，因为我们发现i层都是依赖i-层的状态的，所以我们直接在一层中覆盖原来的数据即可。

• 初始化操作

  dp[0] = 0;//其实只要在构造dp数组得时候全部初始化为零即可
  

• 遍历顺序以及代码
  遍历的时候一定是倒序的，因为如果是正序的话，会出现完全背包的情况，也就是同一个物体被多次放进背包

  for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }