不同的路径Ⅱ

题目

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

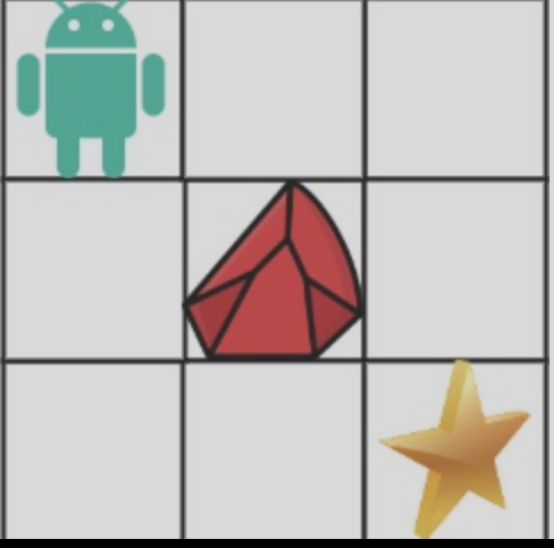
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
   示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

思路

• 确定dp数组的含义，dp[i][j]表示的是到达该坐标的途径有几条

• 递推公式，满足条件obstacleGrid[i][j] == 0 ,
  dp[i][j] = dp[i][j -1] + dp[i - 1][j]
  满足条件obstacleGrid[i][j] == 1，
  dp[i][j] = 0;

• 确定初始条件，要考虑障碍物是不是在边上，要是边界处一点出现障碍物的话那么该点之后的所有的边界点的值都是0

• 确定遍历顺序，遍历顺序是外层按照行数遍历，内层按照列数遍历

• 不用打印中间值

代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        //确定dp数组的含义，dp[i][j]表示的是到达该坐标的途径有几条
        /*递推公式，满足条件obstacleGrid[i][j] == 0 ,
            dp[i][j] = dp[i][j -1] + dp[i - 1][j]
        满足条件obstacleGrid[i][j] == 1，
            dp[i][j] = 0;
        */
        /*确定初始条件，要考虑障碍物是不是在边上，要是边界处一点出现障碍物的话
          那么该点之后的所有的边界点的值都是0
        */
        //确定遍历顺序，遍历顺序是外层按照行数遍历，内层按照列数遍历

        //不用打印中间值
        vector<vector<int>> dp(obstacleGrid);
        vector<vector<int>> dp1(obstacleGrid.size(), vector<int>(obstacleGrid[0].size()));
        //边界初始化
        for(int j = 0; j < obstacleGrid[0].size(); j++) {
            if(obstacleGrid[0][j] == 1) {
                for(; j < obstacleGrid[0].size(); j++) {
                    dp[0][j] = 0;
                }
                break;
            }
            dp[0][j] = 1;
        }
        for(int i = 0; i < obstacleGrid.size(); i++) {
            if(obstacleGrid[i][0] == 1) {
                for(; i < obstacleGrid.size(); i++) {
                    dp[i][0] = 0;
                }
                break;
            }
            dp[i][0] = 1;
        }
        //递推公式
        for(int i = 1; i < obstacleGrid.size(); i++) {
            for(int j = 1; j < obstacleGrid[0].size(); j++) {
                if(obstacleGrid[i][j] == 0) {
                    dp[i][j] = dp[i][j - 1] + dp[i -1][j];
                }else {
                    dp[i][j] = 0;
                }
            }
        }

        return dp[obstacleGrid.size() - 1][obstacleGrid[0].size() - 1];
    }
};