删除二叉搜索树的节点

题目

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:

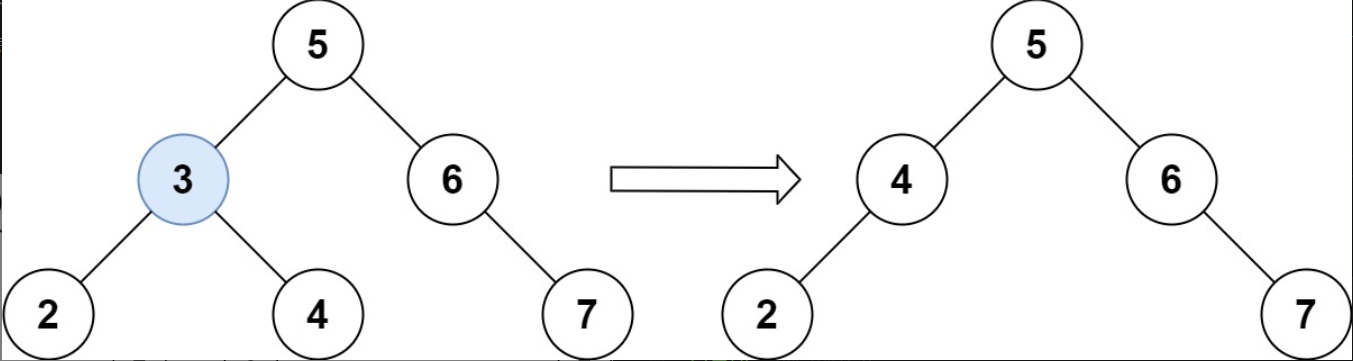
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
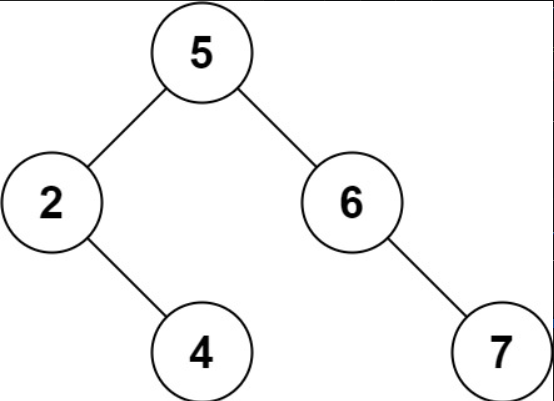
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:

输入: root = [], key = 0
输出: []

提示:

节点数的范围 [0, 104].
-105 <= Node.val <= 105
节点值唯一
root 是合法的二叉搜索树
-105 <= key <= 105

思路

• 首先这是一个二叉搜索树，也就是说每一个节点下一步往哪个方向都是定好了的，其次如果你找到了这个节点，首先二叉搜索树要不用左中右得到的有序数组来解决，要不就是按照每一个节点有大小之分来走，很明显是后者。
• 其次当你找到这个key的时候，又要分为四种情况，
  1. 左右节点都是空的（那直接操作删除这个节点）
  2. 左节点空，右节点不为空（用右节点替换这个节点，并把这节点delete掉）
  3. 左节点不为空，右节点为空（同上）
  4. 左右节点都不为空 （这里的操作是最迷惑的，怎么才能不动前面的所有的节点的情况下安排左右子树的节点，把左子树嫁接到右子树的最左边的节点上是不是就可以了呢）

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* delete_node(TreeNode* cur, int key) {//边删除节点边建立新的树
        if(cur == NULL) {
            return NULL;
        }
        if(cur->val == key){//有很四种情况需要考虑
            //第一种,左右节点都是空的
            if(cur->left == NULL && cur->right == NULL){
                delete cur;
                return NULL;
            }
            //第二种，左节点为空，右节点不为空的
            if(cur->left == NULL && cur->right != NULL){
                return cur-> right;
                delete cur;
            }
            //第三种，右节点为空，左节点不为空的
            if(cur->left != NULL && cur->right == NULL){
                return cur-> left;
                delete cur;
            }
            //第四种，左右节点都不为空(注意这里需要把左子树嫁接到右子树最左边的节点上)
            if(cur->left != NULL && cur->right !=NULL){
                TreeNode* pos = cur->right;
                while(pos->left) {
                    pos = pos->left;
                }
                pos->left = cur->left;
                TreeNode* delNode = cur;
                return cur->right;
                delete delNode;
            }
        }

        if(cur->val > key){
            cur->left = delete_node(cur->left,key);
        }
        if(cur->val < key){
            cur->right = delete_node(cur->right,key);
        }

        return cur;
    }
    TreeNode* deleteNode(TreeNode* root, int key) {
        return delete_node(root,key);
    }
};