二叉搜索树的最小绝对差

题目

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

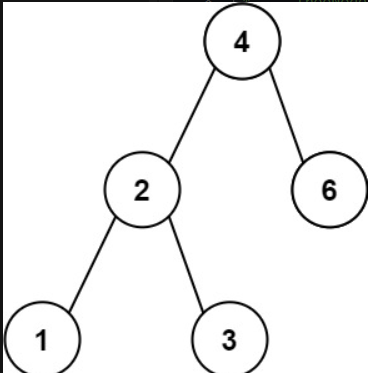
输入：root = [4,2,6,1,3]
输出：1
示例 2：

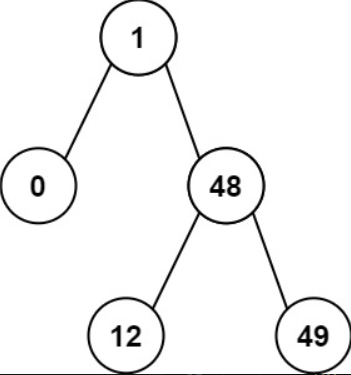
输入：root = [1,0,48,null,null,12,49]
输出：1

思路

做到这个题目的时候我已经可以找到二叉搜索树的题目的一个精髓，那就是一定要注意要以有序数组的角度去看待二叉搜索树，因为有很多时候你按照树的思想去做题目的时候，
会出现一些你很难理解的情况，以这个题目为例，这里的pre指针指代的是哪一个节点，用这个图片来描述最为合适：

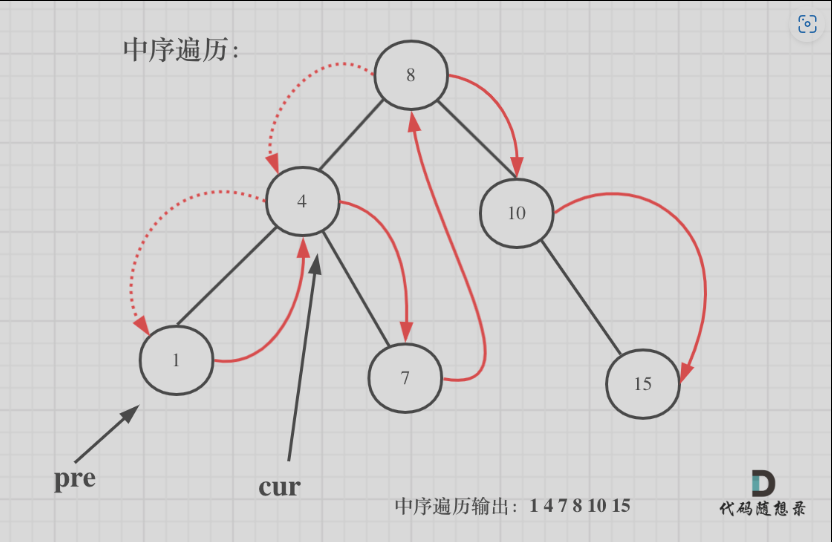
它遍历的顺序是按照实线的方向来进行的，把它张开那就是一个有序数组，所以这个pre代表的是有序数组的上一个节点，可以这么看待

• 以下还有一个错误版本就是把它当作树来理解了

代码

class Solution {
public:
    int result;
    TreeNode* pre;
    void getAnswer(TreeNode* cur) {
        if(cur == NULL) {
            return;
        }
        getAnswer(cur->left);
        if(pre != NULL) {
            result = min(result, abs(pre->val - cur->val));
        }
        pre = cur;
        getAnswer(cur->right);
    }
    int getMinimumDifference(TreeNode* root) {
        result = 1e5;
        pre = NULL;
        getAnswer(root);
        return result;
    }
};
//错误的版本，按照树来理解就会出现问题，那就是没有理解这个相邻节点和把它放到有序数组当中去的时候区别
// class Solution {
// public:
//     int result = INT_MAX;
//     void getMin(TreeNode* cur){
//         if(cur == NULL){
//             return;
//         }
//         if(cur->left == NULL && cur->right == NULL){
//             return;
//         }
//         if(cur->left!=NULL){
//             result = result <= abs(cur->val - cur->left->val)?
//             result : abs(cur->val - cur->left->val);
//         }
//         if(cur->right!=NULL){
//             result = result <= abs(cur->val - cur->right->val)?
//             result : abs(cur->val - cur->right->val);
//         }
//         getMin(cur->left);
//         getMin(cur->right);
//     }
//     int getMinimumDifference(TreeNode* root) {
//         getMin(root);
//         return result;
//     }
// };