验证二叉搜索树

题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

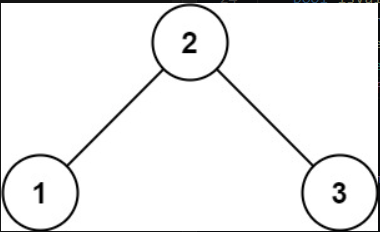
输入：root = [2,1,3]
输出：true
示例 2：

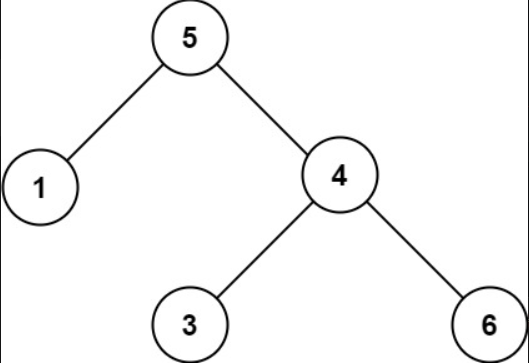
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4

思路

• 两种方法，利用二叉搜索树的特点，中序遍历是有序的
• 使用递归判断的方法,注意该方法还是借鉴了二叉搜索树的特点，也就是中序遍历是有序的

代码

• 中序判断法

  class Solution {
  public:
      vector<int> ve;
      //用中序遍历之后看是不是有序的，这里为了记录迭代的方法，采用循环的方法
      void inorderT(TreeNode* root) {
          stack<TreeNode*> st;
          if(root != NULL) {
              st.push(root);
          }
          //左中右，在cur != NULL中，先弹出之后按照右中左的顺序进栈，中后要带着NULL
          while(!st.empty()) {
              TreeNode* cur = st.top();
              if(cur != NULL) {
                  st.pop();
                  if(cur->right) st.push(cur->right);
                  st.push(cur);
                  st.push(NULL);
                  if(cur->left) st.push(cur->left);
              }else {
                  st.pop();
                  cur = st.top();
                  st.pop();
                  ve.push_back(cur->val);
              }
          }
      }
      bool istrue() {
          for(int i = 1; i < ve.size(); i++) {
              if(ve[i - 1] >= ve[i]) {
                  return false;
              }
          }
          return true;
      }
      bool isValidBST(TreeNode* root) {
          inorderT(root);
          return istrue();
      }
  };
  

• 递归判断法

  class Solution {
  public:
      TreeNode* per;
      bool dfs(TreeNode* cur) {
          if(cur == NULL) {
              return true;
          }
          bool left = dfs(cur->left);
  
          if(per != NULL && per->val >= cur->val) {
              return false;
          }
          per = cur;
          bool right = dfs(cur->right);
          return left && right;
      }
      bool isValidBST(TreeNode* root) {
          per = NULL;
          return dfs(root);
      }
  };