环形链表

题目

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

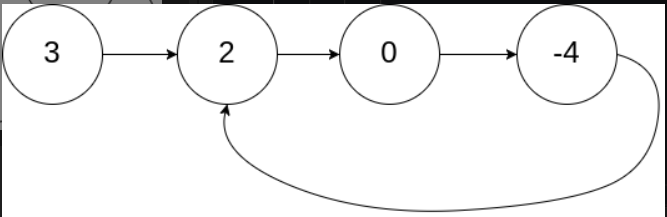
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：

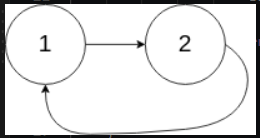
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引

思路

这个思路比较难以想到，需要一定的数学功底，思路就是定义两个指针，一个是fast，一个是slow，两者以两倍的速度前进，如果存在环形的话那么肯定会相遇的，要是没有环的话，那么肯定是不会相遇的，也就是最后返回null，然后寻找这个入环的节点也是一样的，两者有一个数学公式推导，集体的看代码随想录的介绍。

代码

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast!=NULL && fast->next!=NULL){
            slow = slow->next;//slow指针前进一步
            fast = fast->next->next;//fast指针前进两步
            if(fast == slow){//如果相遇的话，开始计算相交的节点
                slow = head;
                while(fast!=slow){
                    fast = fast->next;
                    slow = slow->next;
                }
                return slow;
            }
        }
        return NULL;//最后退出了循环，说明没有环形
    }
};