图的遍历

准备工作

图的结构：

　　//结点集合
    ArrayList<String> nodes;
    //边的个数
    private int edgeNum;
    //邻接矩阵：边是否连通或边之间的权值
    private int[][] weight;
    //记录结点是否被访问过：用于遍历
    private boolean[] visited;

构造器：

　　//构造器
    public Graph(int n) {
        this.nodes = new ArrayList<>(n);
        this.edgeNum = 0;
        this.weight = new int[n][n];
    }

给图添加结点和边：这里默认是无向图

　　 //添加结点
    public void insertNode(String node){
        nodes.add(node);
    }

    //添加边
    public void insertEdge(int v1,int v2,int w){
        weight[v1][v2]=w;
        weight[v2][v1]=w;
        edgeNum++;
    }

显示图对应的邻接矩阵：

 

　　//显示图对应的邻接矩阵
    public void showGraph(){
        for (String val:nodes) {
            System.out.println(val);
        }
    }

 

理解遍历执行过程

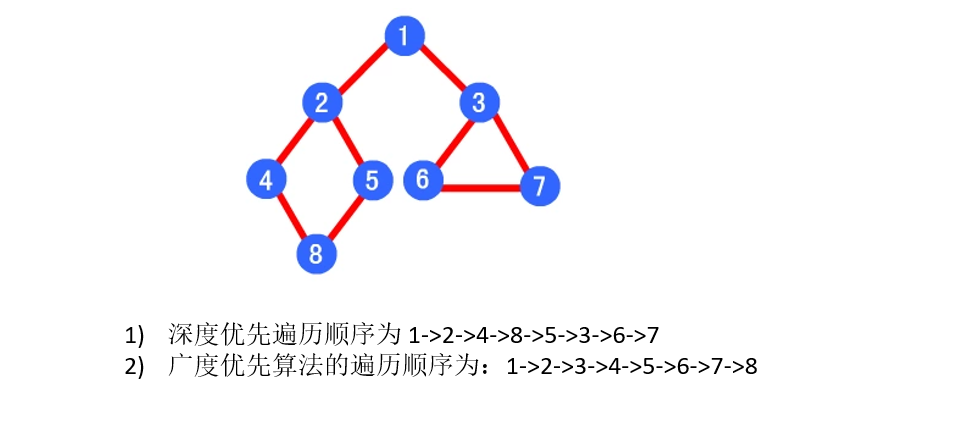
开始遍历算法代码

  1.深度遍历优先

• 特点：深度遍历优先是纵向深挖的遍历，是一种顺着一个结点得到其邻接结点后不断挖掘邻接结点的邻接结点的算法。
• 思路：从图中某个顶点V₀出发，访问该结点，然后从未被访问过的V₀的邻接结点出发，继续深度遍历图中其余结点，直至所有与V₀连通的结点都被遍历过。然后再重新选择一个结点出发，重复上述过程，直至所有结点都被遍历过。
• 代码：

  //深度优先搜索
      public void dfs(){
          int size = nodes.size();
          visited=new boolean[size];
          //便于遍历完一个结点的所有邻接结点后，重新选择结点
          for (int i = 0; i < size; i++) {
              if (!visited[i]){
                  dfs(i);
              }
          }
      }
  
      /**
       * 获取当前结点的所有连通结点
       * @param i 当前结点的下标
       */
      private void dfs(int i) {
          //从当前结点出发
          System.out.print(nodes.get(i)+" ");
          visited[i]=true;
          //获取当前结点的邻接结点
          int neighbor = getFirstNeighbor(i);
          //下面的这个循环是核心所在
          //如果邻接结点未被访问过，则继续访问邻接结点的邻接结点；否则，回溯到上一层，重新选择邻接结点。直到遍历完所有与当前结点连通的结点。
          while (neighbor!=-1){
              if (!visited[neighbor]){
                  dfs(neighbor);
              }else { //在这里实现当前结点的第二、三...个直接邻接结点进行深度遍历 
                  neighbor=getNextNeighbor(i,neighbor);
              }
          }
  
      }
  
      /**
       * 获得当前结点的第一个邻接结点
       * @param index 当前结点对应的下标
       * @return 如果当前结点有邻接结点，则返回第一个找到的邻接结点的下标；否则，返回-1.
       */
      private int getFirstNeighbor(int index) {
          for (int j = 0; j < nodes.size(); j++) {
              if (weight[index][j]>0){
                  return j;
              }
          }
          return -1;
      }
  
      /**
       *
       * @param v1 当前结点
       * @param v2 当前结点已经访问过的相邻接点
       * @return 返回剩下的当前结点尚未访问过的相邻接点中的第一个的下标；如果当前结点没有尚未访问过的相邻接点，则返回-1。
       */
      public int getNextNeighbor(int v1,int v2) {
          for (int i = v2+1; i < nodes.size(); i++) {
              if (weight[v1][i]>0){
                  return i;
              }
          }
          return -1;
      }

   

• 重新整理思路：
  1. 选择一个未被访问过的结点，出发；
  2. 访问当前结点，然后访问当前结点的第一个邻接结点，并深度遍历该结点的所有邻接结点，然后访问当前结点的第二个邻接结点并深度遍历该结点的所有结点...直至当前结点的所有邻接结点都被访问过。此时，与当前结点连通的所有结点都被访问完；
  3. 重复1,2步，直至所有结点都被访问过。

  2.广度优先搜索

• 特点：广度遍历优先是横向的遍历，是一种类似于树的层级遍历的算法。
• 思路：从图中的某个结点V₀出发，访问该结点的邻接结点，然后按照访问邻接结点的顺序依次访问这些邻接结点的邻接结点，直至图中所有和V₀连通的结点都被访问到。然后重新选取一个未被访问过的结点重复上述过程。
• 代码：

  　　//广度优先搜索
      public void bfs(){
          int size = nodes.size();
          visited=new boolean[size];
          //便于访问完一个连通子图后，可以重新选择出发结点
          for (int i = 0; i < nodes.size(); i++) {
              if (!visited[i]){
                  bfs(i);
              }
          }
      }
  
      /**
       * 获取当前结点的所有连通结点（广度遍历）
       * @param i 出发结点（当前结点）的下标
       */
      private void bfs(int i) {
          //准备
          LinkedList<Integer> queue=new LinkedList<>();
          //访问当前结点
          System.out.print(nodes.get(i)+" ");
          visited[i]=true;
          queue.add(i);
          //遍历当前结点的所有连通结点
          while (!queue.isEmpty()){
              //从队列中取出一个结点，开始某个结点的新的一层的遍历
              int curr = queue.removeFirst();
              //遍历一层：获取取出结点的所有直接相邻结点
              int neighbor = getFirstNeighbor(curr);
              while (neighbor!=-1){
                  if (!visited[neighbor]) {
                      System.out.print(nodes.get(neighbor)+" ");
                      visited[neighbor]=true;
                      queue.add(i);
                  }
                  neighbor=getNextNeighbor(curr,neighbor);
              }
          }
      }
  
  　　/**
       * 获得当前结点的第一个邻接结点
       * @param index 当前结点对应的下标
       * @return 如果当前结点有邻接结点，则返回第一个找到的邻接结点的下标；否则，返回-1.
       */
      private int getFirstNeighbor(int index) {
          for (int j = 0; j < nodes.size(); j++) {
              if (weight[index][j]>0){
                  return j;
              }
          }
          return -1;
      }
  
      /**
       *
       * @param v1 当前结点
       * @param v2 当前结点已经访问过的相邻接点
       * @return 返回剩下的当前结点尚未访问过的相邻接点中的第一个的下标；如果当前结点没有尚未访问过的相邻接点，则返回-1。
       */
      public int getNextNeighbor(int v1,int v2) {
          for (int i = v2+1; i < nodes.size(); i++) {
              if (weight[v1][i]>0){
                  return i;
              }
          }
          return -1;
      }

   

• 重新整理思路：
  1. 选择一个未被访问过的结点，出发；
  2. 访问当前结点，然后访问当前结点的第一个邻接结点，第二个邻接结点...直至访问完当前结点的所有直接邻接结点。此时，当前结点的直接子层结点访问完毕；
  3. 依次选择上一层访问过的结点，访问其直接相邻结点，直至访问完所有的上一层结点的直接相邻结点。此时，访问完当前结点的第二层结点；
  4. 重复3，访问完当前结点的第三层结点...直至访问完当前结点的所有连通结点；
  5. 重新选择有一个未被访问过的结点出发，重复1,2,3,4步来完成一个结点的子图的广度遍历。