数据结构之二叉树

一、概述

1.树的基本定义

树是由n（n>=1）个有限结点构成的一个具有层次关系的集合。之所以叫做“树”，是因为看起来像是一颗倒挂的、根在上叶在下的树。

 

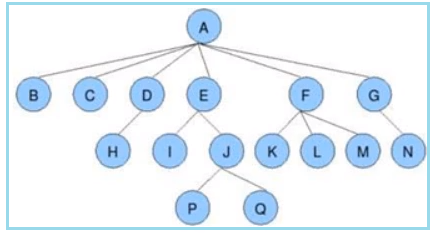
树具有如下特征：

　　没有父结点的结点为根结点；

　　没有子结点的结点为叶节点；

　　每个非根结点有且仅有一个父结点；

　　每个结点有零或多个子结点；

2.树的相关术语

• 孩子结点：一个结点的直接后继结点称为该结点的孩子结点。
• 双亲结点(父结点)：一个结点的直接前驱称为该结点的双亲结点。
• 兄弟结点：同一双亲结点的孩子结点间互称兄弟结点。
• 叶结点：度为0的结点称为叶结点，也可以叫做终端结点
• 分支结点：度不为0的结点称为分支结点，也可以叫做非终端结点

 

• 结点的度：一个结点含有的子树的个数称为该结点的度。
• 树的度：树中所有结点的度的最大值。
• 结点的层次：从根结点开始，根结点的层次为1，根的直接后继层次为2，以此类推。
• 树的高度(深度)：树中结点的最大层次。
• 结点的层序编号：将树中的结点，按照从上层到下层，同层从左到右的次序排成一个线性序列，把他们编成连续的自然数。
• 森林：m（m>=0）个互不相交的树的集合，将一颗非空树的根结点删去，树就变成一个森林；给森林增加一个统一的根结点，森林就变成一棵树。

3.二叉树的分类

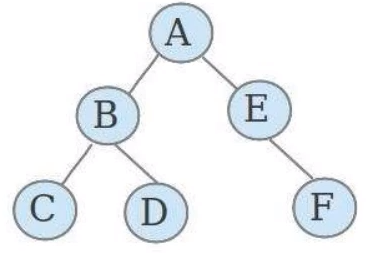
• 二叉树：就是度不超过 2的树(每个结点最多有两个子结点)。

　　

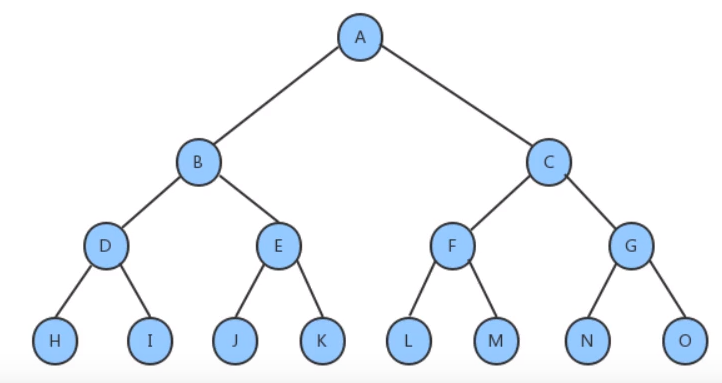
• 满二叉树：一个二叉树，如果每一个层的结点树都达到最大值，则这个二叉树就是满二叉树。

　　

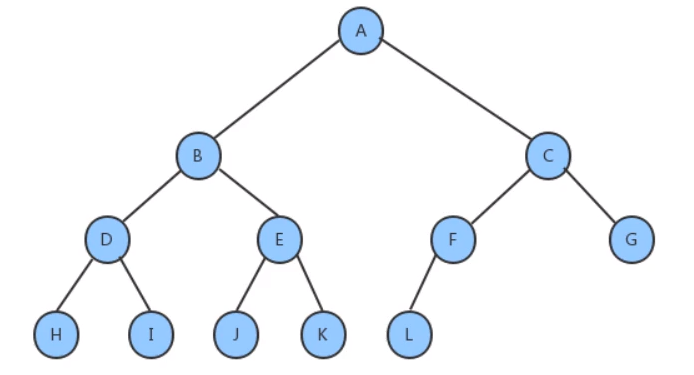
• 完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。

　　

 

二、二叉查找树的实现

1.基本功能：添加、获取、删除

• 结构：可以用链表或线性表，下面以取链表为例。Node类的成员变量包括键值对的key和value，以及左孩子结点和右孩子结点。

• 特点：对于每一个子树，左子树的元素都小于其根结点，右子树的元素都大于其根结点。
• 实现思路：
  • 插入元素：
    • 有返回值递归版：从根结点开始。如果是往空子树中插入，只需创建新结点返回即可，上层会将返回的新结点设为根结点；如果是往非空子树中插入，就需要根据key值的大小选择左子树或右子树进行递归遍历，并将添加元素后的新左/右子树赋值给原左/右子树。即，会统一遍历到空结点，在这里创建N++和结点结束返回。
    • 无返回值重复调用版：分为两种情况，一种是往空子树中插入，创建新结点设为根结点即可，一种是往非空子树中插入，根据key的大小选择左子树或右子树往下深入遍历，自行负责创建结点和结点数增加。
  • 获取元素：遍历获取返回。
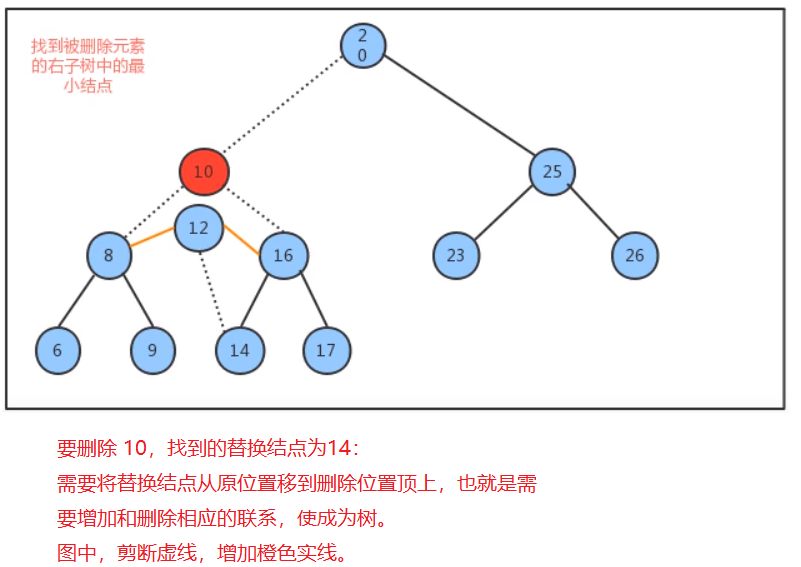
  • 删除元素：如果是删除的叶结点好说，但如果删除的是一个中间结点，那树就会散架成为森林，因此需要一个替换结点来代替删除结点的位置，此结点比较合适的就是比删除结点大一点的，也就是右子树的最左节点。过程如图。

　　　　　　

• 代码实现：

  package com.ex.tree;
  
  /**
   * 实现二叉查找树
   */
  public class BinaryTree<K extends Comparable<K>,V> {
      //根结点
      private Node root;
      //元素个数
      private int N;
  
      private class Node {
          //键
          private K key;
          //值
          private V value;
          //左孩子
          private Node left;
          //右孩子
          private Node right;
  
          public Node(K key, V value, Node left, Node right) {
              this.key = key;
              this.value = value;
              this.left = left;
              this.right = right;
          }
      }
  
      public BinaryTree() {
      }
  
      //获取树中元素的个数
      public int size(){
          return N;
      }
  
      //向树中插入一个键值对
      public void put(K key,V value){
          root = put(root,key,value);
      }
  
      //给指定树x上，插入一个键值对，并返回添加后的以x为根节点的新树
      private Node put(Node x,K key,V value){
          //如果树为空：
          if (x==null){
              N++;
              return new Node(key,value,null,null);
          }
          //如果树不为空：
          int comp = key.compareTo(x.key);
          if (comp>0){
              //如果key大于x的key，继续搜寻右子树
              x.right = put(x.right,key,value);
          }else if (comp<0){
              //如果key小于x的key，继续搜寻左子树
              x.left = put(x.left,key,value);
          }else {
              //如果key等于x的key，直接替换该结点value
              x.value=value;
          }
          return x;
      }
  
      //根据key，从树中找出对应结点，返回value
      public V get(K key){
          return get(root,key);
      }
  
      //从指定的树x中，找出key对应的value
      private V get(Node x,K key){
          //如果树为空：
          if (x==null){
              return null;
          }
          //如果树不为空：
          int comp = key.compareTo(x.key);
          if (comp>0){
              //如果key大于x的key，继续搜寻右子树
              return get(x.right,key);
          }else if (comp<0){
              //如果key小于x的key，继续搜寻左子树
              return get(x.left,key);
          }else {
              //如果key等于x的key，直接替换该结点value
              return x.value;
          }
      }
  
      //根据key，从树中删除对应的键值对
      public void delete(K key){
          root = delete(root, key);
      }
  
      //根据key，从指定的树中删除对应的键值对
      private Node delete(Node x,K key){
          //如果树为空：
          if (x==null){
              return null;
          }
          //如果树不为空：
          int comp = key.compareTo(x.key);
          if (comp>0){
              //如果key大于x的key，继续搜寻右子树
              x.right = delete(x.right,key);
          }else if (comp<0){
              //如果key小于x的key，继续搜寻左子树
              x.left = delete(x.left,key);
          }else {
              //如果key等于x的key，则进行删除操作：要删除的结点为x
              //结点数-1
              N--;
              //1.如果当前结点的左子树不存在
              if (x.left ==null){
                  return x.right;
              }
              //2.如果当前结点的右子树不存在
              if (x.right ==null){
                  return x.left;
              }
              //3.如果当前结点的左右子树都存在
              //3.1找到替换结点（右子树中最小的结点）和其父结点
              Node replaceParNode=x.right;
              while (replaceParNode.left != null && replaceParNode.left.left != null){
                  replaceParNode=replaceParNode.left;
              }
              Node replaceNode=(replaceParNode.left==null)?replaceParNode:replaceParNode.left;
              //3.2断开替换结点和父结点的联系
              replaceParNode.left=null;
              //3.3连接替换结点和删除的父结点、左孩子、右孩子
              replaceNode.left=x.left;
              replaceNode.right=x.right;
              //3.4**断开删除结点和关联结点的联系
              x=replaceNode;
          }
          return x;
  
      }
  
  
  }
  
  

     //向树中插入一个键值对
      public void put(K key,V value){
          put(root,key,value);
      }
  
      //给指定树x上，插入一个键值对，并返回添加后的以x为根节点的新树
      //无返回值重复调用版
      private void put(Node x,K key,V value){
          //如果树为空：
          if (root==null){
              N++;
              root =new  Node(key,value,null,null);
              return;
          }
          //如果树不为空：
          int comp = key.compareTo(x.key);
          if (comp>0){
              //如果key大于x的key，继续搜寻右子树
              if (x.right != null) {
                  put(x.right,key,value);
              }else {
                  x.right=new Node(key,value,null,null);
                  N++;
              }
          }else if (comp<0){
              //如果key小于x的key，继续搜寻左子树
              if (x.left != null) {
                  put(x.left,key,value);
              }else {
                  x.left=new Node(key,value,null,null);
                  N++;
              }
          }else {
              //如果key等于x的key，直接替换该结点value
              x.value=value;
          }
  
  
      }    

   

2.扩展功能：

  2.1查找二叉树中最大/小的键

   //找出整个树最小的键
    public K getMinKey(){
        return getMinKey(root).key;
    }

    private Node getMinKey(Node n) {
        if (n.left!=null){
            return getMinKey(n.left);
        }else {
            return n;
        }
    }

    //找出整个树中最大的键
    public K getMaxKey(){
        return getMaxKey(root).key;
    }

    private Node getMaxKey(Node n) {
        if (n.right!=null){
            return getMaxKey(n.right);
        }else {
            return n;
        }
    }

 

  2.2获取二叉树的最大深度

 

//获取树的最大深度
    public int getMaxDepth(){
        return getMaxDepth(root);
    }

    private int getMaxDepth(Node n) {
        //1.如果根结点为空：则最大深度为0
        if (n==null){
            return 0;
        }
        //2.如果根结点不为空：
        //设变量分别保存树、左子树、右子树的最大深度
        int max=0,maxL=0,maxR=0;
        //2.1如果左子树不为空，则计算左子树的最大深度
        if (n.left != null){
            maxL = getMaxDepth(n.left);
        }
        //2.2如果右子树不为空，则计算右子树的最大深度
        if (n.right != null) {
            maxR = getMaxDepth(n.right);
        }
        //2.3计算树树的最大深度：左右子树中的较大者+1
        max = maxL>maxR?maxL+1:maxR+1;
        return max;

    }

 

 

3.基础遍历

　　

 

 

 

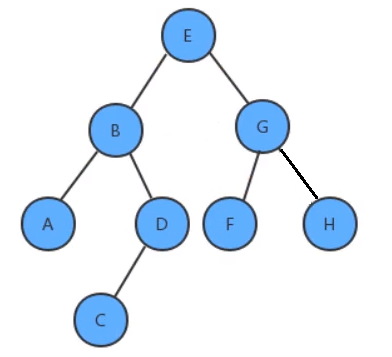
　　3.1前序遍历：先访问根结点，然后再访问左子树，最后访问右子树

　　前序遍历结果：EBADCGFH

　　3.2中序遍历：先访问左子树，中间访问根节点，最后访问右子树

　　中序遍历结果：ABCDEFGH

　　3.3后序遍历：先访问左子树，再访问右子树，最后访问根节点

　　后序遍历结果：ACDBFHGE

 

　　3.4层序遍历：从根节点（第一层）开始，依次向下，获取每一层所有结点的值

　　层序遍历结果：EBGADFHC

 

　　实现代码：

//前序遍历，获得整个树中所有的键
    public Queue<K> preOrderTraversal(){
        Queue<K> keys=new LinkedList<>();
        preOrderTraversal(root, keys);
        return keys;
    }

    private void preOrderTraversal(Node n, Queue<K> keys) {
       if (n!=null){
           keys.add(n.key);
           preOrderTraversal(n.left,keys);
           preOrderTraversal(n.right,keys);
       }
    }

    //中序遍历，获得整个树中所有的键
    public Queue<K> middleOrderTraversal(){
        Queue<K> keys=new LinkedList<>();
        middleOrderTraversal(root, keys);
        return keys;
    }

    private void middleOrderTraversal(Node n, Queue<K> keys) {
        if (n!=null){
            middleOrderTraversal(n.left,keys);
            keys.add(n.key);
            middleOrderTraversal(n.right,keys);
        }
    }

    //后序遍历，获得整个树中所有的键
    public Queue<K> postOrderTraversal(){
        Queue<K> keys=new LinkedList<>();
        postOrderTraversal(root, keys);
        return keys;
    }

    private void postOrderTraversal(Node n, Queue<K> keys) {
        if (n!=null){
            postOrderTraversal(n.left,keys);
            postOrderTraversal(n.right,keys);
            keys.add(n.key);
        }
    }

    //层序遍历，获得整个树中所有的键
    public Queue<K> layerTraversal(){
        Queue<K> keys=new LinkedList<>();
        //创建队列，存储每一层的结点
        Queue<Node> queue=new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            //出队一个元素
            Node node = queue.poll();
            //2.获取当前结点的key；
            keys.offer(node.key);
            //如果当前结点的左子结点不为空，则把左子结点放入到队列中
            if (node.left!=null){
                queue.offer(node.left);
            }
            //如果当前结点的右子结点不为空，则把右子结点放入到队列中
            if (node.right!=null){
                queue.offer(node.right);
            }
        }
        return keys;
    }