一、概述
- 链表:链表是一种物理存储结构上非连续非顺序的存储结构,其物理结构不能直观地表示其逻辑结构,链表的逻辑结构是通过结点的指针域连接起来的。链表由一系列的结点组成,结点由选择的操作动态生成。
- 特点:增删快、查询慢(因为无法直接索引访问,要遍历查找)
二、链表实现
0.编写前需知
- 下面的类中的对 Iterable 接口的实现和 LIterator 内部类的编写是为了使该链表可以用foreach遍历访问,不是必需的。
- 元素:数据。 注意,元素≠结点,结点还包括首结点这种没有存储数据的辅助结点。元素数量同样不包括首结点。
- 方法参数的 位置i 指的都是索引位置,在链表中,索引0从首结点后面的结点开始计数。对下面方法参数里的“位置i的元素”的理解:索引从0开始,head.next为首元素,执行i次,得到索引为i的元素。
1.单向链表

- 结构:Node类的成员变量包括 数据域item 和 指向下一个结点的指针域next,单向链表类LinkList的成员变量包括首结点head和元素数量N。
- 特点:只能单向访问,查找元素的时候只可以从头遍历。
- 代码实现:
package com.ex.link; import java.util.Iterator; /** * 实现单向链表 */ public class LinkList<T> implements Iterable<T>{ //头结点 private Node head; //元素数量 private int N; private class Node{ //数据域,存放数据 T item; //指针域,指向下一个节点 Node next; public Node(T item,Node next) { this.item = item; this.next = next; } } //构造函数 public LinkList() { this.head=new Node(null,null); this.N=0; } //在链表中添加一个节点 public void insert(T t){ //获取尾结点 Node n=head; while (n.next!=null){ n=n.next; } //创建新结点 Node newNode = new Node(t, null); //尾结点指向新结点 n.next=newNode; //结点数+1 N++; } //向链表的i位置元素之前添加一个节点 public void insert(T t,int i){ //找到i-1位置元素 Node pre=head.next; for (int j = 0; j < i - 1; j++) { pre=pre.next; } //找到i位置元素 Node curr=pre.next; //新建新结点 //新结点的指针域指向i位置元素,i-1 // 位置元素指向新结点 Node newNode = new Node(t, curr); pre.next=newNode; //结点数+1 N++; } //获取链表的i位置元素并返回 public T get(int i){ Node n=head.next; for (int j = 0; j < i; j++) { n=n.next; } return n.item; } //获取链表中首次出现的指定元素的位序号,若不存在,则返回-1 public int indexOf(T t){ //一边比较一边后移,找到指定元素 或 指针已经挪到尾结点为结束 Node n=head; for (int i=0;n.next != null;i++){ n=n.next; if (n.item.equals(t)) { return i; } } return -1; } //清空链表 public void clear(){ //将首结点的指针域置null head.next=null; //结点数置0 N=0; } //删除i位置元素 public T remove(int i){ //找到i-1位置元素 Node pre=head.next; for (int j = 0; j < i - 1; j++) { pre=pre.next; } //找到i位置元素 Node curr=pre.next; //将i-1位置元素的指针域指向第i+1个元素 pre.next=curr.next; //节点数-1 N--; //返回删除的元素 return curr.item; } //获取链表的长度 public int length(){ return N; } //判断链表是否为空,是则返回true,否则返回false public boolean isEmpty(){ return N==0; } //以下方法和类均为了实现遍历 @Override public Iterator<T> iterator() { return new LIterator(); } private class LIterator implements Iterator<T>{ private Node n; public LIterator() { this.n = head; } @Override public boolean hasNext() { return n.next!=null; } @Override public T next() { n=n.next; return n.item; } } }
 View Code
View Codepackage com.ex.link; public class LinkListTest { public static void main(String[] args) { LinkList<Integer> list = new LinkList<>(); //测试插入方法 list.insert(1); list.insert(2); list.insert(3); list.insert(4); for (Integer val:list) { System.out.println(val); } System.out.println("-------------"); //测试插入指定位置 list.insert(55,2); for (Integer val:list) { System.out.println(val); } System.out.println("-------------"); //测试删除元素 list.remove(1); for (Integer val:list) { System.out.println(val); } System.out.println("-------------"); //测试获取元素 System.out.println(list.get(2)); //测试indexOf System.out.println(list.indexOf(1)); } }
2.双向链表

- 结构:Node类的成员变量包括数据域item、指向前驱结点的指针域pre、指向后继结点的指针域next,双向链表类的成员变量包括首结点head、尾结点tail、元素数量N。
- 特点:可以双向访问,查找元素既可以从头开始也可以从尾开始,查找元素可进可退,便于查找倒数第N个元素。但需要多分配一个指针存储空间,且增删元素复杂。
- 代码实现:
package com.ex.link; import java.util.Iterator; /** * 实现双向链表 * 对下面方法参数里的“位置i的元素”的理解: * 索引从0开始,head.next为首元素,执行i次,得到索引为i的元素 * */ public class TwoWayLinkList<T> implements Iterable<T>{ //头结点 private Node head; //尾结点 private Node tail; //元素数量 private int N; private class Node { //数据域 T item; //指向前驱结点的指针域 Node pre; //指向后继结点的指针域 Node next; public Node(T item, Node pre, Node next) { this.item = item; this.pre = pre; this.next = next; } } //构造函数 public TwoWayLinkList() { //初始时,只有头结点: //头结点 this.head=new Node(null,null,null); //尾结点 this.tail=null; //节点个数 this.N=0; } //添加一个元素 public void insert(T t){ if (isEmpty()){ //如果链表为空: //构造新结点 Node newNode = new Node(t, head, null); //头结点指向新结点 head.next=newNode; //新结点成为尾结点 tail=newNode; }else { //如果链表不为空: //构造新结点 Node newNode = new Node(t, tail, null); //尾结点指向新结点 tail.next=newNode; //新结点成为尾结点 tail=newNode; } //结点数+1 N++; } //在链表的i位置元素前添加一个元素 public void insert(T t,int i){ //如果没有i位置元素: if (N<i+1) throw new IndexOutOfBoundsException(); //如果有i位置元素: //找到i-1位置结点 Node preNode=head.next; for (int j = 0; j < i - 1; j++) { preNode=preNode.next; } //找到i位置元素 Node curr=preNode.next; //构造新结点 Node newNode = new Node(t, preNode, curr); //令i-1位置元素指向新结点 preNode.next=newNode; //令新结点指向i位置元素 newNode.next=curr; //结点数+1 N++; } //删除并返回链表中的i位置元素 public T remove(int i){ //如果没有i位置元素: if (N<i+1) throw new IndexOutOfBoundsException(); //如果有i位置元素: //找到i-1位置元素 Node preNode=head.next; for (int j = 0; j < i - 1; j++) { preNode=preNode.next; } //找到i位置元素 Node curr=preNode.next; //找到i+1位置元素 Node nextNode=curr.next; //令i-1位置元素指向i+1位置元素 preNode.next=nextNode; //令i+1位置元素指向i-1位置元素 nextNode.pre=preNode; //返回被删除元素 return curr.item; } //清空链表 public void clear(){ //头结点 this.head.next=null; //尾结点 this.tail=null; //结点个数 this.N=0; } //获取链表的i位置元素 public T get(int i){ Node n=head.next; for (int j = 0; j < i; j++) { n=n.next; } return n.item; } //获取第一个元素 public T getFirst(){ if (!isEmpty()){ //如果链表不为空: return head.next.item; }else { //如果链表为空: return null; } } //获取最后一个元素 public T getLast(){ if (!isEmpty()){ //如果链表不为空: return tail.item; }else { //如果链表为空: return null; } } //找到元素在链表中第一次出现的位置 public int indexOf(T t){ //一边移动指针一边比较,结束条件为 已经到了尾结点 或 找到该元素 //因为是先移动后比较,所以从head开始。注意索引和元素的对应。 Node n=head; for (int i=0;n.next != null;i++){ n=n.next; if (n.item.equals(t)){ return i; } } return -1; } //判断链表是否为空,是则返回true,否则返回false public boolean isEmpty(){ return N==0; } //获取并返回链表长度 public int length(){ return N; } //以下方法和类均为了实现遍历 @Override public Iterator<T> iterator() { return new TIterator(); } private class TIterator implements Iterator{ private Node n; public TIterator() { this.n = head; } @Override public boolean hasNext() { return n.next != null; } @Override public Object next() { n=n.next; return n.item; } } }
 View Code
View Codepackage com.ex.link; public class TwoWayLinkListTest { public static void main(String[] args) { TwoWayLinkList<Integer> list = new TwoWayLinkList(); //测试添加元素 list.insert(21); list.insert(22); list.insert(23); list.insert(23); list.insert(24); //测试指定位置添加元素 list.insert(99,3); //遍历链表 for (Integer val:list) { System.out.println(val); } System.out.println("----------"); //测试获取元素 System.out.println("get 5:"+list.get(5)); //测试删除元素 list.remove(0); //测试获取第一个元素 System.out.println("get first:"+list.getFirst()); //测试获取最后一个元素 System.out.println("get last:"+list.getLast()); System.out.println("----------"); for (Integer val:list) { System.out.println(val); } //测试indexOf System.out.println("23:"+list.indexOf(23)); } }
3.循环链表

- 结构:因为链表结点数量不定,且一旦闭环就无法再做修改,因为我将不再特地提前抽象出一个循环链表类,而是只编写一个Node的内部类,在使用时创建循环链表。
- 代码实现:
package com.ex.link; public class CircleTest { public static void main(String[] args) { //创建结点 Node<String> first = new Node<String>("aa", null); Node<String> second = new Node<String>("bb", null); Node<String> third = new Node<String>("cc", null); Node<String> fourth = new Node<String>("dd", null); Node<String> fifth = new Node<String>("ee", null); Node<String> six = new Node<String>("ff", null); Node<String> seven = new Node<String>("gg", null); //完成结点之间的指向 first.next = second; second.next = third; third.next = fourth; fourth.next = fifth; fifth.next = six; six.next = seven; //闭环 seven.next=first; } private static class Node<T> { T item; Node next; public Node(T item, Node next) { this.item = item; this.next = next; } } }
三、链表与顺序表的比较
- 顺序表:
- 方法:get(int i)只需直接根据索引从数组中取元素即可,时间复杂度为O(1);insert(int i,T t)需要将i位置及后面的元素移动一位,随着元素量的增大,需要移动的元素也会增多,时间复杂度为O(n);remove(int i)需要将位置i后面的元素都往前移动一位随着元素量的增大,需要移动的元素也会增多,时间复杂度为O(n)。
- 总结:由于顺序表的底层是数组,会涉及到扩容机制,在当前长度范围内还好,一旦需要扩容,耗时就会突增,数据越多越明显。
- 关键词:查找块、增删慢、需预设长度需扩容。
- 链表:
- 方法:get(int i)需要从头遍历,依次向后查找,时间复杂度为O(n);insert(int i,T t)也需要从头遍历先找到 i-1 位置的元素,才能完成插入,时间复杂度为O(n);删除同样,时间复杂度为O(n)。
- 总结:相较于顺序表,链表的插入和删除操作的时间复杂度虽然也是O(n),但是链表无需连续的物理空间,不需要预设长度,无需扩容,同时插入删除数据也不需要交换数据,因此链表插入和删除操作的性能还是高于顺序表。
- 关键词:查找慢、增删快、无需预设长度无需扩容。
四、链表操作
1.单链表反转
- 思想:
- 将链表看做两部分,一是原链表,也就是没有逆转的链表,二是逆转后的链表,我叫它逆转队列。
- 每个结点都做这样两件事:一是获取当前逆转队列,然后将当前结点和逆转队列连接起来(是否是尾结点只影响连接的是逆转队列还是头结点),二是返回当前结点(也就是当前逆转队列)。
- 图解:
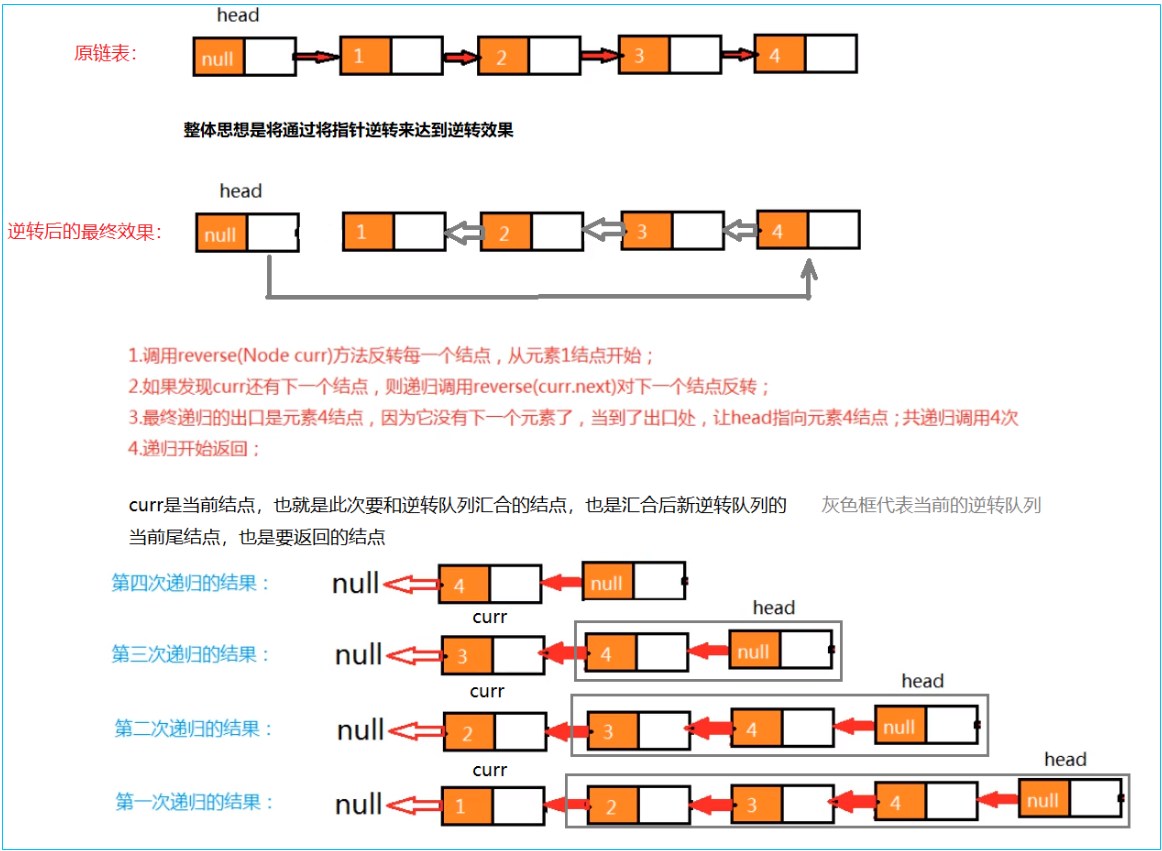
- 实现代码:
//逆转链表 public void reverse(){ //如果链表非空,就进行逆转,否则直接结束运行 if (isEmpty()){ return; } reverse(head.next); } //逆转指定结点,并把逆转后的结点返回 public Node reverse(Node curr){ if (curr.next == null){ //如果是尾结点,就让头结点指向该节点 head.next=curr; return curr; } //如果不是尾结点,就让返回结果指向当前结点 //递归反转的当前结点的下一个结点的返回值就是反转后的当前结点的上一个结点 Node node = reverse(curr.next); node.next=curr; curr.next=null; return curr; }
2.快慢指针
快慢指针:快慢指针指的是定义两个指针,这两个指针的移动速度一块一慢,以此来制造出自己想要的差值,这个差值可以然我们找到链表上相应的结点。一般情况下,快指针的移动步长为慢指针的两倍。
2.1中间值问题
- 题目:获取单向链表的中间节点的值。
- 思路:设置一个慢指针一个快指针,最开始都指向首元素结点,快指针的移动速度是慢指针的2倍,当快指针移动到链表末尾时,慢指针正好移动到链表中间。
- 代码实现:
//查找中间值 public T getMid(){ //定义快慢指针 Node slow=head.next,fast=head.next; //移动快慢指针,当快指针指向尾结点(元素个数为偶数)或 尾结点后的null(元素个数为奇数) 时结束 while (fast!=null && fast.next!=null) {//注意条件和子条件的顺序,要先判断fast再判断fast.next //移动快慢指针 slow=slow.next; fast=fast.next.next; } //返回慢指针对应节点的数据作为中间值 return slow.item; }
2.2判断单向链表是否有环问题 及 有环链表入口问题
注:上面编写的单向链表类LinkList将Node类设置为私有内部类,外部即LinkList类之外无法访问到指针域next,因此无法设置环,不可能有环。
因此以下两个“环”问题采用的不是上面的LinkList类作为单链表,而是自行连接其N个Node对象作为单链表,并且将Node类设置为和主方法所在类的内部类(也可以不和主方法在一个类,只要去掉Node类的 私有权限即可),以便于访问next域设置环。
- 题目:判断一个单向链表是否有环,如下图所示。
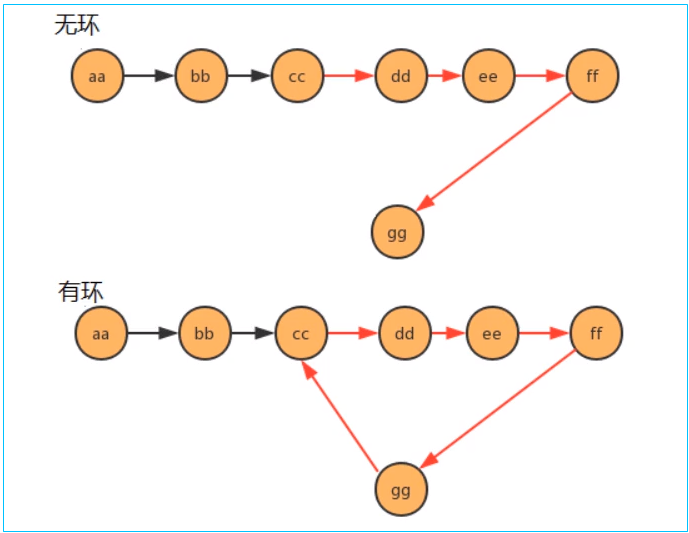
- 思路:设置快慢指针,因为快指针和慢指针之间存在速度差,因此如果有环的话,快慢指针迟早会重合,这可以作为判断是否有环的评判标准。
- 题目:获取单向链表的环的入口结点。
- 思路:当快慢指针相遇时,我们可以判断到链表中有环,这时重新设定一个新指针指向链表的起点,且步长与慢指针一样为1,则慢指针与“新”指针相遇的地方就是环的入口。证明这一结论牵涉到数论的知识,这里略,只讲实现。
- 代码实现:
package com.ex.link; public class CircleTest { public static void main(String[] args) { //创建结点 Node<String> first = new Node<String>("aa", null); Node<String> second = new Node<String>("bb", null); Node<String> third = new Node<String>("cc", null); Node<String> fourth = new Node<String>("dd", null); Node<String> fifth = new Node<String>("ee", null); Node<String> six = new Node<String>("ff", null); Node<String> seven = new Node<String>("gg", null); //完成结点之间的指向 first.next = second; second.next = third; third.next = fourth; fourth.next = fifth; fifth.next = six; six.next = seven; seven.next=second; //查找中间值:必须是在无环的情况,否则会死循环 // System.out.println("中间值为:"+getMid(first)); //判断是否有环 System.out.println("是否有环:"+isCircle(first)); System.out.println("环的入口:"+getEntrance(first)); } /** * 获取环的入口 * @param first 首结点 * @return 如果有环,返回环的入口结点,如果无环,返回null */ private static Node getEntrance(Node<String> first) { //定义快慢指针 Node<String> slow=first,fast=first,temp=null; //移动快慢指针,当快慢指针相遇说明有环,给新指针初始化,开始同时移动新慢指针,二者相遇的地方即是环的入口,如过快慢指针没有相遇,则说明无环,返回null while (fast!=null && fast.next!=null){ //移动快慢指针 slow=slow.next; fast=fast.next.next; //判断快慢指针有无相遇 if (slow==fast){ //有环,给新指针初始化 temp=first; //跳过此次循环,开启下次新慢指针的移动 break; } } if (fast!=slow){ return null; } while (slow!=temp){ slow=slow.next; temp=temp.next; } return slow; } /** * 判断是否有环 * @param first 首结点 */ private static boolean isCircle(Node<String> first) { //定义快慢指针 Node<String> slow=first,fast=first; //移动快慢指针,当快慢指针相遇(有环) 或 快指针指向尾结点(元素个数为偶数)/尾结点后的null(元素个数为奇数)(无环) 时结束 while (fast!=null && fast.next!=null){ //移动快慢指针 slow=slow.next; fast=fast.next.next; //判断是否相遇 if (slow==fast) { return true; } } return false; } /** * 获取中间值 * @param first 首结点 * @return 返回中间值 */ private static Node getMid(Node<String> first) { //定义快慢指针 Node<String> slow=first,fast=first; //移动快慢指针,当快指针指向尾结点(元素个数为偶数)或 尾结点后的null(元素个数为奇数) 时结束 while (fast!=null && fast.next!=null) {//注意条件和子条件的顺序 //移动快慢指针 slow=slow.next; fast=fast.next.next; } //返回慢指针对应节点的数据作为中间值 return slow; } private static class Node<T> { T item; Node next; public Node(T item, Node next) { this.item = item; this.next = next; } @Override public String toString() { return "Node{" + "item=" + item + '}'; } } }
3.约瑟夫问题
- 题目:
-
- 问题描述:传说有这样一个故事,在罗马人占领乔塔帕特后,39 个犹太人与约瑟夫及他的朋友躲到一个洞中,39个犹太人决
定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,第一个人从1开始报数,依次往
后,如果有人报数到3,那么这个人就必须自杀,然后再由他的下一个人重新从1开始报数,直到所有人都自杀身亡
为止。然而约瑟夫和他的朋友并不想遵从。于是,约瑟夫要他的朋友先假装遵从,他将朋友与自己安排在第16个与
第31个位置,从而逃过了这场死亡游戏 。
- 问题描述:传说有这样一个故事,在罗马人占领乔塔帕特后,39 个犹太人与约瑟夫及他的朋友躲到一个洞中,39个犹太人决
-
- 问题转换:41个人坐一圈,第一个人编号为1,第二个人编号为2,第n个人编号为n。
1.编号为1的人开始从1报数,依次向后,报数为3的那个人退出圈;
2.自退出那个人开始的下一个人再次从1开始报数,以此类推;
3.求出最后退出的那个人的编号。 - 图解:
- 问题转换:41个人坐一圈,第一个人编号为1,第二个人编号为2,第n个人编号为n。
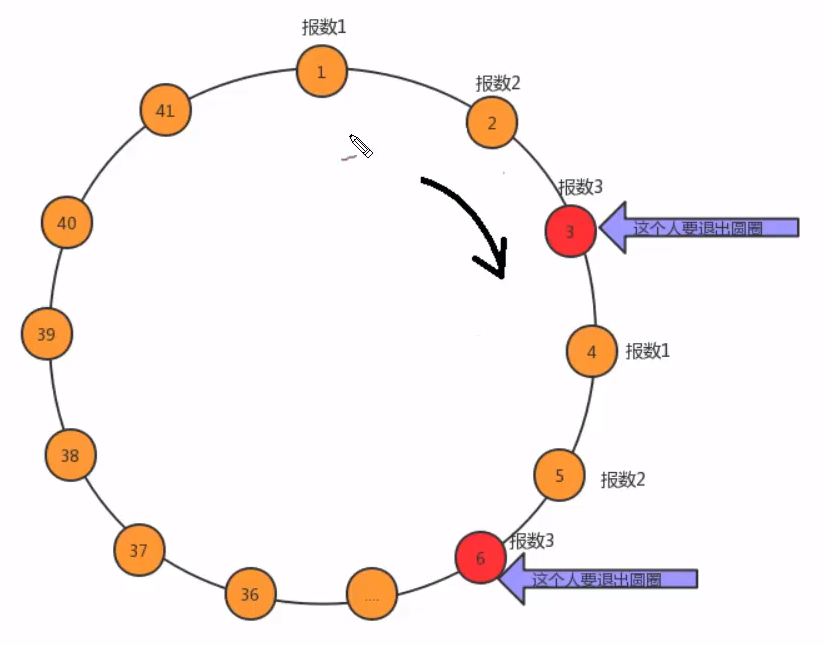
- 思路:用循环链表模拟这个圈。报数(计数器+1),如果是3,就让前面的人拿着匕首(前驱结点不做改变)鲨掉自己(前驱结点的指针指向后继结点)并擦匕首上的血(计数器归零),然后叫下一个人(指针后移)报数;如果不是3,就拿着匕首(前驱结点更新为当前结点),让下一个人报数。
- 实现代码:
package com.ex.link; /** * 实现约瑟夫问题 */ public class JosephProblem { public static void main(String[] args) { //1.构建循环链表 //first为首元素结点,curr记录当前链表的尾结点,以便于将下一个新结点加入链表 Node<Integer> first=new Node<>(1,null),curr=first; for (int i = 2; i <= 41; i++) { //加入新结点:创建结点并更新当前尾结点 Node<Integer> newNode = new Node(i,null); curr.next=newNode; curr=newNode; //最后一个结点:闭环 if (i==41){ newNode.next=first; } } //2.创建计数器 int count=0; //3.开始遍历 //n是当前这个人(当前结点),preNode是自杀用的匕首(前驱结点) Node n=first,preNode=null; while (n != n.next){//直到链表里只剩下一个元素结点,也就是只有一个人需要报数时结束(于是最后两个人一商量,都不自杀了) //报数 count++; //判断是否需要自杀 if (count==3){ //如果是3就准备自杀,并重置计数器为0,然后把匕首给下一个人 preNode.next=n.next; System.out.print(n.item+" "); count=0; n=n.next; }else { //如果不是3,就直接叫下一个人,并把匕首给下一个人,叫他报数 preNode=n; n=n.next; } } //输出最后剩下的那个人 System.out.print(n.item+" "); } private static class Node<T> { T item; Node next; public Node(T item, Node next) { this.item = item; this.next = next; } @Override public String toString() { return "Node{" + "item=" + item + '}'; } } }
四、链表的官方实现
以JDK1.8为参考:
链表类 LinkedList<T> 底层采用双向链表,非线程安全。
和上面自定义的双向链表一样,成员变量为首尾结点和元素数量,但不同的是,LinkedList类的首结点不是辅助结点,而是真正存数据,当链表为空时插入结点是将新结点作为了首结点,而不是首结点指向新结点。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号