利用FPGA控制永磁同步电机(一)—电磁关系

电磁CP的发现

1820年，奥斯特发表论文《关于磁针上电流碰撞的实验》，揭示了电流的磁效应。

论文起源于一个偶然的实验：在电池的两极间接上一根很细的铂丝，在铂丝下方放置一枚磁针，接通电源后磁针旋转到与铂丝相垂直的方向；改变电流方向后发现磁针又向相反的方向旋转。

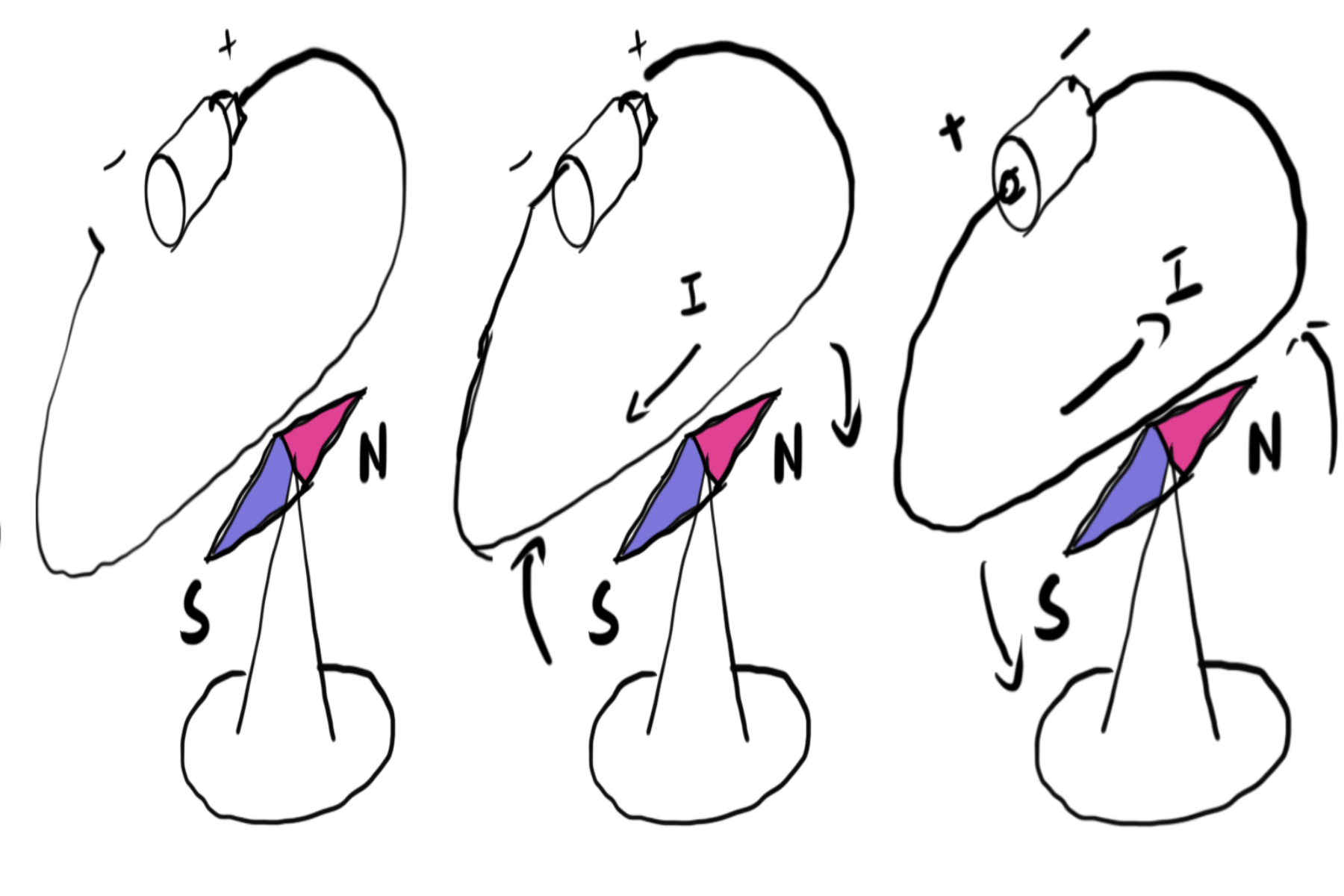
实验是偶然的，但成功并不是偶然的。奥斯特青年时代就是康德哲学的崇拜者，他1799年的博士论文讨论的就是康德哲学。基于其哲学倾向，奥斯特一直坚信电磁之间一定有某种关系。在1812年出版的《关于化学力和电力的统一的研究》一书中，奥斯特推测，既然电流通过较细的导线会发热，那么通过更细的导线就可能发光，导线直径再小下去就可能产生磁效应。沿着这个思路，奥斯特做了许多实验都没成功，直到发表论文前的这次偶然实验。

这篇论文只有四页，但却有着划时代的意义。1934年起，人们用“奥斯特”的名字来命名磁场强度。

电生磁

奥斯特发现电磁之间的存在某种联系后，大群的科学家投入到相关方向的研究。

安培也是其中之一。安培通过实验发现长直导线外，到导线距离相等的点“磁场”大小相等；距离不同的点“磁场”大小与距离成反比；“磁场”和电流大小以及导线的根数也成正比。假如用\(\overrightarrow{H}\)(现在的确是用\(\overrightarrow{H}\))来表示“磁场”的大小，则易知：

\(\overrightarrow{H} \propto \frac{N \vec{i}}{\vec{r}}\)

当用半径为\(r\)的圆时，其“磁场”大小为：

\(\overrightarrow{H} = \frac{N i}{2 \pi \vec{r}}\)

而后安培又将其拓展为任意的曲线：在恒定电流的磁场中，磁场强度\(\overrightarrow{H}\)沿任何闭合路径\(C\)(即环路积分)的线积分等于其所包围的电流强度的代数和，即

\(\oint_C \overrightarrow{H} \cdot \mathrm{d}r = Ni\)

这个公式暗含一个结论，那就是磁场是由运动的电荷(即电流)产生的。因此在电磁学中，把产生磁场的电流又叫做磁动势或磁势(Magnetomotive Force)，简写为MMF。

关于磁场强度的准确方向，在安培定律中已经用数学的方法给出，但一般情况下只需要知道磁场强度的大致方向，这种情况下有一种简单直观的方法，就是我们高中物理所学的安培定则。

安培定则，也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间关系的定则。通电直导线中的安培定则（安培定则一）：用右手握住通电直导线，让大拇指指向直导线中电流方向，那么四指指向就是通电导线周围磁场的方向；通电螺线管中的安培定则（安培定则二）：用右手握住通电螺线管，让四指指向电流的方向，那么大拇指所指的那一端是通电螺线管的N极。

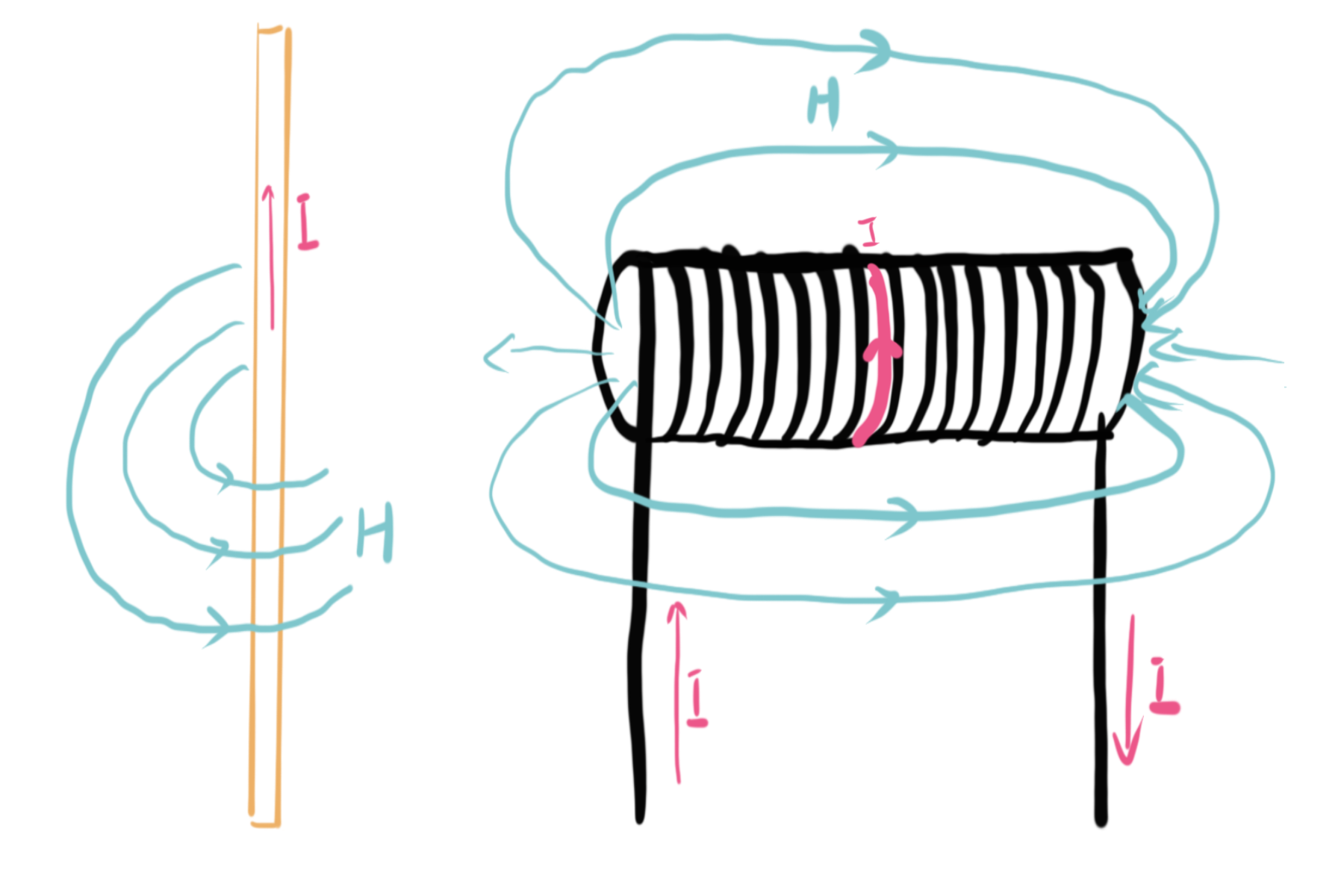
磁生电

法拉第于1831年的实验中发现电磁感应定律。

定性的描述：磁通量的变化产生感应电动势。

定量的描述：线圈中感应的电动势(Electromotive Force)，简称EMF，与每匝线圈中的磁通量的变化率以及匝数成正比，即

\(e = -N \frac{\mathrm{d}\varphi}{\mathrm{d}t}\)

那么问题就来了，什么是磁通量？其定义是

\(\varphi = \int_S \overrightarrow{B} \cdot \mathrm{d} \overrightarrow{S}\)

简单来说就是磁通密度乘以面积，那什么是磁通密度(又称磁感应强度)？

与电场强度\(\overrightarrow{E}\)是由单位点电荷受电场力的定义类似，磁通密度可以根据运动的点电荷在磁场中所受的磁场力来定义。

\(\overrightarrow{F} = q \overrightarrow{v} \times \overrightarrow{B}\)

这个公式是洛伦兹公式的简化版，即可以根据点电荷电量大小、运动速度以及所受的磁场力来反推周围磁场的大小。磁通密度的单位是特斯拉(Tesla)。

与磁场强度方向类似，感应电动势的方向在定律中也用数学的形式给出，但若仅想知道其大致方向，有一种更为简单直观的方法，楞次定律。

楞次定律：感应电流具有这样的方向，即感应电流的磁场总要阻碍引起感应电流的磁通量的变化。

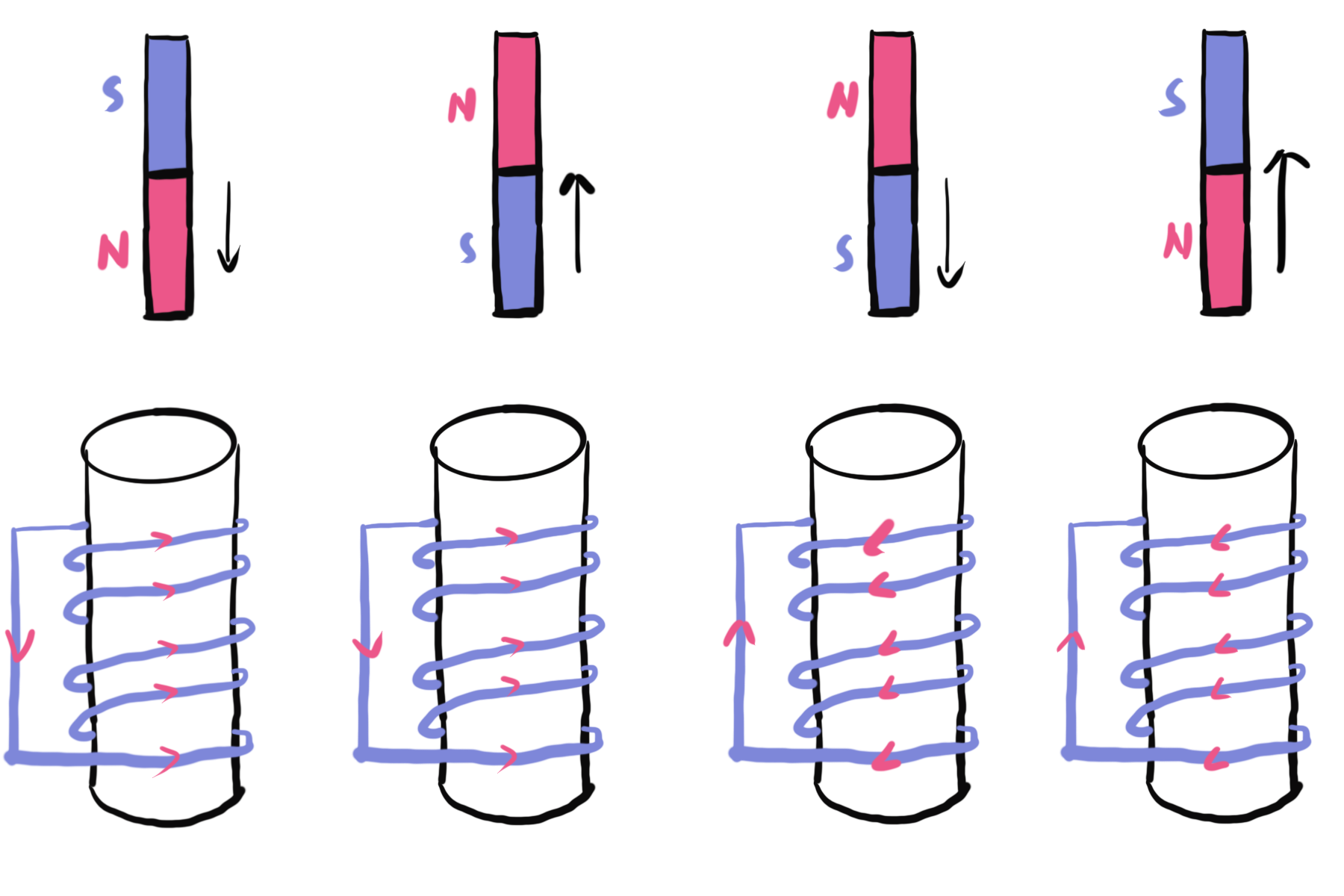
磁滞曲线

• 在安培环路定理中，说电流产生磁场，磁场的大小用\(\overrightarrow{H}\)来表示。
• 法拉第电磁感应中，又说可以通过受力来计算电荷感应到的磁场\(\overrightarrow{B}\)。

为什么用来表示磁场却有两个量？首先可以明确，\(\overrightarrow{H}\)和\(\overrightarrow{B}\)的量纲不同，两个量不能混为一谈。

把磁通密度\(\overrightarrow{B}\)与磁场强度\(\overrightarrow{H}\)之间的比值称为磁导率：

\(\overrightarrow{B} = \mu \overrightarrow{H}\)

磁导率\(\mu\)描述的是电荷感应的磁场(输出\(\overrightarrow{B}\))与电流产生的磁场(输入\(\overrightarrow{H}\))的比值，描述前者随后者的响应。既然是响应就会有幅度响应和相位响应，所以磁导率在本质上是一个复数。不过电机工作在低频段，完全可以忽略由磁导率带来的相位滞后，只需要分析其幅度响应。

为什么介质中磁场的输入和输出并不一致呢？因为有介质的影响。假设通过磁动势电流\(i\)把磁场\(\overrightarrow{H}\)加到某种材料中，材料中的带电粒子会受到磁场的影响改变运动方向，进而产生附加磁场，那么在该点处的总电场就不再是\(\overrightarrow{H}\)了。受外界磁场影响使得材料里也有额外磁场的过程称为“磁化”。

根据安培定律可知磁场是由电流产生的，因此材料的“磁化”也是因为其内部某种微观电流的改变引起的，这种微观电流可以简单的称之为分子电流(若具体分析材料“磁化”的机制需要考虑自由电流、分子电流及电子电流)。

简而言之，\(\overrightarrow{H}\)是外部的激发场，\(\overrightarrow{B}\)是总的响应场，在电机里面这两个量都非常重要，因为电机控制就是控制电压、电流以及力矩之间的关系，而：

• 电流和\(\overrightarrow{H}\)相关
• 力矩和\(\overrightarrow{B}\)相关

因此理解\(\overrightarrow{H}\)和\(\overrightarrow{B}\)的关系是学习电机的一个非常重要的知识点。

现假设用一个正弦的电流对介质进行磁化，电流的大小(代表\(\overrightarrow{H}\)的大小)如左，得到介质中的磁通密度\(\overrightarrow{B}\)为右。

可见\(\overrightarrow{H}\)和\(\overrightarrow{B}\)的并不是简单的线性关系，而是呈现一个滞环，一般称之为磁滞曲线。不同材料的磁滞曲线一般也不同。

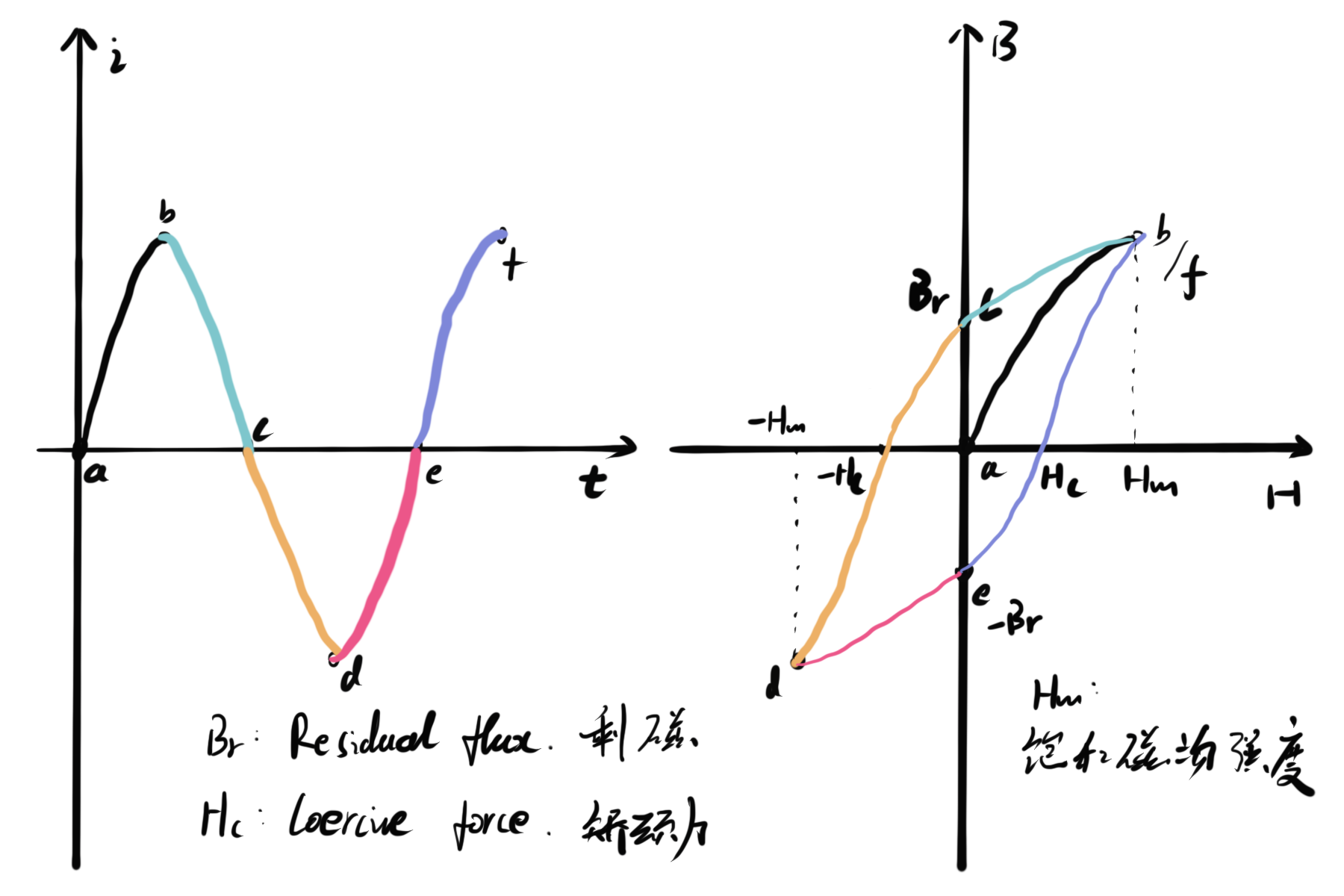
• 有的材料滞环较宽，也就是当励磁电流减为0后，磁通密度\(\overrightarrow{B}\)仍保持在一个较大的值。这种材料被称为硬磁材料或永磁体
• 有的材料滞环较窄，也就是当励磁电流减为0后，磁通密度\(\overrightarrow{B}\)也基本上减小到0。这种材料被称为软磁材料或导磁体

补充知识

由给定的电荷和电流产生场，称为电和磁激发(electric and magnetic excitation)，用\(\overrightarrow{D}\)和\(\overrightarrow{H}\)来描述。

在电磁场中的某一点，作用在速度为\(\overrightarrow{v}\)的点电荷\(q\)的力\(\overrightarrow{F}\)，定义了电场强度和磁通密度\(\overrightarrow{E}\)和\(\overrightarrow{B}\)。

\(\overrightarrow{E} = \frac{1}{\epsilon}\overrightarrow{D}\)

\(\overrightarrow{B}=\mu \overrightarrow{H}\)

\(\epsilon\)在分母而\(\mu\)在分子，这一事实源自于历史上理解电磁学本质所走的弯路。