并行课程Ⅲ

原题：leetcode 2050.并行课程Ⅲ

题目描述

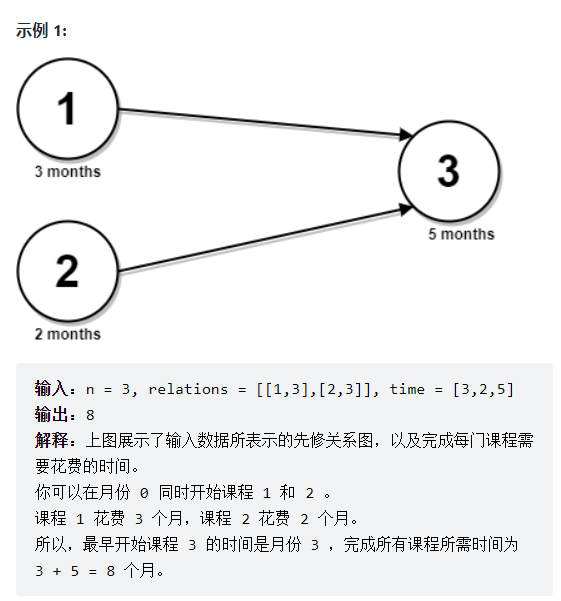
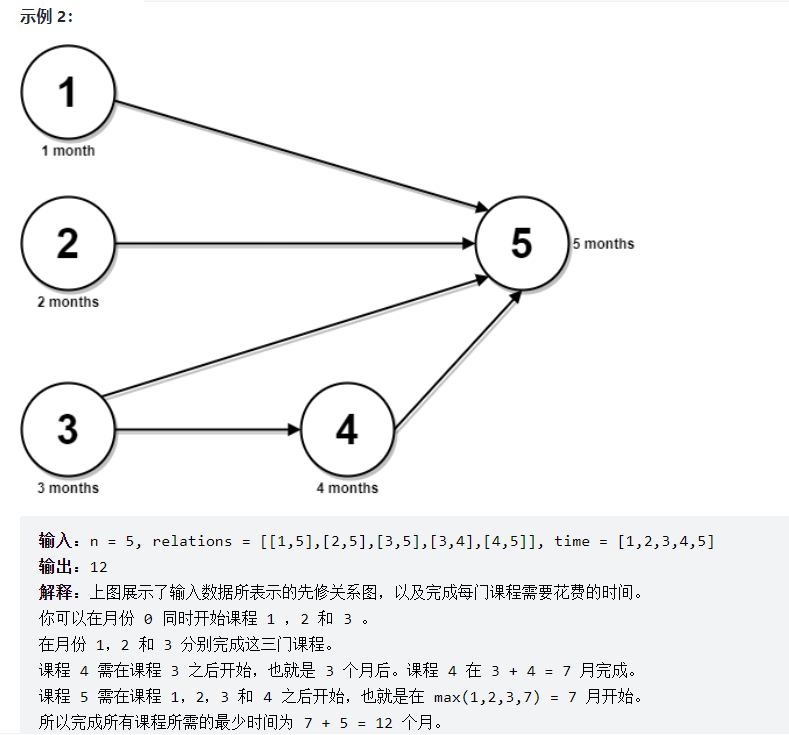
给你一个整数n，表示有n节课，课程编号从1到n。同时给你一个二维整数数组 relations ，其中 relations[j] = [prevCoursej, nextCoursej] ，表示课程 prevCoursej 必须在课程 nextCoursej 之前完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 time ，其中 time[i] 表示完成第 (i+1) 门课程需要花费的月份数。

请你根据以下规则算出完成所有课程所需要的最少月份数：

• 如果一门课的所有先修课都已经完成，你可以在 任意 时间开始这门课程。
  你可以同时上任意门课程。
• 请你返回完成所有课程所需要的最少月份数。

提示：

• 1 <= n <= 5 * 104
• 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
• relations[j].length == 2
• 1 <= prevCoursej, nextCoursej <= n
• prevCoursej != nextCoursej
• 所有的先修课程对 [prevCoursej, nextCoursej] 都是互不相同的。
• time.length == n
• 1 <= time[i] <= 104

题解

有向无环图，拓扑排序板子题，选取一个入度为0的顶点进入，在有向图中删去此顶点和所有以它结尾的边，直到图空为止。

const int maxn=50005;
class Solution {
public:
    int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
        vector<int>degree(maxn,0);
        vector<int>ans(maxn);
        for(int i=1;i<=n;i++) ans[i]=time[i-1];
        vector<int> v[maxn];
        for(int i=0;i<relations.size();i++){
            int from=relations[i][0];
            int to=relations[i][1];
            degree[to]++;
            v[from].push_back(to);
        }//建图
        queue<int>q;
        for(int i=1;i<=n;i++){
            if(degree[i]==0) q.push(i);
        }//初始化
        int ret=0;
        while(!q.empty()){//拓扑排序
            int now=q.front();
            q.pop();
            for(int i=0;i<v[now].size();i++){
                int next=v[now][i];
                degree[next]--;
                ans[next]=max(ans[next],ans[now]+time[next-1]);
                //ret=max(ret,ans[next]);
                if(!degree[next]) q.push(next);
            }
        }
        for(int i=1;i<=n;i++) ret=max(ret,ans[i]);
        return ret;
    }
};