OO第一单元总结
雄关漫道真如铁,而今迈步从头越。从头越,苍山如海,残阳如血。 ——毛润之
万事开头难,OO在所有专业课中又是一门较难的课程,只有抱着不断精进的决心,奋发突破,才能一口气到达终点。
程序结构分析
第一次作业
第一次作业需要完成的任务是简单多项式函数的求导。
类关系图:
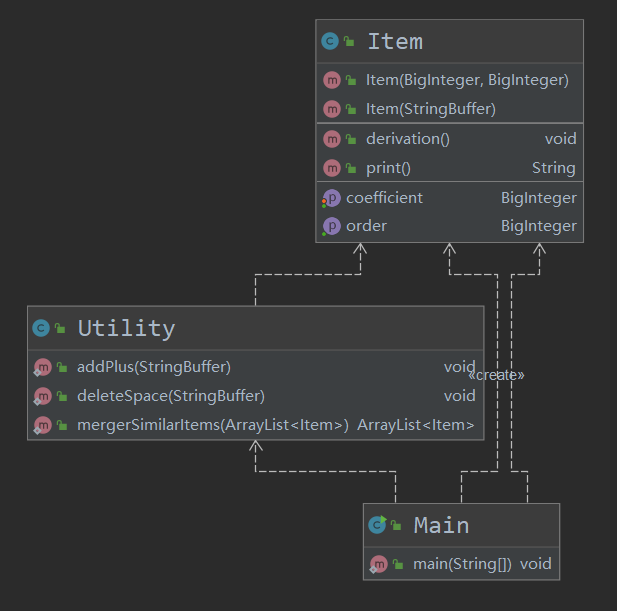
如图所示,第一次作业采用最朴素的思想构造三个类:Main类唯一方法主要负责读入、字符串预处理、对字符串操作方法的依次调入以及队最终结果的输出控制·;Utility类主要负责整个多项式的操作,有根据符号连接项、合并同类项操作;Item类负责存储每一个项的系数与指数,并拥有求导和打印方法。
度量分析:
ev, iv, v分别代指基本复杂度(Essential Complexity (ev(G))、模块设计复杂度(Module Design Complexity (iv(G)))、Cyclomatic Complexity (v(G))圈复杂度。
基本复杂度 是用来衡量程序非结构化程度的,非结构成分降低了程序的质量,增加了代码的维护难度,使程序难于理解。
基本复杂度高意味着非结构化程度高,难以模块化和维护,消除了一个错误有时会引起其他的错误。
模块设计复杂度 用来衡量模块判定结构,即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高,这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度,因此模块设计复杂度通常远小于圈复杂度。
圈复杂度 是用来衡量一个模块判定结构的复杂程度,数量上表现为独立路径的条数,即合理的预防错误所需测试的最少路径条数,圈复杂度大说明程序代码可能质量低且难于测试和维护,经验表明,程序的可能错误和高的圈复杂度有着很大关系。
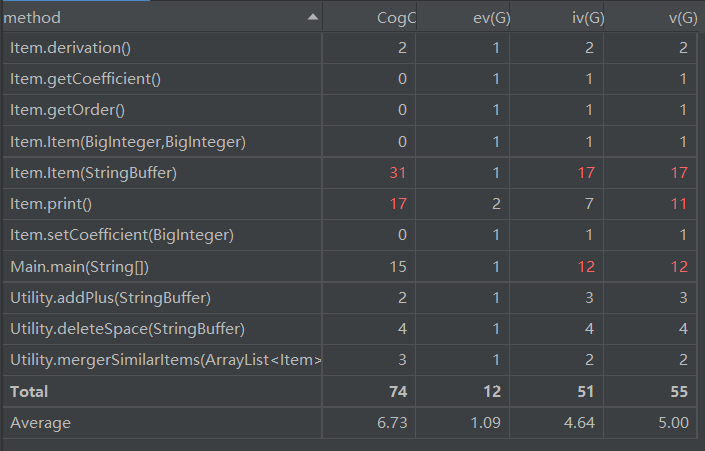
第一次作业逻辑比较简单,只有Item类的以StringBuffer为参数的构造器方法有较高的模块设计复杂度,其余方法复杂度基本都在合理范围之内。
第二次作业在上次作业的基础上增加了简单正余弦函数的求导。
类关系图:
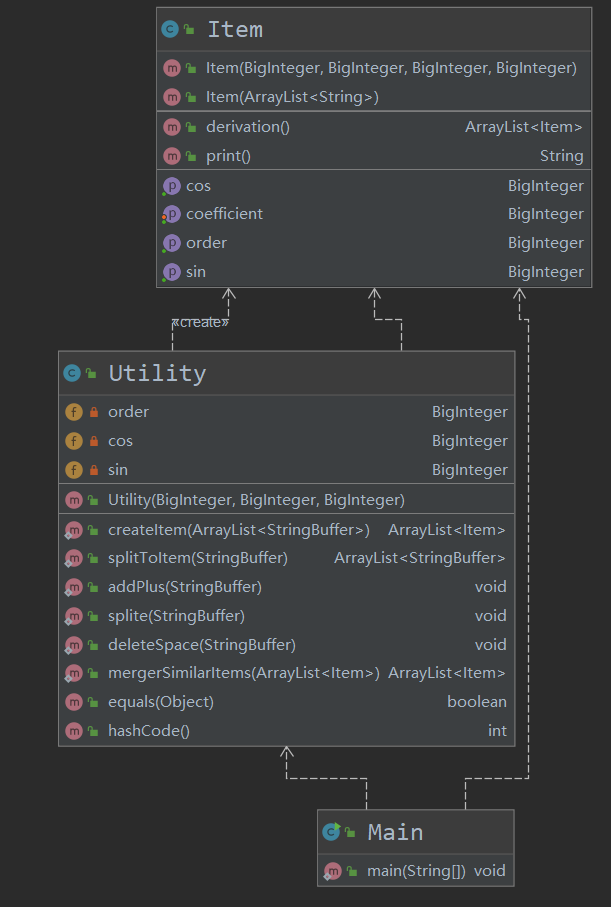
第二次作业基本沿用了第一次作业的架构, 在其基础上对Item类增加了cos、sin的记录,并对多项式类增加了以括号为界切分、切分到项的方法,并重载了hashCode方法以满足对相同hash键值的同类项合并的要求。
度量分析:
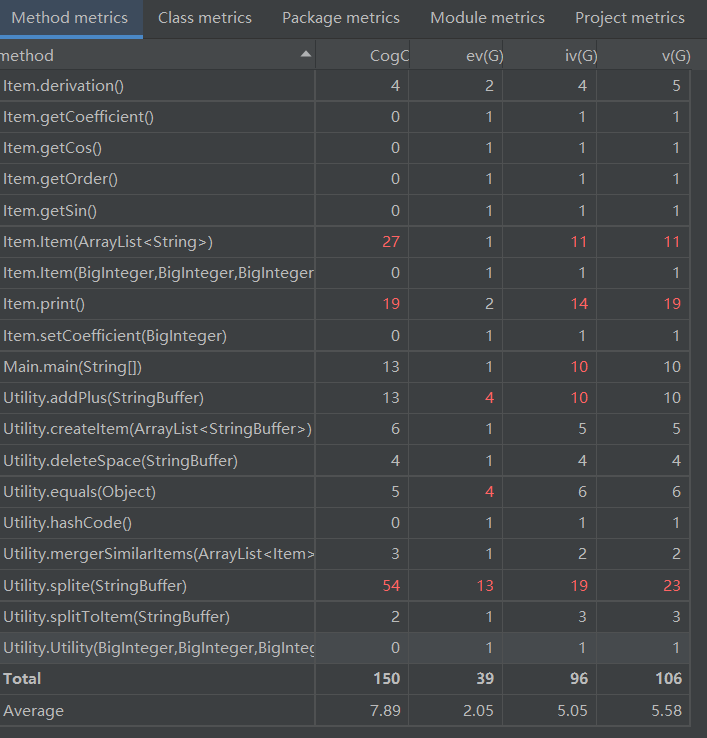
多项式类中的splite方法由于涉及带括号的切分,在方法内部嵌套调用了自己,因此导致其复杂度较高。
第三次作业在上次作业的基础上增加了嵌套组合函数形式的求导。
类关系图:
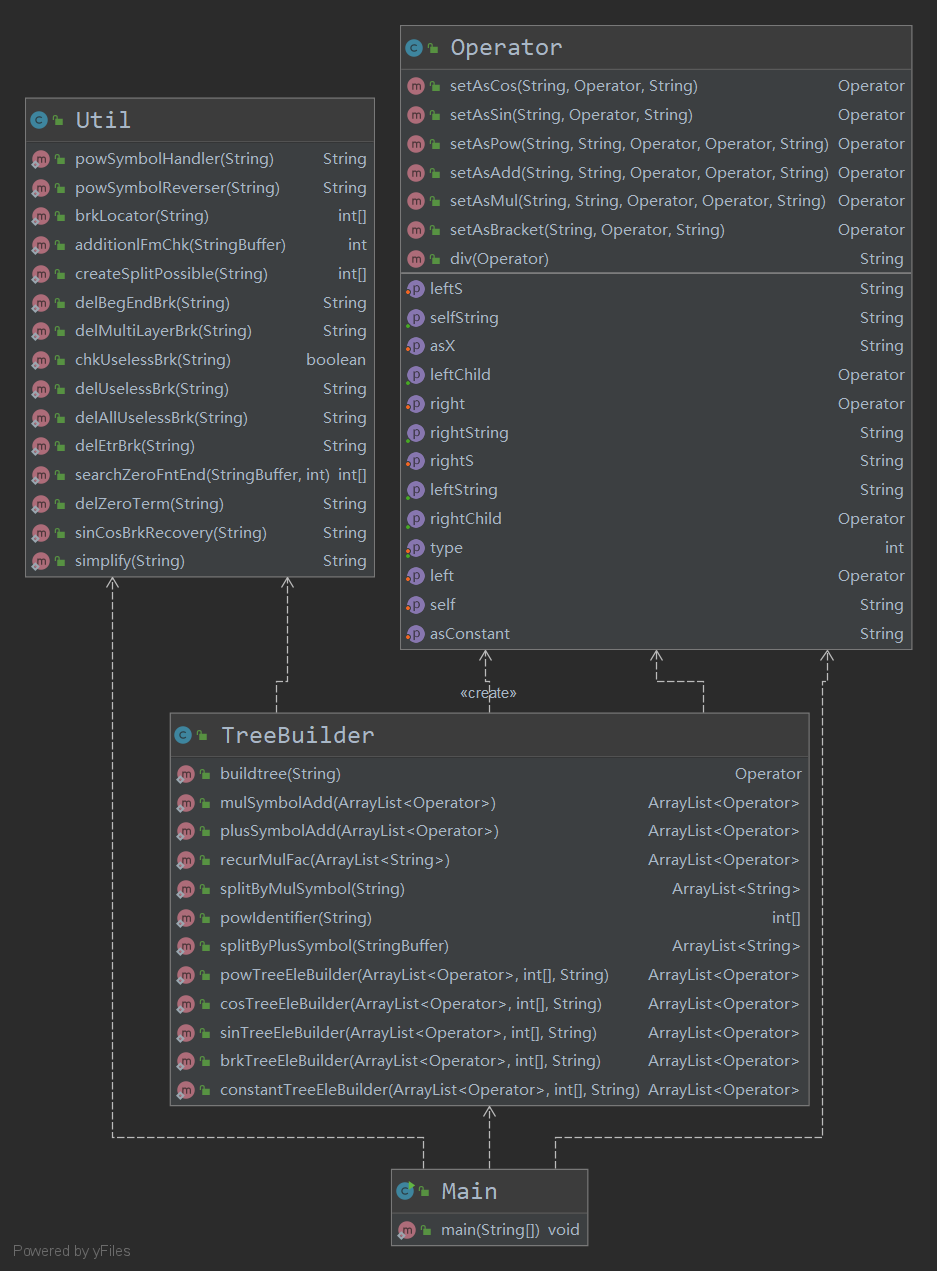
如图所示,第三次作业主要根据作业提示,将输入表达式构建成了一个表达式树。Util类主要负责多项式的预处理、分解与化简,TreeBuilder类主要负责识别项与构建整个表达式树,Operator类作为树节点负责保存自己、左子、右子节点的Operator类对象以供TreeBuilder类使用。
Bug修复与重构
在测试、互测过程中,一共在第二次作业中发现一处bug,原因是在处理+++1格式时把处理放在了空格处理方法之前,调换方法位置,问题即得到修复。
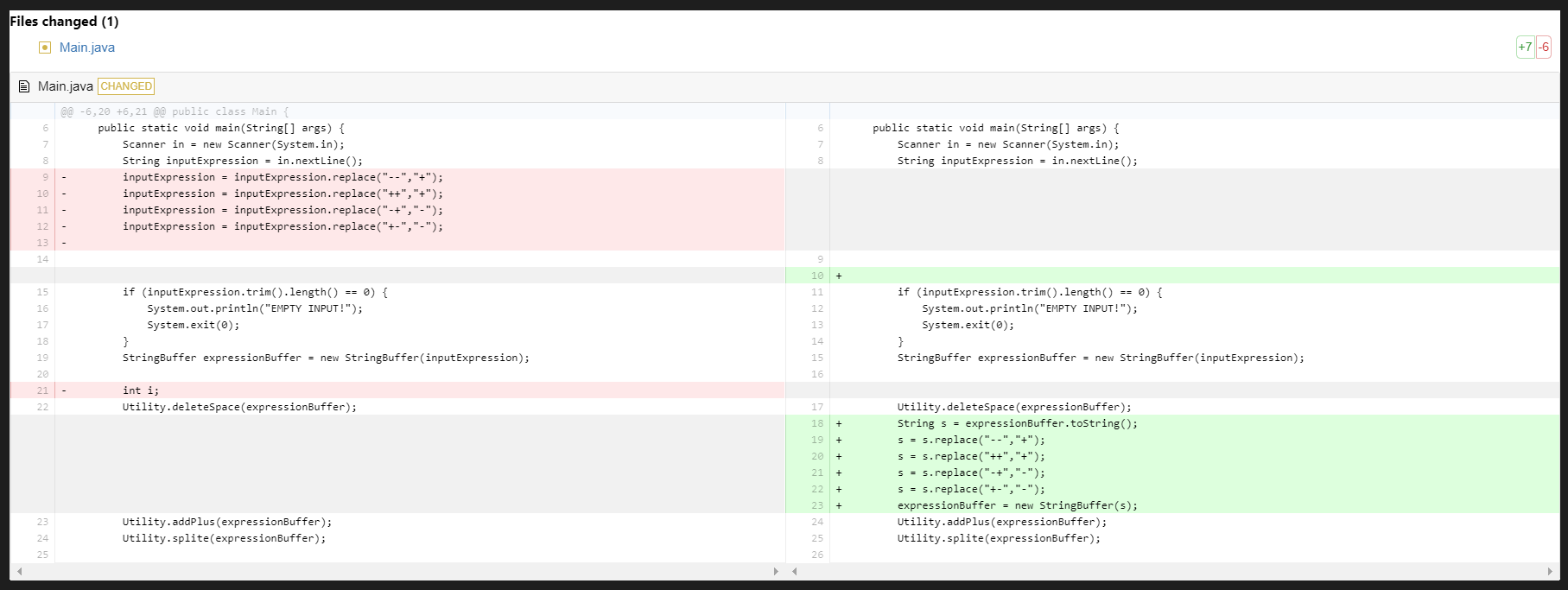
第一二次作业因为逻辑不复杂,使用简单结构就解决了问题,第三次作业利用指导书提示,将输入表达式首先生成一个表达式树结构,逐层求导,结构较前两次更加清晰。
hack方法
在互测过程中,我主要采用黑盒测试方法,首先是测试一些自己写完后曾经出现过问题的简单样例,例如+++1、---x、空格与符号交错等格式的项之间的组合,这些测试点的优点是构造简单,首先能够排除某位成员不具有哪些类型的bug。
之后再采用自动评测,利用随机数生成1000个合法表达式,再利用java输出与sympy得到的求导结果相比较确认目标是否存在bug。
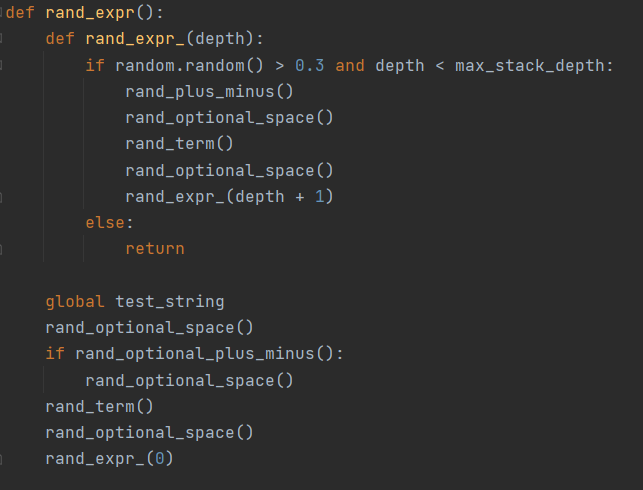

自动评测的优点是大量、无遗漏,但缺点是利用本方法生成的输入表达式往往过于冗杂,不能直接作为hack的标准输入提交,在hack成功后还需要人眼甄别bug项或组合。
心得体会
完成第一单元作业后,主要的收获有以下几点。
1.OOP的思想:
属性+方法=类
物以类聚,分类的思维模式要求我们:思考问题首先思考解决问题需要哪些分类,然后对这些分类单独思考,最后才对某个分类下的细节进行面向过程的思考。
本质:以类的方式组织代码,以对象的形式封装数据!
2.java一些常用工具的使用方法:
例如正则表达式、ArrayList变长数组、StringBuffer变长字符串、AtomicReference原子操作等。
总的来说,第一单元递进的三次作业很好地开启了OOP的大门。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号