DS博客作业06--图
1.本周学习总结
1.1思维导图
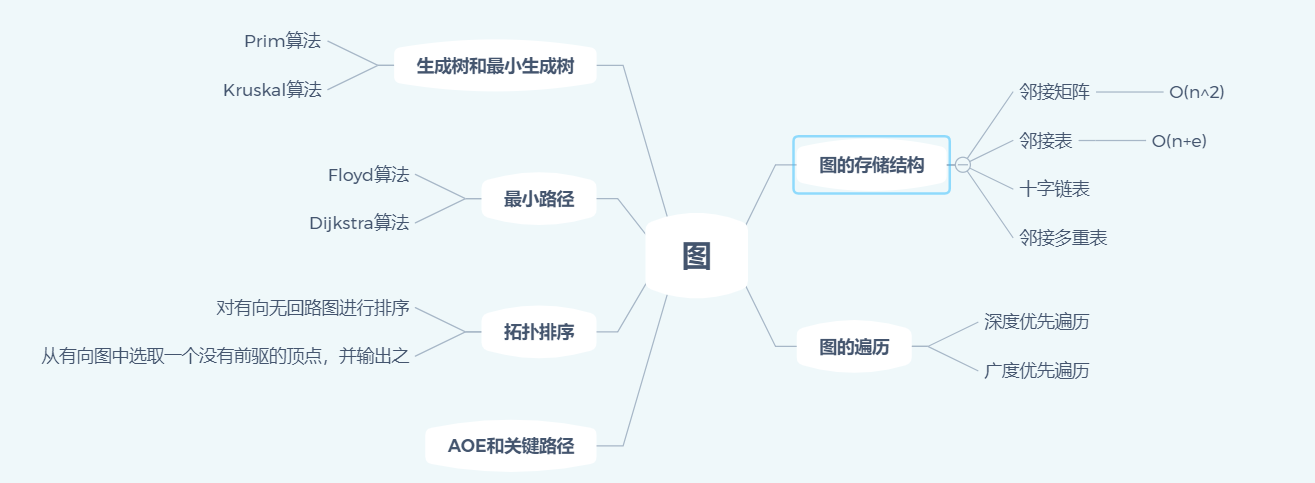
1.2体会
图的存储结构相对于线性表和树来说更为复杂,更加灵活。在解决有关图的问题上,比起自己摸索,还是掌握已有的高效算法来的实际。什么题目适合哪种图存储结构,用哪种算法比较简单,这都是在做题前要认真思考的。很多时候,没有用好方法容易让简单的问题复杂化。而在后续的学习中,我们利用STL的基础设施,就可以很快的搭建Graph。
2.PTA实验作业
2.1题目一:六度空间
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”
2.1.1设计思路
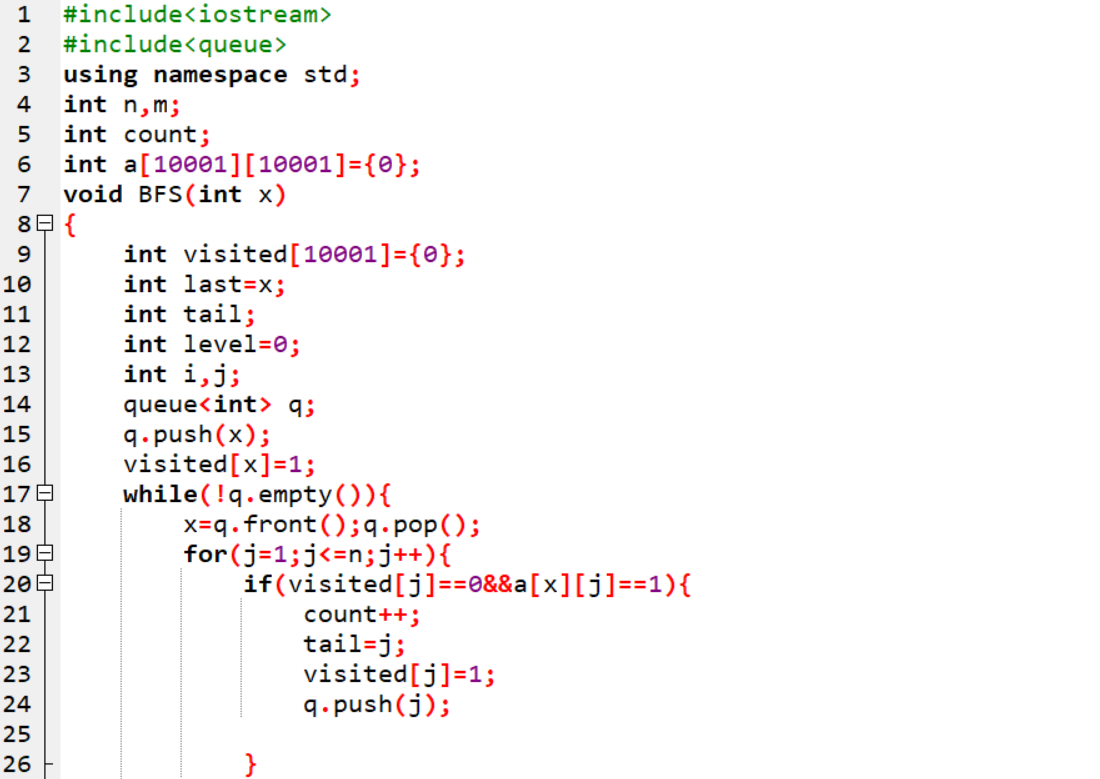
BFS函数
{
定义数组visited并初始化为0;
定义last=x,level=0,tail;
定义i,j;
定义整型队列q;
将x入队;
visited[x]=1;
while 队不为空
x等于队头;出队;
for j=1 to j=n
if visited[j]等于0 且a[x][j]==1
count++;
tail等于j;
visited[j]等于1;
将j入队;
if x等于last
last++;
last等于tail;
if level等于6
结束循环;
}
main函数
{
定义a,b;
定义i;
输入n,m;
for i=1 to m
输入a,b;
a[b][c]=1;
a[c][b]=1;
for i=1 to n
count=1;
BFS(i);
输出i;
输出count;
return 0;
}
2.1.2代码截图


2.1.3本题PTA提交列表说明

- Q1:原本用到邻接矩阵做这道题,想的太复杂了,导致写出来很乱。
- A1:用一个全局变量a的二维数组,再用BFS遍历,过程就简单多了。
2.2题目二:图着色问题
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
2.2.1设计思路
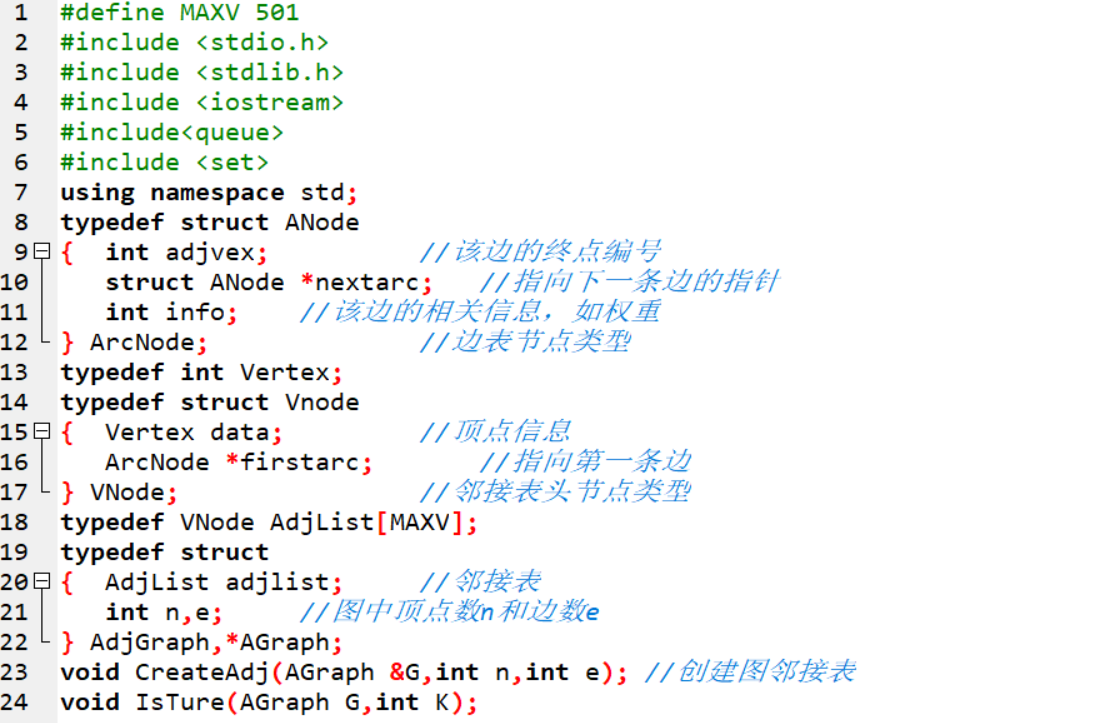
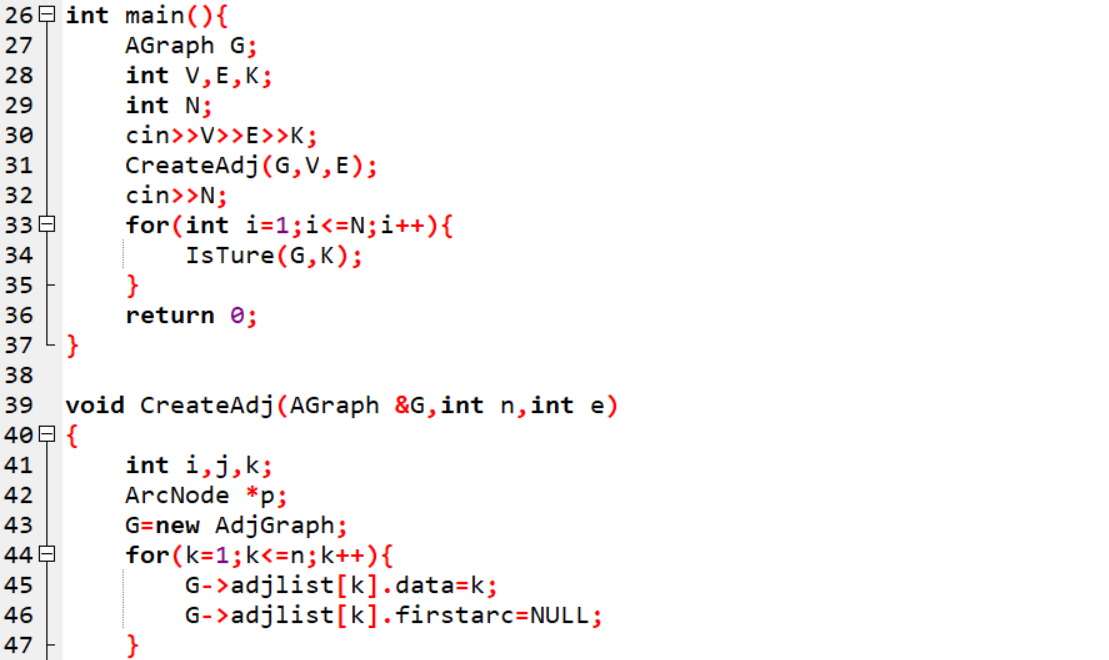
main函数
{
定义邻接表G;
int V,E,K;
int N;
输入 V,E,K;
创建邻接表CreateAdj(G,V,E);
输入N;
for i=1 to N
IsTrue(G,K)
return 0;
}
IsTrue函数
{
定义邻接表结点p;
定义set<int> s;
定义i,flag=0;
定义整型数组a并初始化0;
for i=1 to G->n
输入a[i];
s.insert(a[i]);
if s.size()!=k //若颜色数量不对
flag=1;
else
for i=1 to G->n
p=G->adjlist[i].firstarc;
while p不为NULL
if a[p->adjvex]等于a[i]
flag=1;
结束循环;
p=p->nextarc;
if flag等于0
输出“yes”;
else
输出“no”;
}
2.2.2代码截图
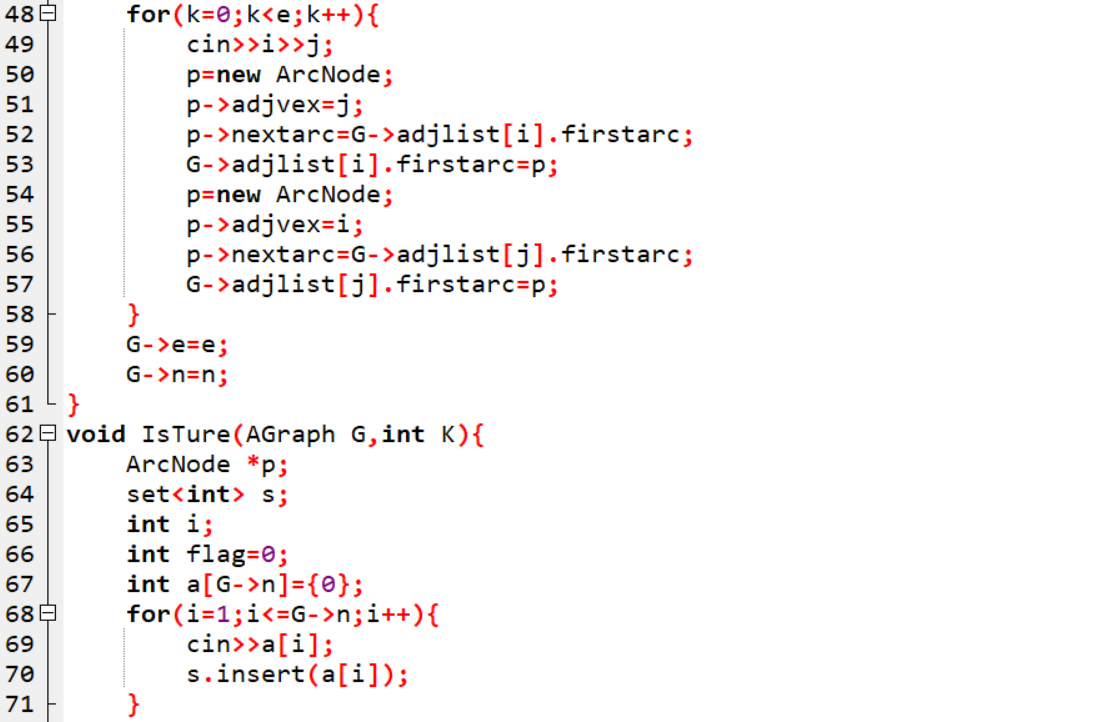

2.2.3本题PTA提交列表说明

- Q1:多种错误
- A1:刚开始写的时候想用数字来记录颜色数,后来发现不大可行,百度了其他代码,学着他们用了set,方便了许多。
- Q2:最大图时运行错误
- A2:把MAXV由500改为501就对了
2.3题目三:公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
2.3.1设计思路
findmin函数
{
定义minn=4556,index=1;
定义i;
for i=1 to N
if dist[i]不等于0且minn大于dist[i]
minn等于dist[i];
index等于i;
return index;
}
Prim函数
{
int cnt=1,cost=0;
int v;
for i=1 to N
parent[i]等于s;
dist[i] 等于c[i];
parent[s]等于-1;
dist[s]等于0;
while
v=findmin();
if(v==-1)结束循环;
cost+=dist[v];
cnt++;
dist[v]=0;
for i=1 to N
if dist[i]不等于0且c[v][i]小于dist[i]
dist[i]等于c[v][i];
parent[i]等于v;
if(cnt等于N)输出cost;
else 输出-1;
}
2.3.2代码截图
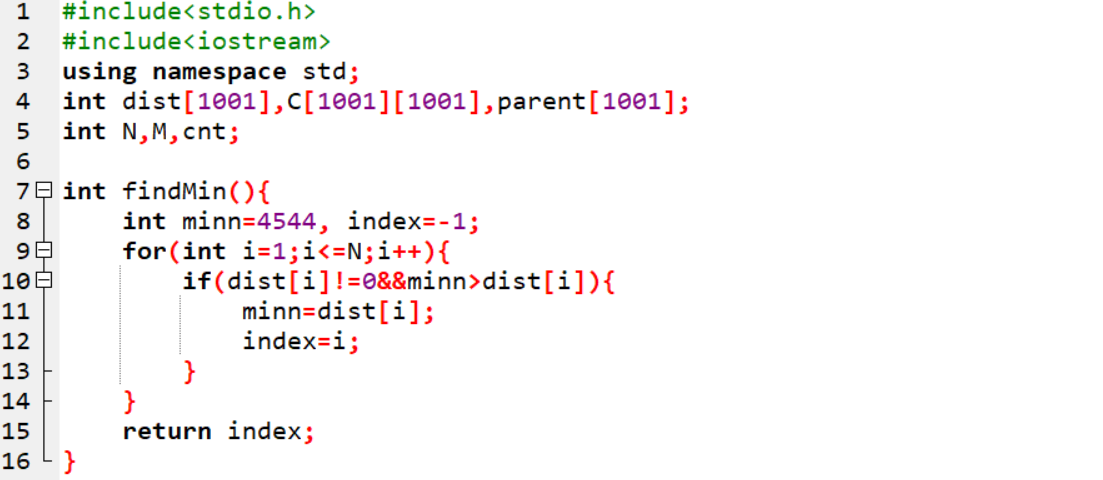

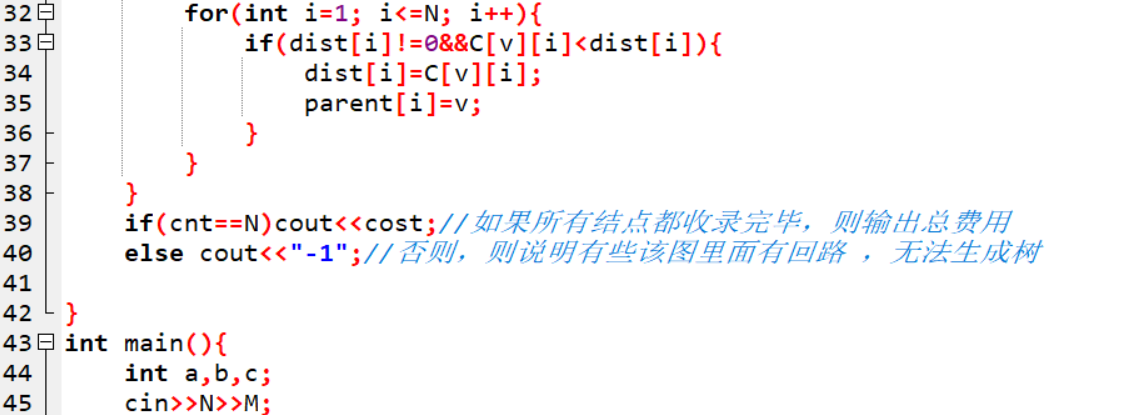
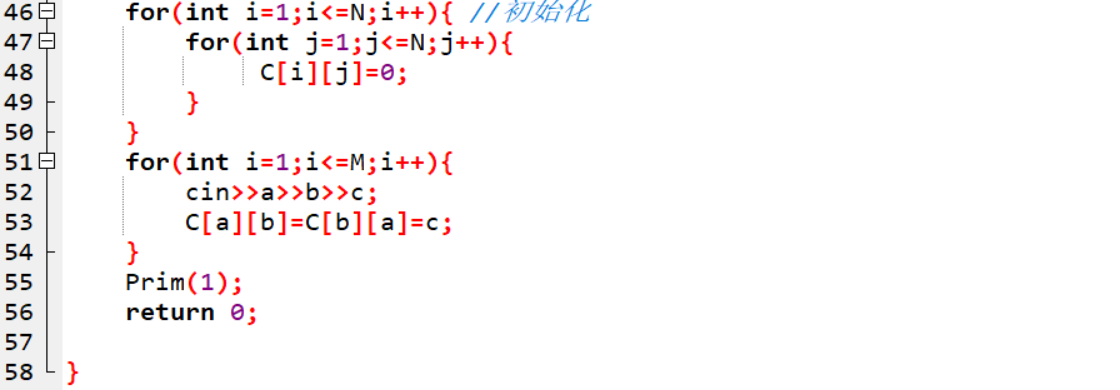
2.3.3本题PTA提交列表说明

3.上机考试错题及处理办法
题目:拓扑排序
给定一个有向图,求其拓扑序列,若有环路,输出error!
3.1截图错题代码
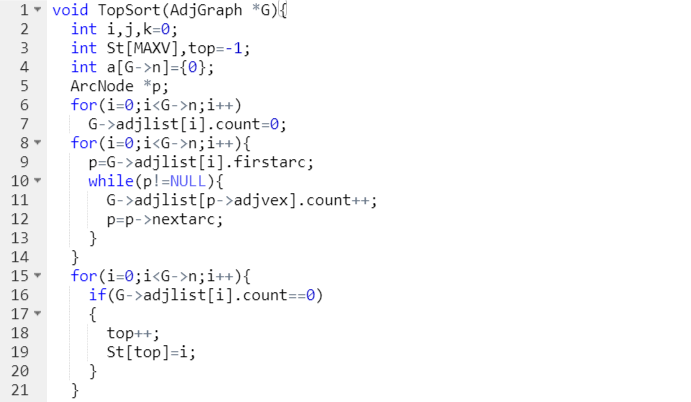
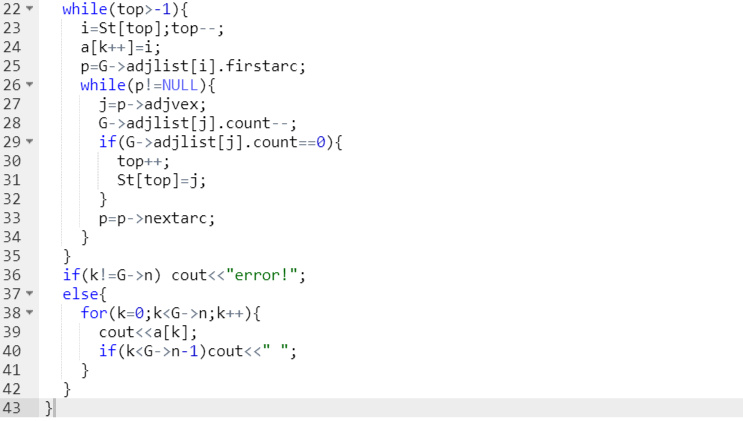
3.2错的原因及处理方法到
- 1.刚开始测试点1出现了答案错误,检查后发现是在输出函数时的循环条件写错了,记录结点数的k应该从0开始到G->n才对。
- 2.在提交时,忘记把测试时的*改回空格,导致答案错误。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号