图论
目录
\(DFS\)
\(DFS\) 全称是 \(Depth\ First\ Search\),中文名是深度优先搜索,是一种用于遍历或搜索树或图的算法。所谓深度优先,就是说每次都尝试向更深的节点走。
\(DFS\) 最显著的特征在于其 递归调用自身。同时与 \(BFS\) 类似,\(DFS\) 会对其访问过的点打上访问标记,在遍历图时跳过已打过标记的点,以确保 每个点仅访问一次。符合以上两条规则的函数,便是广义上的 \(DFS\)。
该算法通常的时间复杂度为 \(O(n+m)\),空间复杂度为 \(O(n)\),其中 \(n\) 表示点数,\(m\) 表示边数。注意空间复杂度包含了栈空间,栈空间的空间复杂度是 \(O(n)\) 的。在平均 \(O(1)\) 遍历一条边的条件下才能达到此时间复杂度,例如用前向星或邻接表存储图;如果用邻接矩阵则不一定能达到此复杂度。
数组邻接表
void dfs(int u)
{
st[u] = 1;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!st[j])
{
dfs(j);
}
}
}
vector邻接表
void dfs(int u)
{
st[u] = 1;
for(int i = 0; i < e[u].size(); i ++)
{
int v = e[u][i], ww = w[u][i];
if(!st[u])
{
dfs(v);
}
}
}
\(DFS\)序列
\(DFS\) 序列是指 \(DFS\) 调用过程中访问的节点编号的序列。
每个子树都对应 \(DFS\) 序列中的连续一段(一段区间)。
括号序列
\(DFS\) 进入某个节点的时候记录一个左括号 (,退出某个节点的时候记录一个右括号 )。
每个节点会出现两次。相邻两个节点的深度相差 \(1\)。
一般图上 \(DFS\)
对于非连通图,只能访问到起点所在的连通分量。
对于连通图,\(DFS\) 序列通常不唯一。
注:树的 \(DFS\) 序列也是不唯一的。
在 \(DFS\) 过程中,通过记录每个节点从哪个点访问而来,可以建立一个树结构,称为 \(DFS\) 树。\(DFS\) 树是原图的一个生成树。
例1. 全排列
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
int s[100];
bool p[100];
void dfs(int u, int fa)
{
if(u > fa)
{
for(int i = 1; i <= fa; i ++)
cout << s[i] << ' ';
cout << '\n';
}
for(int i = 1; i <= fa; i ++)
{
if(!p[i])
{
s[u] = i;
p[i] = true;
dfs(u + 1, fa);
p[i] = false;
s[u] = 0;
}
}
}
void solve()
{
int n;
cin >> n;
for(int i = 0; i <= n; i ++)
s[i] = p[i] = 0;
dfs(1, n);
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return 0;
}
例2. 八皇后
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
int ans, a[100], b[100], n, m;
bool check(int x, int y)
{
for(int i = 1; i <= x; i ++)
{
if(a[i] == y||i + a[i] == x + y||i - a[i] == x - y)
return false;
}
return true;
}
void dfs(int r)
{
if(r == n + 1)
{
ans ++;
return ;
}
for(int i = 1; i <= n; i ++)
if(check(r, i))
{
a[r] = i;
dfs(r + 1);
a[r] = 0;
}
}
void init()
{
for(n = 1; n <= 10; n ++)
{
ans = 0;
dfs(1);
b[n] = ans;
}
}
void solve()
{
while(cin >> m, m)
cout << b[m] << '\n';
}
signed main()
{
IOS; init();
int _ = 1;
// cin >> _;
while(_ --)
solve();
return 0;
}
\(BFS\)
\(BFS\) 全称是 \(Breadth\ First\ Search\),中文名是宽度优先搜索,也叫广度优先搜索。
是图上最基础、最重要的搜索算法之一。
所谓宽度优先。就是每次都尝试访问同一层的节点。 如果同一层都访问完了,再访问下一层。
这样做的结果是,\(BFS\) 算法找到的路径是从起点开始的 最短 合法路径。换言之,这条路径所包含的边数最小。
在 \(BFS\) 结束时,每个节点都是通过从起点到该点的最短路径访问的。
时间复杂度: \(O(n + m)\)
空间复杂度: \(O(n)\)(\(vis\) 数组和队列)
数组邻接表
void bfs(int u)
{
int hh = 0, tt = -1;
q[++ tt] = u;
st[u] = true;
while(hh <= tt)
{
int t = q[hh ++];
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(!st[j])
{
st[j] = true;
q[++ tt] = j;
}
}
}
}
vector邻接表
void bfs(int u)
{
queue<int> q;
q.push(u);
st[u] = true;
while(!q.empty())
{
int t = q.front();
q.pop();
for(int i = 0; i < e[t].size(); i ++)
{
int j = e[t][i];
if(!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
树上问题
树的直径
树上任意两节点之间最长的简单路径即为树的「直径」。
最近公共祖先LCA
最近公共祖先简称 \(LCA(Lowest Common Ancestor)\)。两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。 为了方便,我们记某点集 \(S=\{v_1,v_2,\ldots,v_n\}\) 的最近公共祖先为 \(\text{LCA}(v_1,v_2,\ldots,v_n)\) 或 \(\text{LCA}(S)\)
例. 距离
题目描述:
给出 \(n\) 个点的一棵树,多次询问两点之间的最短距离。
注意:边是无向的。所有节点的编号是 \(1,2,…,n\)。
输入格式:
第一行为两个整数 \(n\) 和 \(m\) 。\(n\) 表示点数,\(m\) 表示询问次数;
下来 \(n−1\) 行,每行三个整数 \(x,y,k\),表示点 \(x\) 和点 \(y\) 之间存在一条边长度为 \(k\);
再接下来 \(m\) 行,每行两个整数 \(x,y\),表示询问点 \(x\) 到点 \(y\) 的最短距离。
树中结点编号从 \(1\) 到 \(n\)。
输出格式:
共 \(m\) 行,对于每次询问,输出一行询问结果。
输入1
2 2
1 2 100
1 2
2 1
输出1
100
100
输入2
3 2
1 2 10
3 1 15
1 2
3 2
输出2
10
25
数据范围
\(2≤n≤10^4,1≤m≤2×10^4,0<k≤100,1≤x,y≤n\)
LCA模板
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 1e5 + 10, M = N * 2, S = 16;
int h[N], w[M], e[M], ne[M], idx;
int fa[N][S], ce[N];
int q[N], dist[N];
int n, m, root;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
void LCA_init()
{
int hh = 0, tt = -1;
ce[root] = 1;
q[++ tt] = root;
while(hh <= tt)
{
int t = q[hh ++];
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(ce[j] == 0)
{
ce[j] = ce[t] + 1;
dist[j] = dist[t] + w[i];
q[++ tt] = j;
fa[j][0] = t;
for(int k = 1; k < 15; k ++)
fa[j][k] = fa[fa[j][k - 1]][k - 1];
}
}
}
}
int query(int a, int b)
{
if(ce[a] < ce[b]) swap(a, b);
for(int i = 14; i >= 0; i --)
if(ce[fa[a][i]] >= ce[b])
a = fa[a][i];
if(a == b) return a;
for(int i = 14; i >= 0; i --)
if(fa[a][i] != fa[b][i])
{
a = fa[a][i];
b = fa[b][i];
}
return fa[a][0];
}
void solve()
{
memset(h, -1, sizeof h);
root = 1;
cin >> n >> m;
int a, b, c;
for(int i = 1; i < n; i ++)
{
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
LCA_init();
int x, y, ans;
while(m --)
{
cin >> x >> y;
ans = dist[x] + dist[y] - 2 * dist[query(x, y)];
cout << ans << "\n";
}
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
树链剖分
树的层次
题目描述:
给定一个 \(n\) 个点 \(m\) 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 \(1\),点的编号为 \(1∼n\)。
请你求出 \(1\) 号点到 \(n\) 号点的最短距离,如果从 \(1\) 号点无法走到 \(n\) 号点,输出 \(−1\)。
输入格式:
第一行包含两个整数 \(n\) 和 \(m\) 。
接下来 \(m\) 行,每行包含两个整数 \(a\) 和 \(b\),表示存在一条从 \(a\) 走到 \(b\) 的长度为 \(1\) 的边。
输出格式:
输出一个整数,表示 \(1\) 号点到 \(n\) 号点的最短距离。
输入
4 5
1 2
2 3
3 4
1 3
1 4
输出
1
数据范围
\(1≤n,m≤10^5\)
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int q[N], d[N], n, m;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int bfs()
{
memset(d, -1, sizeof(d));
int tt = 0, hh = 0;
q[0] = 1, d[1] = 0;
while(hh <= tt)
{
int t = q[hh ++];
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(d[j] == -1)
{
d[j] = d[t] + 1;
q[++ tt] = j;
}
}
}
return d[n];
}
void solve()
{
memset(h, -1, sizeof(h));
cin >> n >> m;
for(int i = 0; i < m; i ++)
{
int a, b;
cin >> a >> b;
add(a, b);
}
cout << bfs() << endl;
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return 0;
}
树的重心
例. 树的重心
题目描述
给定一颗树,树中包含 \(n\) 个结点(编号 \(1∼n\))和 \(n−1\) 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式:
第一行包含整数 \(n\),表示树的结点数。
接下来 \(n−1\) 行,每行包含两个整数 \(a\) 和 \(b\),表示点 \(a\) 和点 \(b\) 之间存在一条边。
输出格式:
输出一个整数 \(m\),表示将重心删除后,剩余各个连通块中点数的最大值。
输入
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出
4
数据范围
$1≤n≤10^5$11
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int h[N], e[M], ne[M], idx;
int n, ans = N;
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u)
{
st[u] = true;
int res = 0, sum = 1;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!st[j])
{
int s = dfs(j);
res = max(res, s);
sum += s;
}
}
res = max(res, n - sum);
ans = min(res, ans);
return sum;
}
void solve()
{
memset(h, -1, sizeof(h));
cin >> n;
for(int i = 0; i < n - 1; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
dfs(1);
cout << ans << endl;
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return 0;
}
最短路
多源汇\(Floyd\)
时间复杂度:\(O(n^3)\)
Floyd
void floyd()
{
for(int k = 1; k <= n; k ++)
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
p[i][j] = min(p[i][j], p[i][k] + p[k][j]);
}
单源朴素\(Dijkstra\)
时间复杂度:\(O(nm)\)
朴素Dijkstra
void Dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
for(int i = 0; i < n; i ++)
{
int t = -1;
for(int j = 1; j <= n; j ++)
if(!st[j]&&(t == -1||dist[j] < dist[t]))
t = j;
st[t] = 1;
for(int j = h[t]; j != -1; j = ne[j])
{
int i = e[j];
dist[i] = min(dist[i], dist[t] + w[j]);
}
}
}
单源堆优化\(Dijkstra\)
时间复杂度:\(O(mlog(n))\)
堆优化Dijkstra
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
priority_queue<pii, vector<pii>, greater<pii> > heap;
dist[1] = 0;
heap.push({0, 1});
while(heap.size())
{
auto t = heap.top();
heap.pop();
int y = t.second;
if(st[y]) continue;
st[y] = true;
for(int i = h[y]; ~i; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[y] + w[i])
{
dist[j] = dist[y] + w[i];
heap.push({dist[j], j});
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
单源\(Spfa\)
时间复杂度:\(O(nm)\)
Spfa
int spfa()
{
memset(dist, 0x3f, sizeof(dist));
queue<int> q;
dist[1] = 0; st[1] = true;
q.push(1);
while(q.size())
{
int t = q.front(); q.pop();
st[t] = false;
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if(!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
return dist[n];
}
最小生成树
\(Prim\)
时间复杂度:\(O(nm)\)
Prim
const int N = 510, inf = 0x3f3f3f3f;
int n, m, dist[N], g[N][N];
bool st[N];
int prim()
{
memset(dist, inf, sizeof(dist));
int res = 0;
for(int i = 0; i < n; i ++)
{
int t = -1;
for(int j = 1; j <= n; j ++)
if(!st[j]&&(t == -1||dist[t] > dist[j]))
t = j;
if(i&&dist[t] == inf) return inf;
if(i) res += dist[t];
st[t] = true;
for(int j = 1; j <= n; j ++)
dist[j] = min(dist[j], g[t][j]);
}
return res;
}
Kruskal
时间复杂度:\(O(nlogm)\)
Kruskal
const int N = 1e5 + 10, inf = 0x3f3f3f3f;
struct node
{
int a, b, w;
}s[N * 2];
int fa[N], n, m;
int cmp(node a, node b)
{
return a.w < b.w;
}
void init()
{
for(int i = 1; i <= n; i ++)
fa[i] = i;
}
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int kruskal()
{
sort(s + 1,s + m + 1, cmp);
int res = 0, cnt = 0;
for(int i = 1; i <= m; i ++)
{
int a = s[i].a, b = s[i].b, w = s[i].w;
if(find(a) != find(b))
{
fa[find(a)] = find(b);
cnt ++;
res += w;
}
}
if(cnt == n - 1) return res;
return inf;
}
二分图
染色法判断二分图
染色法判断二分图
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int e[M], ne[M], h[N], color[N], idx;
int n, m;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool dfs(int u, int c)
{
color[u] = c;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!color[j])
{
if(!dfs(j, 3 - c)) return false;
}
else if(color[j] == c)
return false;
}
return true;
}
void solve()
{
memset(h, -1, sizeof(h));
cin >> n >> m;
for(int i = 0; i < m; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
bool flag = true;
for(int i = 1; i <= n; i ++)
{
if(!color[i])
{
if(!dfs(i, 1))
{
flag = false;
break;
}
}
}
if(flag) puts("Yes");
else puts("No");
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return 0;
}
匈牙利算法求最大匹配数
匹配:在图论中,一个「匹配」是一个边的集合,其中任意两条边都没有公共顶点。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替 路称为增广路(\(agumenting\ path\))。
匈牙利算法模板
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 410, M = 1e5 + 10;
int h[N], e[M], ne[M], idx;
int a[N], b[N];
int n, m, q, ans;
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool find(int x)
{
for(int i = h[x]; ~i; i = ne[i])
{
int j = e[i];
if(!st[j])
{
st[j] = true;
if(!b[j]||find(b[j]))
{
b[j] = x;
return true;
}
}
}
return false;
}
void solve()
{
memset(h, -1, sizeof h);
cin >> n >> m >> q;
for(int i = 1; i <= q; i ++)
{
int a, b, c;
cin >> a >> b;
add(a, b);
}
for(int i = 1; i <= n; i ++)
{
memset(st, false, sizeof st);
if(find(i)) ans ++;
}
cout << ans << "\n";
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return 0;
}
拓扑排序
拓扑排序模板
const int N = 100010;
int h[N], e[N], ne[N], idx;
int n, m, q[N], d[N];
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
}
bool topsort()
{
int hh = 0, tt = -1;
for(int i = 1; i <= n; i ++)
if(!d[i])
q[++ tt] = i;
while(hh <= tt)
{
int t = q[hh ++];
for(int i = h[t]; i != -1; i =ne[i])
{
int j = e[i];
d[j] --;
if(d[j] == 0)
q[++ tt] = j;
}
}
return tt == n - 1;
}
强连通分量
连通分量: 对于分量中任意两点 \(u,v\) 必然可以从 \(u\) 走到 \(v\) 且从 \(v\) 走到 \(u\)
强连通分量: 极大连通分量
有向图 → 有向无环图(\(DAG\))
缩点:(将所有连通分量缩成一个点,缩环成点)
应用:求最短/最长路 递推
树枝边、前向边、后向边、横插边
时间戳:\(dfs\)最早遍历到某一点的时间
\(Tarjan\) 算法
求各种连通分量的 \(Tarjan\) 算法,求 \(LCA(Lowest Common Ancestor\),最近公共祖先\()\)的 \(Tarjan\) 算法,并查集、\(Splay、Toptree\) 也是 \(Tarjan\) 发明的。
树枝边\((x,y)\) 中\(dfn[y]>dfn[x],\ low[u]>dfn[u]\)
前向边\((x,y)\) 中\(dfn[y]>dfn[x],\ low[u]>dfn[u]\)
后向边\((x,y)\) 中\(dfn[x]>dfn[y]\), 后向边的终点\(dfn[u] == low[u]\)
横插边\((x,y)\) 中\(dfn[x]>dfn[y]\)
缩点操作后变成有向无环图
就能做 \(topo\) 排序了(此时连通分量编号\(id[]\)递减的顺序就是 \(topo\) 序了)
因为\(++scc_cnt\)是在\(dfs\)完节点i的子节点j后才判断 \(low[u]==dfn[u]\) 后才加的
那么子节点j如果是强连通分量 \(scc_idx[j]\) 一定小于 \(scc_idx[i]\)
Tarjan算法
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt, Size[N];
int dout[N], in[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++timestamp;
stk[++ top] = u, in_stk[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!dfn[j])
{
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if(in_stk[j])
low[u] = min(low[u], dfn[j]);
}
if(dfn[u] == low[u])
{
++ scc_cnt;
int y;
do {
y = stk[top --];
in_stk[y] = false;
id[y] = scc_cnt;
Size[scc_cnt] ++;
}while(y != u);
}
}
有向图的强连通分量
例1. 受欢迎的牛
题目描述:
每一头牛的愿望就是变成一头最受欢迎的牛。
现在有 \(N\) 头牛,编号从 \(1\) 到 \(N\),给你 \(M\) 对整数 \((A,B)\),表示牛 \(A\) 认为牛 \(B\) 受欢迎。
这种关系是具有传递性的,如果 \(A\) 认为 \(B\) 受欢迎,\(B\) 认为 \(C\) 受欢迎,那么牛 \(A\) 也认为牛 \(C\) 受欢迎。
你的任务是求出有多少头牛被除自己之外的所有牛认为是受欢迎的。
输入格式:
第一行两个数 \(N,M\) ;
接下来 \(M\) 行,每行两个数 \(A,B\),意思是 \(A\) 认为 \(B\) 是受欢迎的(给出的信息有可能重复,即有可能出现多个 \(A,B\))。
输出格式
输出被除自己之外的所有牛认为是受欢迎的牛的数量。
输入
3 3
1 2
2 1
2 3
输出
1
数据范围:
\(1≤N≤10^4,1≤M≤5×10^4\)
点击查看代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 1e4 + 10, M = 2e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt, Size[N], dout[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++timestamp;
stk[++ top] = u, in_stk[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!dfn[j])
{
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if(in_stk[j])
low[u] = min(low[u], dfn[j]);
}
if(dfn[u] == low[u])
{
++ scc_cnt;
int y;
do {
y = stk[top --];
in_stk[y] = false;
id[y] = scc_cnt;
Size[scc_cnt] ++;
}while(y != u);
}
}
void solve()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 0; i <m; i ++)
{
int a, b;
cin >> a >> b;
add(a, b);
}
for(int i = 1; i <= n; i ++)
if(!dfn[i])
tarjan(i);
for(int i = 1; i <= n; i ++)
for(int j = h[i]; ~j; j = ne[j])
{
int k = e[j];
int a = id[i], b = id[k];
if(a != b) dout[a] ++;
}
int zero = 0, sum = 0;
for(int i = 1; i <= scc_cnt; i ++)
if(!dout[i])
{
zero ++;
sum += Size[i];
if(zero > 1)
{
sum = 0;
break;
}
}
cout << sum << '\n';
}
signed main()
{
IOS; int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
例2. 学校网络
题目描述:
一些学校连接在一个计算机网络上,学校之间存在软件支援协议,每个学校都有它应支援的学校名单(学校 \(A\) 支援学校 \(B\),并不表示学校 \(B\) 一定要支援学校 \(A\) )。
当某校获得一个新软件时,无论是直接获得还是通过网络获得,该校都应立即将这个软件通过网络传送给它应支援的学校。
因此,一个新软件若想让所有学校都能使用,只需将其提供给一些学校即可。
现在请问最少需要将一个新软件直接提供给多少个学校,才能使软件能够通过网络被传送到所有学校?
最少需要添加几条新的支援关系,使得将一个新软件提供给任何一个学校,其他所有学校就都可以通过网络获得该软件?
输入格式:
第 \(1\) 行包含整数 \(N\),表示学校数量。
第 \(2..N+1\) 行,每行包含一个或多个整数,第 \(i+1\) 行表示学校 \(i\) 应该支援的学校名单,每行最后都有一个 \(0\) 表示名单结束(只有一个 \(0\) 即表示该学校没有需要支援的学校)。
输出格式:
输出两个问题的结果,每个结果占一行。
输入
5
2 4 3 0
4 5 0
0
0
1 0
输出
1
2
数据范围
\(2≤N≤100\)
点击查看代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 1e4 + 10, M = 2e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt, Size[N];
int dout[N], in[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++timestamp;
stk[++ top] = u, in_stk[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!dfn[j])
{
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if(in_stk[j])
low[u] = min(low[u], dfn[j]);
}
if(dfn[u] == low[u])
{
++ scc_cnt;
int y;
do {
y = stk[top --];
in_stk[y] = false;
id[y] = scc_cnt;
Size[scc_cnt] ++;
}while(y != u);
}
}
void solve()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i <= n; i ++)
{
int a, b, x;
while(cin >> a, a) add(i, a);
}
for(int i = 1; i <= n; i ++)
if(!dfn[i])
tarjan(i);
for(int i = 1; i <= n; i ++)
for(int j = h[i]; ~j; j = ne[j])
{
int k = e[j];
int a = id[i], b = id[k];
if(a != b) dout[a] ++, in[b] ++;
}
int p = 0, q = 0;
for(int i = 1; i <= scc_cnt; i ++)
{
if(!dout[i]) p ++;
if(!in[i]) q ++;
}
cout << q << '\n';
if(scc_cnt == 1) p = q = 0;
cout << max(p, q) << '\n';
}
signed main()
{
IOS; int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
例3. 最大半联通子图
题目描述:
一个有向图 \(G=(V,E)\) 称为半连通的 \((Semi-Connected)\),如果满足:\(∀u,v∈V\),满足 \(u→v\) 或 \(v→u\),即对于图中任意两点 \(u,v\),存在一条 \(u\) 到 \(v\) 的有向路径或者从 \(v\) 到 \(u\) 的有向路径。
若 \(G'=(V',E')\) 满足,\(E'\) 是 \(E\) 中所有和 \(V'\) 有关的边,则称 \(G'\) 是 \(G\) 的一个导出子图。
若 \(G'\) 是 \(G\) 的导出子图,且 \(G'\) 半连通,则称 \(G'\) 为 \(G\) 的半连通子图。
若 \(G'\) 是 \(G\) 所有半连通子图中包含节点数最多的,则称 \(G'\) 是 \(G\) 的最大半连通子图。
给定一个有向图 \(G\),请求出 \(G\) 的最大半连通子图拥有的节点数 \(K\),以及不同的最大半连通子图的数目 \(C\)。
由于 \(C\) 可能比较大,仅要求输出 \(C\) 对 \(X\) 的余数。
输入格式:
第一行包含三个整数 \(N,M,X。N,M\) 分别表示图 \(G\) 的点数与边数,\(X\) 的意义如上文所述;
接下来 \(M\) 行,每行两个正整数 \(a,b\),表示一条有向边 \((a,b)\)。
图中的每个点将编号为 \(1\) 到 \(N\),保证输入中同一个 \((a,b)\) 不会出现两次。
输出格式:
应包含两行。
第一行包含一个整数 \(K\),第二行包含整数 \(C mod X\)。
输入
6 6 20070603
1 2
2 1
1 3
2 4
5 6
6 4
输出
3
3
数据范围
\(1≤N≤10^5,1≤M≤10^6,1≤X≤10^8\)
点击查看代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 1e5 + 10, M = 2e6 + 10;
int h[N], hs[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
int scc_cnt, Size[N], id[N];
bool in_stk[N];
int f[N], g[N];
int n, m, x;
void add(int h[], int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++ timestamp;
stk[++ top] = u, in_stk[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!dfn[j])
{
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if(in_stk[j])
low[u] = min(low[u], dfn[j]);
}
if(low[u] == dfn[u])
{
scc_cnt ++;
int y;
do {
y = stk[top --];
in_stk[y] = false;
id[y] = scc_cnt;
Size[scc_cnt] ++;
}while(y != u);
}
}
void solve()
{
memset(h, -1, sizeof h);
memset(hs, -1, sizeof hs);
cin >> n >> m >> x;
for(int i = 0; i < m; i ++)
{
int a, b;
cin >> a >> b;
add(h, a, b);
}
for(int i = 1; i <= n; i ++)
if(!dfn[i])
tarjan(i);
unordered_set<int> se;
for(int i = 1; i <= n; i ++)
{
for(int j = h[i]; ~j; j = ne[j])
{
int k = e[j];
int a = id[i], b = id[k];
int x = a * 1000000ll + b;
if(a != b&&!se.count(x))
{
add(hs, a, b);
se.insert(x);
}
}
}
for(int i = scc_cnt; i; i --)
{
if(!f[i])
{
f[i] = Size[i];
g[i] = 1;
}
for(int j = hs[i]; ~j; j = ne[j])
{
int k = e[j];
if(f[k] < f[i] + Size[k])
{
f[k] = f[i] + Size[k];
g[k] = g[i];
}
else if(f[k] == f[i] + Size[k])
g[k] = (g[k] + g[i]) % x;
}
}
int maxf = 0, sum = 0;
for(int i = 1; i <= scc_cnt; i ++)
{
if(maxf < f[i])
{
maxf = f[i];
sum = g[i];
}
else if(maxf == f[i])
sum = (sum + g[i]) % x;
}
cout << maxf << '\n' << sum << '\n';
}
signed main()
{
IOS; int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
无向图的双连通分量
割点:对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点(又称割顶)。
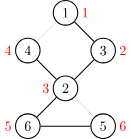
割边:对于一个无向图,如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者割边。严谨来说,就是:假设有连通图 \(G=\{V,E\}\),\(e\) 是其中一条边(即 \(e \in E\)),如果 \(G-e\) 是不连通的,则边 \(e\) 是图 \(G\) 的一条割边(桥)。

在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 \(u\) 和 \(v\) 边双连通。
在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪个点(只能删去一个,且不能删 \(u\) 和 \(v\) 自己)都不能使它们不连通,我们就说 \(u\) 和 \(v\) 点双连通。
边双连通具有传递性,即,若 \(x,y\) 边双连通,\(y,z\) 边双连通,则 \(x,z\) 边双连通。
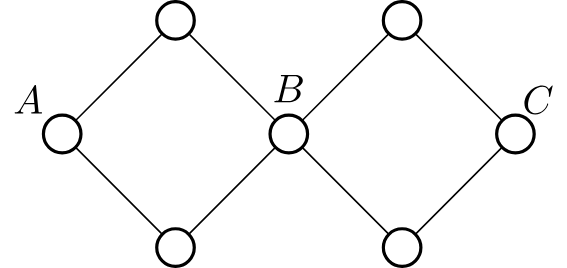
点双连通 不 具有传递性,反例如下图,\(A,B\) 点双连通,\(B,C\) 点双连通,而 \(A,C\) 不 点双连通。

例1. 冗余路径
题目描述:
为了从 \(F\) 个草场中的一个走到另一个,奶牛们有时不得不路过一些她们讨厌的可怕的树。
奶牛们已经厌倦了被迫走某一条路,所以她们想建一些新路,使每一对草场之间都会至少有两条相互分离的路径,这样她们就有多一些选择。
每对草场之间已经有至少一条路径。
给出所有 \(R\) 条双向路的描述,每条路连接了两个不同的草场,请计算最少的新建道路的数量,路径由若干道路首尾相连而成。
两条路径相互分离,是指两条路径没有一条重合的道路。
但是,两条分离的路径上可以有一些相同的草场。
对于同一对草场之间,可能已经有两条不同的道路,你也可以在它们之间再建一条道路,作为另一条不同的道路。
输入格式:
第 \(1\) 行输入 \(F\) 和 \(R\)。
接下来 \(R\) 行,每行输入两个整数,表示两个草场,它们之间有一条道路。
输出格式:
输出一个整数,表示最少的需要新建的道路数。
输入
7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7
输出
2
数据范围:
\(1≤F≤5000,F−1≤R≤10000\)
点击查看代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 1e4 + 10, M = 2e4 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int scc_cnt, id[N];
bool is_bridge[N];
int stk[N], top, d[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void tarjan(int u, int from)
{
dfn[u] = low[u] = ++ timestamp;
stk[++ top] = u;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!dfn[j])
{
tarjan(j, i);
low[u] = min(low[u], low[j]);
if(low[u] < low[j])
is_bridge[i] = is_bridge[i ^ 1] = true;
}
else if(i != (from ^ 1))
low[u] = min(low[u], dfn[j]);
}
if(dfn[u] == low[u])
{
int y;
++ scc_cnt;
do {
y = stk[top --];
id[y] = scc_cnt;
}while(y != u);
}
}
void solve()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 0; i < m; i ++)
{
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
tarjan(1, -1);
for(int i = 0; i < idx; i ++)
if(is_bridge[i])
d[id[e[i]]] ++;
int cnt = 0;
for(int i = 1; i <= scc_cnt; i ++)
if(d[i] == 1)
cnt ++;
cout << (cnt + 1) / 2 << '\n';
}
signed main()
{
IOS; int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
例2. 电力
题目描述:
给定一个由 \(n\) 个点 \(m\) 条边构成的无向图,请你求出该图删除一个点之后,连通块最多有多少。
输入格式:
输入包含多组数据。
每组数据第一行包含两个整数 \(n,m\) 。
接下来 \(m\) 行,每行包含两个整数 \(a,b\),表示 \(a,b\) 两点之间有边连接。
数据保证无重边。
点的编号从 \(0\) 到 \(n−1\)。
读入以一行 \(0\ 0\) 结束。
输出格式:
每组数据输出一个结果,占一行,表示连通块的最大数量。
输入
3 3
0 1
0 2
2 1
4 2
0 1
2 3
3 1
1 0
0 0
输出
1
2
2
数据范围
\(1≤n≤10000,0≤m≤15000,0≤a,b<n\)
点击查看代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 1e4 + 10, M = 3e4 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int root, ans;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++ timestamp;
int cnt = 0;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!dfn[j])
{
tarjan(j);
low[u] = min(low[j], low[u]);
if(dfn[u] <= low[j]) cnt ++;
}
else low[u] = min(low[u], dfn[j]);
}
if(u != root) cnt ++;
ans = max(ans, cnt);
}
void solve()
{
memset(dfn, 0, sizeof dfn);
memset(h, -1, sizeof h);
idx = timestamp = 0;
ans = 0;
int cnt = 0;
for(int i = 0; i < m; i ++)
{
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
for(root = 0; root < n; root ++)
if(!dfn[root])
{
cnt ++;
tarjan(root);
}
cout << ans + cnt - 1 << '\n';
}
signed main()
{
IOS; int _ = 1;
// cin >> _;
while(cin >> n >> m, n||m)
solve();
return _ ^ _;
}
例3. 矿场搭建
题目描述:
煤矿工地可以看成是由隧道连接挖煤点组成的无向图。
为安全起见,希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。
于是矿主决定在某些挖煤点设立救援出口,使得无论哪一个挖煤点坍塌之后,其他挖煤点的工人都有一条道路通向救援出口。
请写一个程序,用来计算至少需要设置几个救援出口,以及不同最少救援出口的设置方案总数。
输入格式:
输入文件有若干组数据,每组数据的第一行是一个正整数 \(N\),表示工地的隧道数。
接下来的 \(N\) 行每行是用空格隔开的两个整数 \(S\) 和 \(T(S≠T)\),表示挖煤点 \(S\) 与挖煤点 \(T\) 由隧道直接连接。
注意,每组数据的挖煤点的编号为 \(1∼Max\),其中 \(Max\) 表示由隧道连接的挖煤点中,编号最大的挖煤点的编号,可能存在没有被隧道连接的挖煤点。
输入数据以 \(0\) 结尾。
输出格式:
每组数据输出结果占一行。
其中第 \(i\) 行以 \(Case\ i:\) 开始(注意大小写,\(Case\) 与 \(i\) 之间有空格,\(i\) 与 \(:\) 之间无空格,\(:\) 之后空格)。
其后是用空格隔开的两个正整数,第一个正整数表示对于第 \(i\) 组输入数据至少需要设置几个救援出口,第二个正整数表示对于第 \(i\) 组输入数据不同最少救援出口的设置方案总数。
输入数据保证答案小于 \(2^{64}\),输出格式参照以下输入输出样例。
输入
9
1 3
4 1
3 5
1 2
2 6
1 5
6 3
1 6
3 2
6
1 2
1 3
2 4
2 5
3 6
3 7
0
输出
Case 1: 2 4
Case 2: 4 1
数据范围
\(1≤N≤500,1≤Max≤1000\)
点击查看代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define ull unsigned long long
using namespace std;
const int N = 1e3 + 10;
int n, m;
int h[N], e[N], ne[N], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
int dcc_cnt;
vector<int> dcc[N];
bool cut[N];
int root;
int _ = 1;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void tarjan(int u)
{
dfn[u] = low[u] = ++ timestamp;
stk[++ top] = u;
if(u == root&&h[u] == -1)
{
dcc_cnt ++;
dcc[dcc_cnt].push_back(u);
return ;
}
int cnt = 0;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(!dfn[j])
{
tarjan(j);
low[u] = min(low[u], low[j]);
if(dfn[u] <= low[j])
{
cnt ++;
if(u != root||cnt > 1) cut[u] = true;
dcc_cnt ++;
int y;
do {
y = stk[top --];
dcc[dcc_cnt].push_back(y);
}while(y != j);
dcc[dcc_cnt].push_back(u);
}
}
else low[u] = min(low[u], dfn[j]);
}
}
void solve()
{
for(int i = 1; i <= dcc_cnt; i ++)
dcc[i].clear();
idx = n = timestamp = top = dcc_cnt = 0;
memset(dfn, 0, sizeof dfn);
memset(h, -1, sizeof h);
memset(cut, 0, sizeof cut);
for(int i = 0; i < m; i ++)
{
int a, b;
cin >> a >> b;
n = max({n, a, b});
add(a, b);
add(b, a);
}
for(root = 1; root <= n; root ++)
if(!dfn[root])
tarjan(root);
int ans = 0;
ull num = 1;
for(int i = 1; i <= dcc_cnt; i ++)
{
int cnt = 0;
for(int j = 0; j < dcc[i].size(); j ++)
if(cut[dcc[i][j]])
cnt ++;
if(cnt == 0)
{
if(dcc[i].size() > 1)
ans += 2, num *= dcc[i].size() * (dcc[i].size() - 1) / 2;
else ans ++;
}
else if(cnt == 1) ans ++, num *= dcc[i].size() - 1;
}
cout << "Case " << _ ++ << ": " << ans << ' ' << num << '\n';
}
signed main()
{
IOS;
// cin >> _;
while(cin >> m, m)
solve();
return _ ^ _;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号