基础算法
目录
排序算法
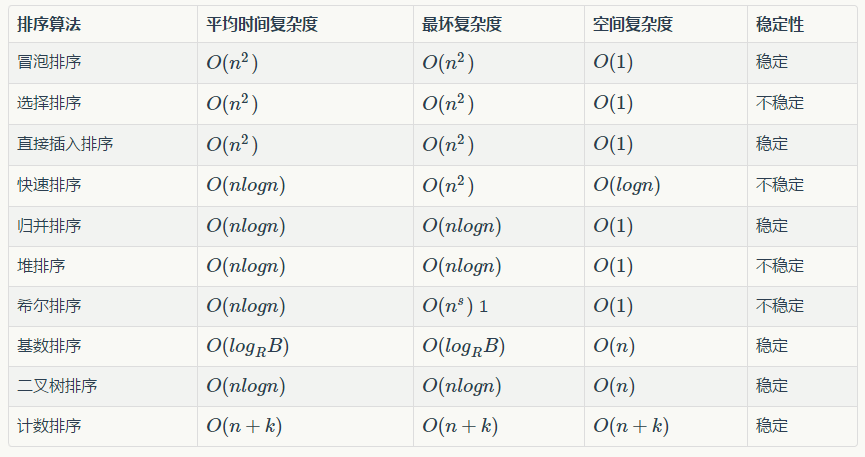
排序算法(英语:Sorting algorithm):是一种将一组特定的数据按某种顺序进行排列的算法。排序算法多种多样,性质也大多不同。
稳定性:稳定性是指相等的元素经过排序之后相对顺序是否发生了改变。
拥有稳定性这一特性的算法会让原本有相等键值的纪录维持相对次序,即如果一个排序算法是稳定的,当有两个相等键值的纪录 \(R\) 和 \(S\),且在原本的列表中 \(R\) 出现在 \(S\) 之前,在排序过的列表中 \(R\) 也将会是在 \(S\) 之前。
时间复杂度:时间复杂度用来衡量一个算法的运行时间和输入规模的关系,通常用 \(O\) 表示。
简单计算复杂度的方法一般是统计「简单操作」的执行次数,有时候也可以直接数循环的层数来近似估计。
基于比较的排序算法的时间复杂度下限是 \(O(n\log n)\) 的。
当然也有不是 \(O(n\log n)\) 的。例如,计数排序 的时间复杂度是 \(O(n+w)\),其中 \(w\) 代表输入数据的值域大小。
选择排序
选择排序(英语:\(Selection sort)\)是一种简单直观的排序算法。它的工作原理是每次找出第 \(i\) 小的元素(也就是 \(A\_{i..n}\) 中最小的元素),然后将这个元素与数组第 \(i\) 个位置上的元素交换。
稳定性:不稳定
由于 \(swap\)(交换两个元素)操作的存在,选择排序是一种不稳定的排序算法。
时间复杂度:选择排序的最优时间复杂度、平均时间复杂度和最坏时间复杂度均为 \(O(n^2)\)。
选择排序
void selection_sort(int a[], int n)
{
for(int i = 1; i < n; i ++)
{
int t = i;
for(int j = i + 1; j <= n; j ++)
if(a[j] < a[t])
t = j;
swap(a[i], a[t]);
}
}
冒泡排序
冒泡排序(英语:\(Bubble\ sort\)):是一种简单的排序算法。由于在算法的执行过程中,较小的元素像是气泡般慢慢「浮」到数列的顶端,故叫做冒泡排序。它的工作原理是每次检查相邻两个元素,如果前面的元素与后面的元素满足给定的排序条件,就将相邻两个元素交换。当没有相邻的元素需要交换时,排序就完成了。
经过 \(i\) 次扫描后,数列的末尾 \(i\) 项必然是最大的 \(i\) 项,因此冒泡排序最多需要扫描 \(n-1\) 遍数组就能完成排序。
稳定性:稳定
时间复杂度:冒泡排序的平均时间复杂度为 \(O(n^2)\)。
冒泡排序
void bubble_sort(int a[], int n)
{
bool f = true;
while(f)
{
f = false;
for(int i = 1; i < n; i ++)
{
if(a[i] > a[i + 1])
{
f = true;
swap(a[i], a[i + 1]);
}
}
}
}
插入排序
插入排序(英语:\(Insertion\ sort\))是一种简单直观的排序算法。它的工作原理为将待排列元素划分为「已排序」和「未排序」两部分,每次从「未排序的」元素中选择一个插入到「已排序的」元素中的正确位置。
稳定性:稳定
时间复杂度:插入排序的最坏时间复杂度和平均时间复杂度都为 \(O(n^2)\)。
插入排序
void insertion_sort(int a[], int n)
{
for(int i = 1; i < n; i ++)
{
int t = a[i], j = i - 1;
while(j >= 0&&a[j] > t)
a[j + 1] = a[j], j --;
a[j + 1] = t;
}
}
优化--折半插入排序
void inssertion_sort(int a[], int n)
{
if(n < 2) return ;
for(int i = 1; i != n; i ++)
{
int t = a[i];
auto j = upper_bound(a, a + i, t) - a;
memmove(a + j + 1, a + j, (i - j) * sizeof(int));
a[j] = t;
}
}
计数排序
计数排序(英语:\(Counting\ sort\))是一种线性时间的排序算法。工作原理是使用一个额外的数组 $C,其中第 \(i\) 个元素是待排序数组 \(A\) 中值等于 \(i\) 的元素的个数,然后根据数组 C 来将 \(A\) 中的元素排到正确的位置。
过程工作:
1.计算每个数出现了几次;
2.求出每个数出现次数的 前缀和;
3.利用出现次数的前缀和,从右至左计算每个数的排名。
稳定性:稳定
时间复杂度:计数排序的时间复杂度为 \(O(n+w)\),其中 \(w\) 代表待排序数据的值域大小。
点击查看代码
void counting_sort(int a[], int n)
{
int b[100010], s[100010];
memset(s, 0, sizeof s);
for(int i = 1; i <= n; i ++)
s[a[i]] ++;
for(int i = 1; i <= 100000; i ++)
s[i] += s[i - 1];
for(int i = n; i >= 1; i --)
b[s[a[i]] --] = a[i];
}
快速排序
快速排序(英语:\(Quicksort\)),又称分区交换排序(英语:partition-exchange sort),简称「快排」,是一种被广泛运用的排序算法。
快速排序的工作原理是通过 分治 的方式来将一个数组排序。
1.将数列划分为两部分(要求保证相对大小关系);
2.递归到两个子序列中分别进行快速排序;
3.不用合并,因为此时数列已经完全有序。
稳定性:不稳定
时间复杂度:\(O(nlogn)\)
点击查看代码
void quick_sort(int a[], int l, int r)
{
if(l >= r) return ;
int x = a[(l+r+1)/2], i = l - 1, j = r + 1;
while(i < j)
{
while(a[++ i] < x);
while(a[-- j] > x);
if(i < j) swap(a[i], a[j]);
}
quick_sort(a, l, i - 1);
quick_sort(a, i, r);
}
归并排序
归并排序(\(merge\ sort\))是高效的基于比较的稳定排序算法。
稳定性:稳定
时间复杂度:\(O(logn)\)
高精度
加法
加法
void solve()
{
string aa, bb;
int a[N], b[N], c[N];
cin >> aa >> bb;
int la = aa.size(), lb = bb.size(), mx = max(la, lb);
for(int i = 0; i < la; i ++) a[la - i - 1] = aa[i] - '0';
for(int i = 0; i < lb; i ++) b[lb - i - 1] = bb[i] - '0';
for(int i = 0; i < mx; i ++)
{
c[i] += a[i] + b[i];
if(c[i] > 9)
c[i + 1] ++, c[i] -= 10;
}
while(!c[mx]&&mx >= 1) mx --;
while(mx >= 0)
printf("%d", c[mx --]);
}
减法
减法
void solve()
{
string aa, bb;
int a[N], b[N], c[N];
cin >> aa >> bb;
int la = aa.size(), lb = bb.size(), mx = max(la, lb);
for(int i = 0; i < la; i ++) a[la - i - 1] = aa[i] - '0';
for(int i = 0; i < lb; i ++) b[lb - i - 1] = bb[i] - '0';
for(int i = 0; i < mx; i ++)
{
c[i] += a[i] - b[i];
if(c[i] < 0)
c[i + 1] --, c[i] += 10;
}
if(c[mx] < 0)
{
cout << '-';
for(int i = 0; i <= mx; i ++) c[i] = 0;
for(int i = 0; i < mx; i ++)
{
c[i] += b[i] - a[i];
if(c[i] < 0)
c[i + 1] --, c[i] += 10;
}
}
while(!c[mx]&&mx >= 1) mx --;
while(mx >= 0) cout << c[mx --];
}
乘法
乘法vector
vector<int > mul(vector<int> a, int b, int x)
{
int t = 0;
vector<int> c;
reverse(c.begin(), c.end());
for(int i = 0; i < a.size()||t; i ++)
{
if(i < a.size())
t += a[i] * b;
if(!i) t += x;
c.push_back(t % 10);
t /= 10;
}
while(!c.back() && c.size() > 1)
c.pop_back();
// reverse(c.begin(), c.end());
return c;
}
乘法数组
void solve()
{
char aa[N];
int a[N], b, c[N], n;
cin >> aa >> b;
n = strlen(aa);
for(int i = 0; i < n; i ++)
a[n - i - 1] = aa[i] - 48;
int mx = 0, t = 0, i;
for(i = 0; i < n||t; i ++)
{
if(i < n) t += a[i] * b;
c[i] = t % 10;
t /= 10;
}
while(!c[i]&&i > 0) i --;
for(i; i >= 0; i --)
cout << c[i];
}
除法
除法vector
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
vector<int> div(vector<int> &A, int &B, int &r)
{
vector<int> C;
for(int i = 0; i < A.size(); i ++)
{
r = r * 10 + A[i];
C.push_back(r / B);
r %= B;
}
reverse(C.begin(), C.end());
while(C.size() > 1&&C.back() == 0) C.pop_back();
return C;
}
int main()
{
vector<int> A;
string a;
int B, r = 0;
cin >> a >> B;
for(int i = 0; i < a.size(); i ++) A.push_back(a[i] - '0');
auto C = div(A, B, r);
for(int i = C.size() - 1; i >= 0; i --)
cout << C[i];
cout << endl << r << endl;
return 0;
}
除法数组
void solve()
{
char aa[N];
int a[N], b, r, c[N], cnt;
cin >> aa >> b;
int n = strlen(aa);
for(int i = 0; i < n; i ++)
a[i] = aa[i] - 48;
int i;
for(i = 0; i < n; i ++)
{
r = r * 10 + a[i];
c[cnt ++] = r / b;
r %= b;
}
reverse(c, c + cnt);
while(!c[cnt]&&cnt > 0) cnt --;
for(cnt; cnt >= 0; cnt --)
cout << c[cnt];
cout << endl << r;
}
前缀和 + 差分
一维前缀和
一维前缀和
void solve()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
sum[i] = sum[i - 1] + a[i];
}
for(int i = 1; i <= m; i ++)
{
cin >> l >> r;
cout << sum[r] - sum[l - 1] << '\n';
}
}
二维前缀和(子矩阵的和)
二维前缀和
void solve()
{
cin >> n >> m >> q;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
{
cin >> a[i][j];
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i] [j];
}
while(q --)
{
int x1, x2, y1, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] << '\n';
}
}
一维差分
一维差分
void solve()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
b[i] = a[i] - a[i - 1];
}
int l, r, c;
for(int i = 1; i <= m; i ++)
{
cin >> l >> r >> c;
b[l] += c, b[r + 1] -= c;
}
for(int i = 1; i <= n; i ++)
b[i] += b[i - 1];
for(int i = 1; i <= n; i ++)
cout << b[i] << ' ';
}
二维差分(差分矩阵)
二维差分
void solve()
{
int n, m, q;
cin >> n >> m >> q;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
{
cin >> a[i][j];
b[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1];
}
while(q --)
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
b[x1][y1] += c, b[x1][y2+1] -= c;
b[x2+1][y1] -= c, b[x2+1][y2+1] += c;
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= m; j ++)
cout << a[i][j] << ' ';
cout << '\n';
}
}
二分
二分查找(英语:\(binary\ search\)),也称折半搜索(英语:\(half-interval\ search\))、对数搜索(英语:\(logarithmic\ search\)),是用来在一个有序数组中查找某一元素的算法。
时间复杂度:\(O(logn)\)
找最左边
int lerfen(int x)
{
int l = 1, r = n, m;
while(l < r)
{
m = l + r >> 1;
if(a[m] >= x) r = m;
else l = m + 1;
}
return l;
}
找最右边
int rerfen(int x)
{
int l = 1, r = n, m;
while(l < r)
{
m = l + r + 1 >> 1;
if(a[m] <= x) l = m;
else l = m - 1;
}
return r;
}
小数二分
void solve()
{
int n;
cin >> n;
auto erfen = [&](double x)
{
return x * x * x;
};
double l = -1e4, r = 1e4, m;
while(r - l >= 1e-7)
{
m = (l + r) / 2.0;
if(erfen(m) >= n) r = m;
else l = m;
}
cout << fixed << setprecision(6) << l;
}
双指针
倍增
倍增法(英语:\(binary\ lifting\)),顾名思义就是翻倍。它能够使线性的处理转化为对数级的处理,大大地优化时间复杂度。
这个方法在很多算法中均有应用,最常用的是 \(RMQ\) 问题和求 \(LCA\)(最近公共祖先)。
RMQ
\(RMQ\) 是英文 \(Range\ Maximum/Minimum\ Query\) 的缩写,表示区间最大(最小)值。
默认初始数组大小为 \(n\),询问次数为 \(m\)。
\(RMQ\) 可以在 \(nlogn\) 的时间下完成f数组的建立,下边是区间最大值的查询,对于区间\([l,r]\),存在一个 \(k\) 使得 \(r-l+1>=2^k\) 且 \(r-l+1<2^{(k+1)}\) ,这样的话区间 \([l,r]\) 的最大值就是 \(max(f[l,k],f[r-2^k+1,k])\) ,查询可以在常数级完成。
倍增法求RMQ
点击查看代码
void init_RMQ()
{
for(int j = 0; j < M; j ++)
for(int i = 1; i + (1 << j) - 1 <= n; i ++)
if(!j) mn[i][j] = a[i];
else mn[i][j] = max(mn[i][j - 1], mn[(i + (1 << j - 1))][j - 1]);
}
int RMQ(int l, int r)
{
int k = r - l + 1;
k = log(k) / log(2);
return max(mn[l][k], mn[r - (1 << k) + 1][k]);
}
例.天才的记忆
题目描述
从前有个人名叫 \(WNB\),他有着天才般的记忆力,他珍藏了许多许多的宝藏。
在他离世之后留给后人一个难题(专门考验记忆力的啊!),如果谁能轻松回答出这个问题,便可以继承他的宝藏。
题目是这样的:给你一大串数字(编号为 \(1\) 到 \(N\),大小可不一定哦!),在你看过一遍之后,它便消失在你面前,随后问题就出现了,给你 \(M\) 个询问,每次询问就给你两个数字 \(A,B\),要求你瞬间就说出属于 \(A\) 到 \(B\) 这段区间内的最大数。
一天,一位美丽的姐姐从天上飞过,看到这个问题,感到很有意思(主要是据说那个宝藏里面藏着一种美容水,喝了可以让这美丽的姐姐更加迷人),于是她就竭尽全力想解决这个问题。
但是,她每次都以失败告终,因为这数字的个数是在太多了!
于是她请天才的你帮他解决。如果你帮她解决了这个问题,可是会得到很多甜头的哦!
输入格式
第一行一个整数 \(N\) 表示数字的个数。
接下来一行为 \(N\) 个数,表示数字序列。
第三行读入一个 \(M\),表示你看完那串数后需要被提问的次数。
接下来 \(M\) 行,每行都有两个整数 \(A,B\)。
输出格式
输出共 \(M\) 行,每行输出一个数,表示对一个问题的回答。
输入
6
34 1 8 123 3 2
4
1 2
1 5
3 4
2 3
输出
34
123
123
8
数据范围
\(1≤N≤2×10^5,1≤M≤10^4,1≤A≤B≤N\)。
点击查看代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N = 2e5 + 10, M = 20;
int mn[N][M];
int a[N];
int n, m;
void init()
{
for(int j = 0; j < M; j ++)
for(int i = 1; i + (1 << j) - 1 <= n; i ++)
if(!j) mn[i][j] = a[i];
else mn[i][j] = max(mn[i][j - 1], mn[(i + (1 << j - 1))][j - 1]);
}
int RMQ(int l, int r)
{
int k = r - l + 1;
k = log(k) / log(2);
return max(mn[l][k], mn[r - (1 << k) + 1][k]);
}
void solve()
{
cin >> n;
for(int i = 1; i <= n; i ++)
cin >> a[i];
init();
cin >> m;
while(m --)
{
int l, r;
cin >> l >> r;
cout << RMQ(l, r) << "\n";
}
}
int main()
{
IOS;
int T = 1;
while(T --)
solve();
return T ^ T;
}
LCA
倍增法求LCA
点击查看代码
void LCA_init()
{
int hh = 0, tt = -1;
ce[root] = 1;
q[++ tt] = root;
while(hh <= tt)
{
int t = q[hh ++];
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(ce[j] == 0)
{
ce[j] = ce[t] + 1;
dist[j] = dist[t] + w[i];
q[++ tt] = j;
fa[j][0] = t;
for(int k = 1; k < 15; k ++)
fa[j][k] = fa[fa[j][k - 1]][k - 1];
}
}
}
}
int LCA(int a, int b)
{
if(ce[a] < ce[b]) swap(a, b);
for(int i = 14; i >= 0; i --)
if(ce[fa[a][i]] >= ce[b])
a = fa[a][i];
if(a == b) return a;
for(int i = 14; i >= 0; i --)
if(fa[a][i] != fa[b][i])
{
a = fa[a][i];
b = fa[b][i];
}
return fa[a][0];
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号