动态规划--DP
目录
动态规划
动态规划是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
背包
01背包
每个物体只有两种可能的状态(取与不取),对应二进制中的 \(0\) 和 \(1\),这类问题便被称为「0-1 背包问题」。
状态转移方程:
这里如果直接采用二维数组,有多余空间浪费
由于每个物品只有选或不选两种情况,即最多选一次,故可从体积出发逆向枚举每个物品
时间复杂度:\(O(n\times v)\)
点击查看代码
for(int i = 1; i <= n; i ++)
{
for(int j = m; j >= v[i]; j --)
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
}
完全背包
完全背包模型与 \(0-1\) 背包类似,与 \(0-1\) 背包的区别仅在于一个物品可以选取无限次,而非仅能选取一次。
虑一个朴素的做法:对于第 i 件物品,枚举其选了多少个来转移。这样做的时间复杂度是 \(O(n^3)\) 的。
状态转移方程如下:
考虑做一个简单的优化。可以发现,对于 \(f_{i,j}\),只要通过 \(f_{i,j-w_i}\) 转移就可以了。因此状态转移方程为:
时间复杂度:\(O(n\times v)\)
理由是当我们这样转
每个物品可选无数次,故可以从体积出发正向枚举每个合法的物品
点击查看代码
for(int i = 1; i <= n; i ++)
{
for(int j = v[i]; j <= m; j ++)
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
}
多重背包
多重背包也是 \(0-1\) 背包的一个变式。与 \(0-1\) 背包的区别在于每种物品有 \(k_i\) 个,而非一个。
一个很朴素的想法就是:把「每种物品选 \(k_i\) 次」等价转换为「有 \(k_i\) 个相同的物品,每个物品选一次」。这样就转换成了一个 \(0-1\) 背包模型,套用上文所述的方法就可已解决。状态转移方程如下:
时间复杂度 \(O(W\sum_{i=1}^nk_i)\)。
点击查看代码
for(int i = 1; i <= n; i ++)
{
for(int j = 0; j <= m; j ++)
{
for(int k = 0; k <= s[i]&&k * v[i] <= j; k ++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + w[i] * k);
}
}
混合背包
混合背包就是将前面三种的背包问题混合起来,有的只能取一次,有的能取无限次,有的只能取 \(k\) 次。
按照背包种类分类求解,求最优解
例. 混合背包问题
题目描述:
有 N 种物品和一个容量是 V 的背包。
物品一共有三类:
·第一类物 品只能用\(1\)次(\(01\)背包);
·第二类物品可以用无限次(完全背包);
·第三类物品最多只能用 \(s_i\) 次(多重背包);每种体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式:
第一行两个整数,\(N,V\),用空格隔开,分别表示物品种数和背包容积。
接下来有 \(N\) 行,每行三个整数 \(v_i,w_i,s_i\),用空格隔开,分别表示第 i 种物品的体积、价值和数量。
·\(s_i=−1\) 表示第 \(i\) 种物品只能用1次;
·\(s_i=0\) 表示第 \(i\) 种物品可以用无限次;
·\(s_i>0\) 表示第 \(i\) 种物品可以使用 \(s_i\)次;
输出格式:
输出一个整数,表示最大价值。
输入
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
输出
8
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 1e3 + 10;
int v[N], w[N], s[N], f[N];
int n, m;
void solve()
{
cin >> n >> m;
for(int i = 0; i < n; i ++)
{
cin >> w[i] >> v[i] >> s[i];
if(!s[i])
for(int j = w[i]; j <= m; j ++)
f[j] = max(f[j], f[j - w[i]] + v[i]);
else
{
if(s[i] == -1) s[i] = 1;
for(int k = 1; k <= s[i]; k *= 2)
{
for(int j = m; j >= k * w[i]; j --)
f[j] = max(f[j], f[j - k * w[i]] + k * v[i]);
s[i] -= k;
}
if(s[i])
for(int j = m; j >= s[i] * w[i]; j --)
f[j] = max(f[j], f[j - s[i] * w[i]] + s[i] * v[i]);
}
}
cout << f[m] << endl;
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
二进制优化
具体地说就是令 \(A_{i,j}\left(j\in\left[0,\lfloor \log_2(k_i+1)\rfloor-1\right]\right)\) 分别表示由 \(2^{j}\) 个单个物品「捆绑」而成的大物品。特殊地,若 \(k_i+1\) 不是 \(2\) 的整数次幂,则需要在最后添加一个由 \(k_i-2^{\lfloor \log_2(k_i+1)\rfloor-1}\) 个单个物品「捆绑」而成的大物品用于补足。
将每种物品按照上述方式拆分后,使用 0-1 背包的方法解决即可。
时间复杂度: \(O(W\sum_{i=1}^n\log_2k_i)\)
点击查看代码
for(int i = 1; i <= n; i ++)
{
cin >> w >> v >> s;
int k = 1;
while(s > k)
{
s -= k;
p[cnt ++] = {w * k, v * k};
k *= 2;
}
p[cnt ++] = {w * s, v * s};
}
for(int i = 0; i < cnt; i ++)
for(int j = m; j >= p[i].w; j --)
f[j] = max(f[j], f[j - p[i].w] + p[i].v);
单调队列优化
点击查看代码
for(int i = 1; i <= n; i ++)
{
for(int r = 0; r < v[i]; r ++)
{
int hh = 0, tt = -1;
for(int j = r; j <= m; j += v[i])
{
while(hh <= tt&&j - q[hh] > v[i] * s[i]) hh ++;
while(hh <= tt&&f[(i - 1) & 1][q[tt]] + (j - q[tt]) / v[i] * w[i] <= f[(i - 1) & 1][j]) tt --;
q[++ tt] = j;
f[i & 1][j] = f[(i - 1) & 1][q[hh]] + (j - q[hh]) / v[i] * w[i];
}
}
}
二维费用背包
和 \(0-1\) 背包问题类似,不同的是选一个物品会消耗两种价值(经费、时间),可对每种价值进行\(0-1\)背包
点击查看代码
for(int i = 0; i < n; i ++)
{
for(int j = V; j >= v[i]; j --)
{
for(int l = W; l >= w[i]; l --)
f[j][l] = max(f[j][l], f[j - v[i]][l - w[i]] + a[i]);
}
}
分组背包
从「在所有物品中选择一件」变成了「从当前组中选择一件」,可对每一组进行一次 \(0-1\) 背包。
点击查看代码
for(int i = 1; i <= n; i ++)
{
for(int j = m; j >= 0; j --)
{
for(int k = 1; k <= s[i]; k ++)
if(j >= v[i][k])
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
有依赖的背包
考虑分类讨论。对于一个主件和它的若干附件,有以下几种可能:只买主件,买主件 + 某些附件。因为这几种可能性只能选一种,所以可以将这看成分组背包。
如果是多叉树的集合,则要先算子节点的集合,最后算父节点的集合。
例. 有依赖的背包问题
题目描述:
有 \(N\) 个物品和一个容量是 \(V\) 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示: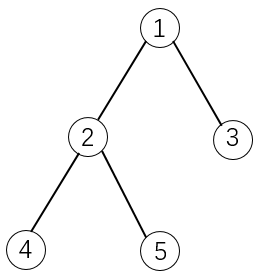
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 \(i\),体积是 \(v_i\),价值是 \(w_i\),依赖的父节点编号是 \(p_i\)。物品的下标范围是 \(1…N\)。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式:
第一行有两个整数 \(N,V\),用空格隔开,分别表示物品个数和背包容量。
接下来有 \(N\) 行数据,每行数据表示一个物品。第 \(i\) 行有三个整数 \(v_i,w_i,p_i\),用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 \(p_i=−1\),表示根节点。 数据保证所有物品构成一棵树。
输出格式:
输出一个整数,表示最大价值。
输入
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
输出
11
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 110;
vector<int> g[N];
int f[N][N];
int v[N], w[N];
int n, m, root;
void dfs(int x)
{
for(int i = v[x]; i <= m; i ++)
f[x][i] = w[x];
for(int i = 0; i < g[x].size(); i ++)
{
int y = g[x][i];
dfs(y);
for(int j = m; j >= v[x]; j --)
{
for(int k = 0; k <= j - v[x]; k ++)
f[x][j] = max(f[x][j], f[x][j - k] + f[y][k]);
}
}
}
void solve()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
{
int fa;
cin >> v[i] >> w[i] >> fa;
if(fa == -1) root = i;
else
g[fa].push_back(i);
}
dfs(root);
cout << f[root][m] << "\n";
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
泛化物品的背包
这种背包,没有固定的费用和价值,它的价值是随着分配给它的费用而定。在背包容量为 \(V\) 的背包问题中,当分配给它的费用为 \(v_i\) 时,能得到的价值就是 \(h\left(v_i\right)\)。这时,将固定的价值换成函数的引用即可。
杂项
根据贪心原理,当费用相同时,只需保留价值最高的;当价值一定时,只需保留费用最低的;当有两件物品 \(i,j\) 且 \(i\) 的价值大于 \(j\) 的价值并且 \(i\) 的费用小于 \(j\) 的费用时,只需保留 \(i\)。
背包问题变种
输出方案其实就是记录下来背包中的某一个状态是怎么推出来的。我们可以用 \(g_{i,v}\) 表示第 \(i\) 件物品占用空间为 \(v\) 的时候是否选择了此物品。然后在转移时记录是选用了哪一种策略(选或不选)。
求方案数
对于给定的一个背包容量、物品费用、其他关系等的问题,求装到一定容量的方案总数。
这种问题就是把求最大值换成求和即可。
例如 \(0-1\) 背包问题的转移方程就变成了:
初始条件:\(\mathit{dp}_0=1\)
因为当容量为 \(0\) 时也有一个方案,即什么都不装。
例1. 背包问题求方案数
题目描述:
有 \(N\) 件物品和一个容量是 \(V\) 的背包。每件物品只能使用一次。
第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 \(10^9+7\) 的结果。
输入格式:
第一行两个整数,\(N,V\),用空格隔开,分别表示物品数量和背包容积。
接下来有 \(N\) 行,每行两个整数 \(v_i,w_i\),用空格隔开,分别表示第 \(i\) 件物品的体积和价值。
输出格式:
输出一个整数,表示 方案数 模 \(10_9+7\) 的结果。
输入
4 5
1 2
2 4
3 4
4 6
输出
2
数据范围
\(0<N,V≤1000\)
\(0<v_i,w_i≤1000\)
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
#define mod 1000000007
using namespace std;
const int N = 1010;
int f[N], g[N];
int n, m;
void solve()
{
cin >> n >> m;
for(int i = 0; i <= m; i ++) g[i] = 1;
for(int i = 1; i <= n; i ++)
{
int v, w;
cin >> v >> w;
for(int j = m; j >= v; j --)
{
if(f[j] < f[j - v] + w)
{
f[j] = f[j - v] + w;
g[j] = g[j - v];
}
else if(f[j] == f[j - v] + w)
g[j] = (g[j - v] + g[j]) % mod;
}
}
cout << g[m] << "\n";
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
例2. 跑步
题目描述:
路人甲准备跑 n 圈来锻炼自己的身体,他准备分多次(>1)跑完,每次都跑正整数圈,然后休息下再继续跑。
为了有效地提高自己的体能,他决定每次跑的圈数都必须比上次跑的多。
可以假设他刚开始跑了 \(0\) 圈,那么请问他可以有多少种跑完这 \(n\) 圈的方案?
输入格式:
一行一个整数,代表 \(n\)。
输出格式:
一个整数表示跑完这 \(n\) 圈的方案数。
输入
212
输出
995645335
数据范围
对于 \(100%\) 的数据,保证 \(5≤n≤500\)。
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 510;
int n, m;
void solve()
{
cin >> n;
vector<int> f(n + 1, 0);
f[0] = 1;
for(int i = 1; i <= n; i ++)
for(int j = n; j >= i; j --)
f[j] += f[j - i];
cout << f[n] - 1 << '\n';
}
signed main()
{
IOS; int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
线性DP
指状态之间有线性关系的动态规划问题。
数字三角形
例1. 数字三角形
题目描述:
给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
7 3 88 1 0
2 7 4 4
4 5 2 6 5
输入格式:
第一行包含整数 \(n\),表示数字三角形的层数。
接下来 \(n\) 行,每行包含若干整数,其中第 \(i\) 行表示数字三角形第 \(i\) 层包含的整数。
输出格式:
输出一个整数,表示最大的路径数字和。
输入
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出
30
数据范围
\(1≤n≤500\),
\(−10000≤\)三角形中的整数\(≤10000\)
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 510;
int f[N][N], n;
void solve()
{
cin >> n;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= i; j ++)
cin >> f[i][j];
for(int i = n - 1; i >= 1; i --)
for(int j = i; j >= 1; j --)
f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + f[i][j];
cout << f[1][1] << "\n";
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
例2. 最短编辑距离
题目描述:
给定两个字符串 \(A\) 和 \(B\),现在要将 \(A\) 经过若干操作变为 \(B\),可进行的操作有:
·删除–将字符串 \(A\) 中的某个字符删除。
·插入–在字符串 \(A\) 的某个位置插入某个字符。
·替换–将字符串 \(A\) 中的某个字符替换为另一个字符。
现在请你求出,将 \(A\) 变为 \(B\) 至少需要进行多少次操作。
输入格式:
第一行包含整数 \(n\),表示字符串 \(A\) 的长度。
第二行包含一个长度为 \(n\) 的字符串 \(A\)。
第三行包含整数 \(m\),表示字符串 \(B\) 的长度。
第四行包含一个长度为 \(m\) 的字符串 \(B\)。
字符串中均只包含大小写字母。
输出格式:
输出一个整数,表示最少操作次数。
输入
10
AGTCTGACGC
11
AGTAAGTAGGC
输出
4
数据范围
\(1≤n,m≤1000\)
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 1010;
int f[N][N];
char a[N], b[N];
int n, m;
void solve()
{
cin >> n >> a + 1 >> m >> b + 1;
for(int i = 0; i <= n; i ++)
f[i][0] = i;
for(int i = 0; i <= m; i ++)
f[0][i] = i;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
{
f[i][j] = min(f[i][j - 1], f[i - 1][j]) + 1;
f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
}
cout << f[n][m] << endl;
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
最长上升子序列
例. 最长上升子序列 II
题目描述:
给定一个长度为 \(N\) 的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式:
第一行包含整数 \(N\) 。
第二行包含 \(N\) 个整数,表示完整序列。
输入
7
3 1 2 1 8 5 6
输出
4
数据范围
\(1≤N≤100000\) ,
\(−10^9≤数列中的数≤10^9\)
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 1e5 + 10;
int n, a[N], f[N];
void solve()
{
cin >> n;
for(int i = 0; i < n; i ++)
cin >> a[i];
int len = 0;
for(int i = 0; i < n; i ++)
{
int l = 0, r = len;
while(l < r)
{
int m = l + r + 1 >> 1;
if(f[m] < a[i]) l = m;
else r = m - 1;
}
f[r + 1] = a[i];
if(r + 1 > len) len ++;
}
cout << len << endl;
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
状态机
例1. 大盗阿福
题目描述:
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 \(N\) 家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式:
输入的第一行是一个整数 \(T\),表示一共有 \(T\) 组数据。
接下来的每组数据,第一行是一个整数 \(N\) ,表示一共有 \(N\) 家店铺。
第二行是 \(N\) 个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过\(1000\)。
输出格式:
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
输入
2
3
1 8 2
4
10 7 6 14
输出
8
24
数据范围
\(1≤T≤50 ,1≤N≤10^5\)
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 1e5 + 10;
int t, n, w;
int f[N];
void solve()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> t;
while(t --)
{
cin >> n;
cin >> f[1];
for(int i = 2; i <= n; i ++)
{
cin >> w;
f[i] = max(f[i - 1], f[i - 2] + w);
}
cout << f[n] << "\n";
}
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
例2. 设计密码
题目描述:
你现在需要设计一个密码 \(S,S\) 需要满足:
·\(S\) 的长度是 \(N\);
·\(S\) 只包含小写英文字母;
·\(S\) 不包含子串 \(T\);
例如:\(abc\) 和 \(abcde\) 是 \(abcde\) 的子串 \(abd\) 不是 \(abcde\)的子串。
请问共有多少种不同的密码满足要求?
由于答案会非常大,请输出答案模 \(10^9+7\)
的余数。
输入格式:
第一行输入整数 \(N\),表示密码的长度。
第二行输入字符串 \(T,T\) 中只包含小写字母。
输出格式:
输出一个正整数,表示总方案数模 \(10^9+7\)
后的结果。
输入1
2
a
输出1
625
输入2
4
cbc
输出2
456924
数据范围
\(1≤N≤50,1≤|T|≤N\),\(|T|\)是\(T\)的长度。
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 60, mod = 1e9 + 7;
int ne[N], f[N][N];
char s[N];
int ans, n, m;
void solve()
{
cin >> n >> (s + 1);
m = strlen(s + 1);
for(int i = 2, j = 0; i <= m; i ++)
{
while(j&&s[i] != s[j + 1]) j = ne[j];
if(s[i] == s[j + 1]) j ++;
ne[i] = j;
}
f[0][0] = 1;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
for(char k = 'a'; k <= 'z'; k ++)
{
int u = j;
while(u&&k != s[u + 1]) u = ne[u];
if(k == s[u + 1]) u ++;
if(u < m) f[i + 1][u] = (f[i + 1][u] + f[i][j]) % mod;
}
for(int i = 0; i < m; i ++)
ans = (ans + f[n][i]) % mod;
cout << ans << "\n";
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
例3. 股票买卖 V
题目描述:
给定一个长度为 \(N\) 的数组,数组中的第 \(i\) 个数字表示一个给定股票在第 \(i\) 天的价格。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
·你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
·卖出股票后,你无法在第二天买入股票 (即冷冻期为 \(1\) 天)。
输入格式:
第一行包含整数 \(N\),表示数组长度。
第二行包含 \(N\) 个不超过 \(10000\) 的正整数,表示完整的数组。
输出格式:
输出一个整数,表示最大利润。
输入
5
1 2 3 0 2
输出
3
数据范围
\(1≤N≤10^5\)
解释
对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出],第一笔交易可得利润 \(2-1 = 1\),第二笔交易可得利润 \(2-0 = 2\),共得利润 \(1+2 = 3\)。
点击查看代码
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
#define int long long
using namespace std;
const int N = 1e5 + 10;
int n, a[N], f[N][3];
void solve()
{
cin >> n;
for(int i = 1; i <= n; i ++)
cin >> a[i];
memset(f, -0x3f, sizeof f);
f[0][0] = 0;
for(int i = 1; i <= n; i ++)
{
f[i][0] = max(f[i - 1][0], f[i - 1][2]);
f[i][1] = max(f[i - 1][1], f[i - 1][0] - a[i]);
f[i][2] = f[i - 1][1] + a[i];
}
cout << max(f[n][0], f[n][2]) << "\n";
}
signed main()
{
IOS;
int _ = 1;
// cin >> _;
while(_ --)
solve();
return _ ^ _;
}
例4. 最大子段和
题目描述:
给出一个长度为 \(n\) 的序列 \(a\),选出其中连续且非空的一段使得这段和最大。
输入格式:
第一行是一个整数,表示序列的长度 \(n\)。
第二行有 \(n\) 个整数,第 \(i\) 个整数表示序列的第 \(i\) 个数字 \(a_i\) 。
输出格式:
输出一行一个整数表示答案。
输入
7
2 -4 3 -1 2 -4 3
输出
4
数据范围
对于 \(40\%\) 的数据,保证 \(n≤2×10 3\) 。
对于 \(100\%\) 的数据,保证 \(1≤n≤2×10^5 ,−10^4 ≤a_i ≤10^4\) 。
点击查看代码
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr)
// #define int long long
using namespace std;
const int N = 1e6 + 10, inf = 1e10;
int n, m, ans, t;
int f[N][2], a[N];
void solve()
{
ans = -inf;
cin >> n;
for(int i = 1; i <= n; i ++)
cin >> a[i], t = t | (a[i] > 0);
if(!t)
{
for(int i = 1; i <= n; i ++)
ans = max(ans, a[i]);
}
else
for(int i = 1; i <= n; i ++)
{
if(a[i] < 0)
{
f[i][0] = max(f[i - 1][1], max(f[i - 1][0], 0));
f[i][1] = max(f[i - 1][1] + a[i], a[i]);
}
else
{
f[i][0] = max(f[i - 1][1], max(f[i - 1][0], 0));
f[i][1] = max(f[i - 1][1] + a[i], a[i]);
}
ans = max(f[i][0], f[i][1]);
}
cout << ans << '\n';
}
signed main()
{
IOS; int _ = 1;
// cin >> n;
while(_ --)
solve();
return _ ^ _;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号