B树和B+树

1. B树是什么

　　相比较与二叉树，B树就是一种多分树，它的子节点可以大于二叉，主要应用于静态索引数据，它是AVL树的进化版，B树的左节点比父节点小，右节点比父节点大。

　　1. 定义

　　　　1. 每个结点最多只有m个子结点（m值B树的阶）

　　　　2. 除根节点外，每个非叶子结点最少有m/2个子结点

　　　　3. 非叶子节点的根节点至少有两个子节点

　　　　4. 有m阶B树的最多有m-1个键，键按照递增顺序排列

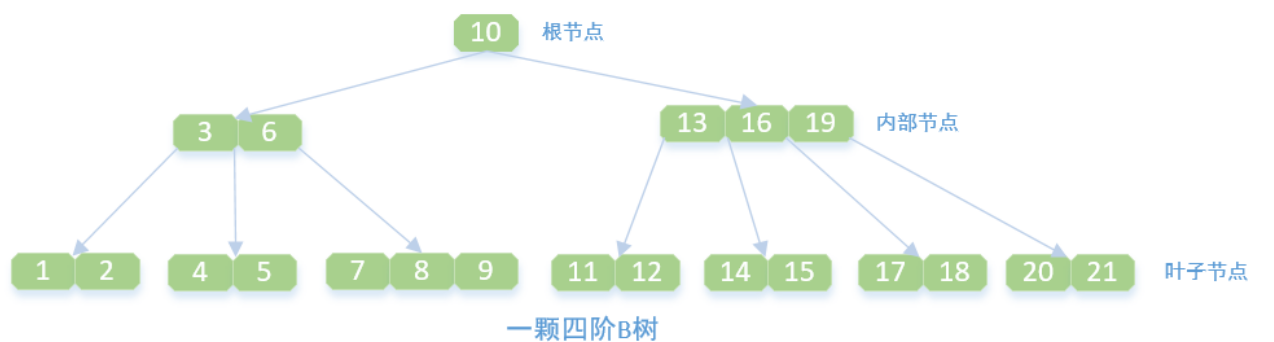
　　　如图所示：一个4阶的B树

　　    

　　　　

• • B树的阶　　　　　

 　　　　　　B树中一个节点的子节点的最大值，如图 [13,16,19] 节点的子节点为4，所以是4阶

• • 根节点

　　　　　　B树中最顶的那个节点，如果根节点不是唯一节点，那么它至少有两个子节点

• • 树的键

　　　　　　即树的关键字，如[13,16,19] 节点13,16,19就是键

 

2. B树的查找，插入和删除

　　1. 查找

　　　　B树的查找会根据关键字key从根部到叶子节点逐层进行，通过二分法检索，如果key=某个节点，则查找成功；如果在某两个节点之间，则在该子节点上继续查找，重复进行，如果到叶子节点还没有匹配上，说明不存在这个key。他的时间复杂度和树的深度成正比。

 

　　2. 插入

　　　　当往一颗B树中插入新的节点时，首先对该B树进行查询，不存在则进行插入，插入的规则如下：

• • 若该节点元素小于m-1时，直接插入该节点
  • 若该节点元素等于m-1时，则进行分裂，以该节点中间的元素作为该节点的父元素进行分裂

　　　　以一颗5阶的B树为例

　　　　（1） 当B树的叶子节点中元素为m-1时，往其中插入53

　　　　

 

　　　　（2） 在往其中插入13,21,40

　　　　

 

 　　　　（3）依次插入30、27、 33 

　　　　

 

 　　　　（4）依次插入36、35、34； 24、29

　　　　

 

 　　　　

　　　　（5）依次插入24、29

　　　　

 

 

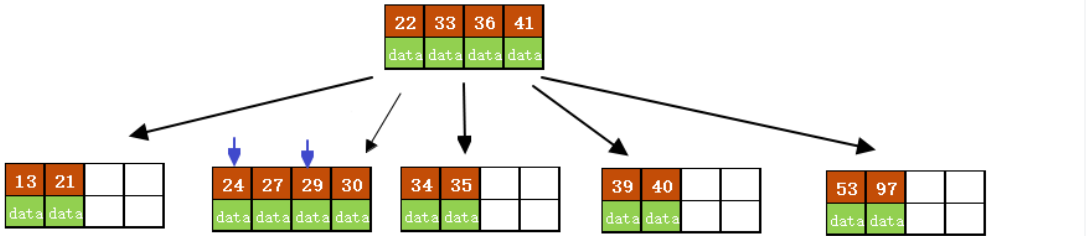
　　　　（6）插入26

　　　　

 

 

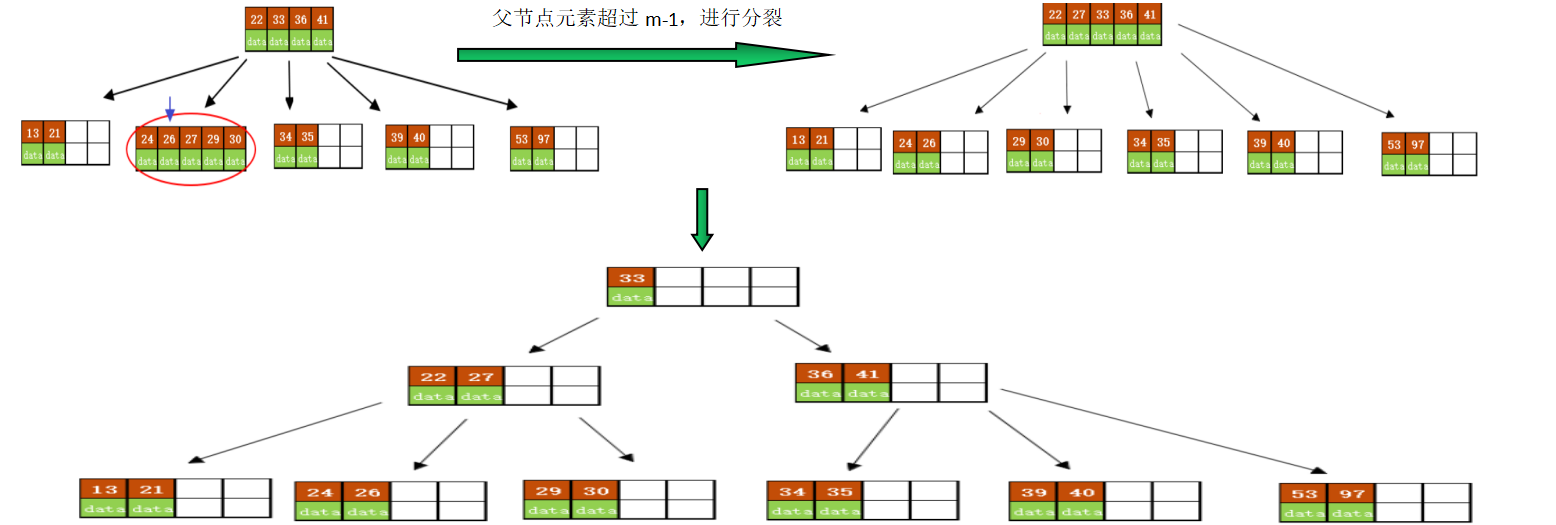
 　　3. 删除

　　　　删除B树中的元素，首先需要对该元素进行查找，删除该元素后，会对该树进行调整，如果该树不存在子节点，则无需调整；如果该树存在左右子节点，则将左孩子的最右元素或者右孩子的最左元素移动到父节点中；

• • 如果某一节点元素中的个数小于（m / 2）-1时，向上取整，则父节点的一颗key移动到该节点，兄弟节点上移父节点
  • 如果该结点key个数大于等于(m/2)-1，结束删除操作

　　　　以一颗5阶的B树为例

　　　　（1）删除8后，该节点的元素数量不小于m/2-1，无需调整

　　　　

 

 

　　　　（2）删除20，该节点非叶子节点且数量小于m/2-1，需要调整

　　　　

 

 

　　　　（3）删除18后，该叶子节点的数量小于m/2-1，父节点移动元素到该节点，再从兄弟节点移动元素到父节点

　　　　

 

 　　

　　　　（4）删除5

　　　　

 

 

 

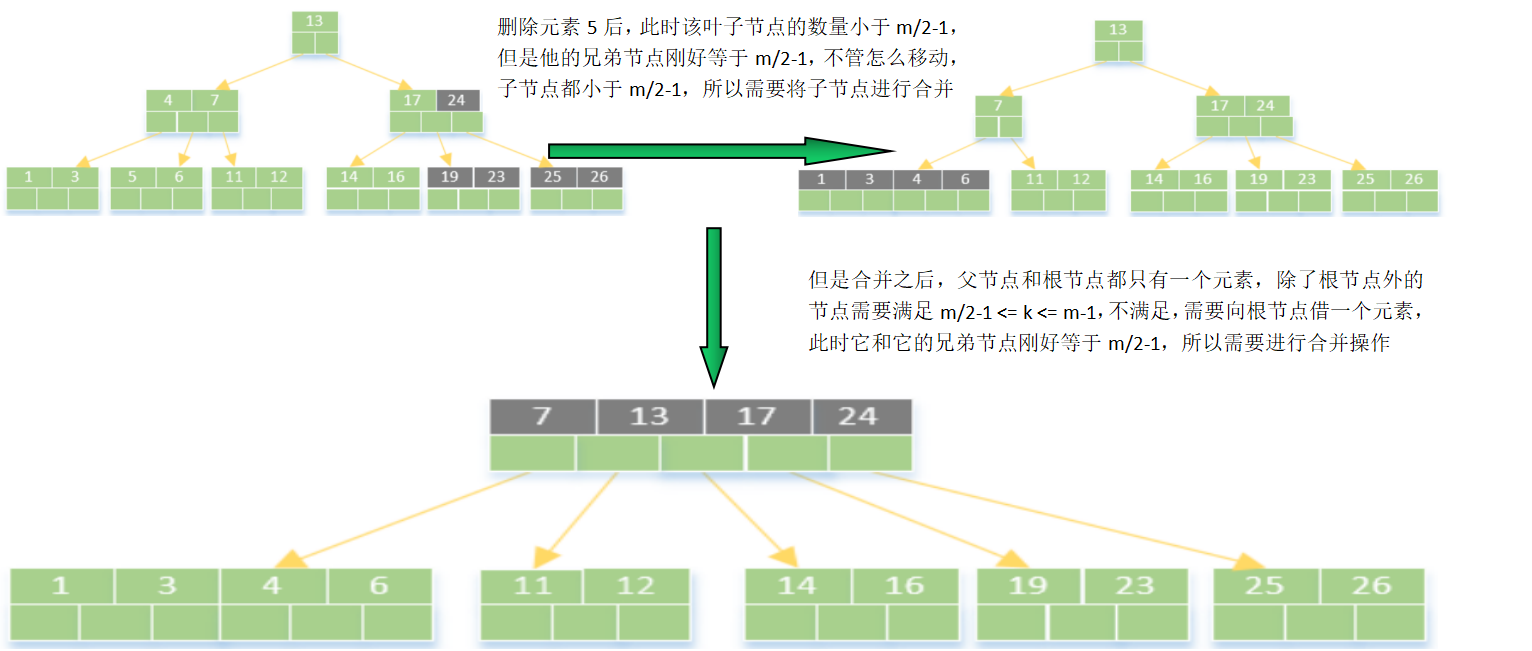
3. B+树

　　1. 定义

　　　　B+树是根据B树演变而来，一颗m阶B+树满足以下条件

• • 每个节点最多只有m个子结点
  • 除根节点外，每个非叶子节点至少有m/2（向下）个子结点
  • 非叶子节点的根节点至少有2个子节点
  • 有k棵子树的非叶子节点有k个键
  • 叶节点都在同一层中

 　　　　

 

 　　

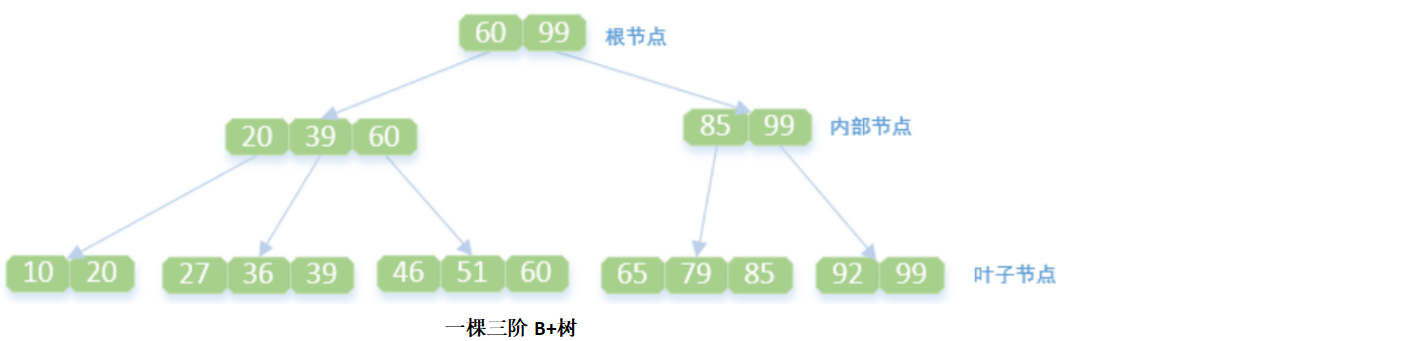
　　2. B+树的查找、插入和删除

　　　1. 查找

　　　　在B+树中检索关键码key的方法与B树的检索方式相似，但若在内部节点中找到检索的关键码时并不会结束搜索，要继续找到B+树的叶子结点为止

　　　2. 插入

　　　　与B树的插入操作相似，总是插到叶子结点上。当叶节点中原关键码的个数等于m时，该节点分裂成两个节点，分别使关键码的个数为 (m+1)/2 （向上取整）和 (m+1)/2 （向下取整）

　　　3. 删除

　　　　仅在叶节点删除关键码，若因为删除操作使得节点中关键码数少于 m/2（向下取整）时，则需要调整或者和兄弟节点合并。合并的过程和B树类似，区别是父节点中作为分界的关键码不放入合并后的节点中。

 

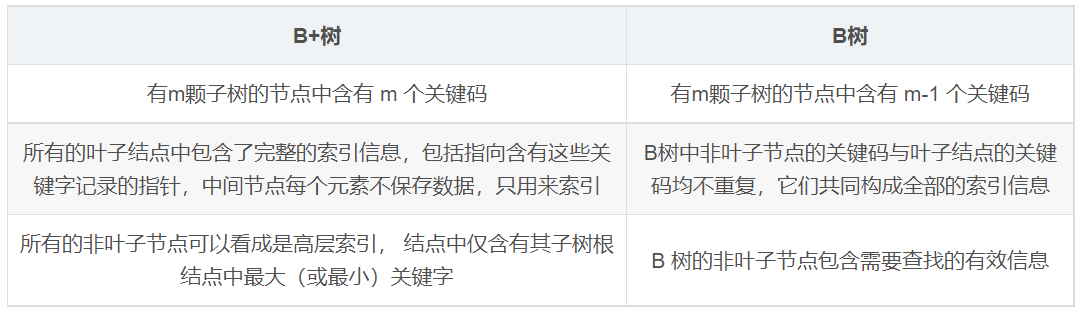
4. B树和B+树的区别